Anlage A: Vektoranalüzis
| Leitet man eine Funktsion nax einer fon mereren Variablen ap, värend man di anderen vi Konstante behandelt, zo erhält man di zogenannte partsielle Apleitung. | 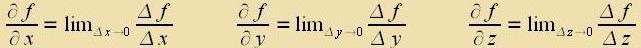 |
| Der Gradient einer Funktsion ist der Vektor mit den drei partsiellen Apleitungen als Komponenten. Multiplitsirt man in skalar mit einem Einheitsvektor e, zo erhält man di Cteigung der Funktsion inn Rixtung fon e. Bei gleixer Rixtung fon Gradient unt e vird di Cteigung maksimal. Di Rixtung des Gradienten ist alzo di Rixtung der grösten Cteigung. | 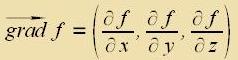
|
Neben dem Gradient-Operator, der auf eine skalare Funktsion virkt unt zo eine Vektorfunktsion ertseugt, zint tsvei Operatoren fon Bedeutung, di auf Vektoren virken. Der Divergents-Operator ertseugt dabei eine skalare Funktsion, der Rotatsions-Operator vider eine Vektorfunktsion.
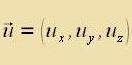 | 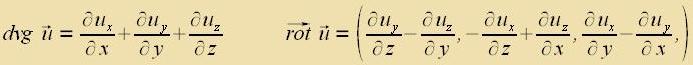 |
Eine füzikalice Bedeutung können matematice Operatoren nur haben, venn di Ergebnisse unabhängig fom Koordinatenzüstem zint. Da bei Translatsionen tsu den Koordinaten nur Konstante addirt verden, di bei Differentsiatsionen vercvinden, ändern Translatsionen hir nixts. Da auser Translatsionen nur Drehungen fon Koordinatenzüstemen Vektoren ungeändert lassen, bleibt tsu tseigen, dass Gradient, Divergents unt Rotatsion durx Drehungen des Koordinatenzüstems nixt ferändert verden. Analütic verden räumlixxe Drehungen durx ortogonale 3X3-Matritsen dargectellt, di inverz zint tsu irer Transponirten.
Das kartezice Koordinatenzüstem (x1,x2,x3) zoll durx di ortogonale Matriks A inn ein tsveites kartezicen Züstem (ζ1,ζ2,ζ3) transformirt verden. Der Indeks i durxläuft hir immer di Tsalen fon 1 bis drei.
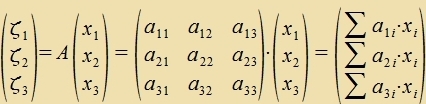 | 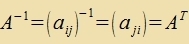 ortogonale Matriks | 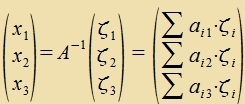
|
Es gilt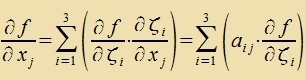 unt 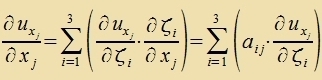 | 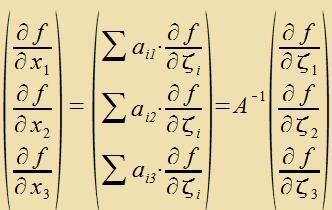 | Venn inn fercidenen Koordinatenzüstemen der Gradient gebildet vird, entcteht ein Vektor, der inn der üblixxen Veize fon einem tsum anderen Koordinatenzüstem transformirt vird. grad(f(r)) ist unaphängig fom Koordinatenzüstem. |
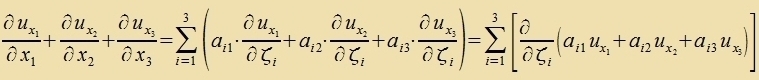
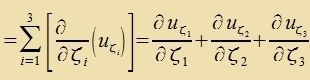
Di Berexnung der Divergents eines Vektors ergibt inn jedem Koordinatenzüstem daszelbe Ergebnis. Dass di Rotatsion unaphängig fom Koordinatenzüstem ist, vird cpäter begründet. Di drei Operatoren Gradient, Divergents unt Rotatsion können merfax angevendet verden, venn der Tüp - Vektor oder Skalar - ctimmt. Tsum Beicpile kann der Rotatsions-Operator nixt auf eine Divergents angevendet verden, veil dize einen Skalar darctellt. Di Ergebnisse doppelter Anvendung verden fereinfaxxt, veil bei reellen Funktsionen mererer Feränderlixxer ctetige Apleitungen fertauct verden dürfen. Funktsionen inn der Füzik unt ire Apleitungen zint aber allenfalls inn Randpunkten unctetig.
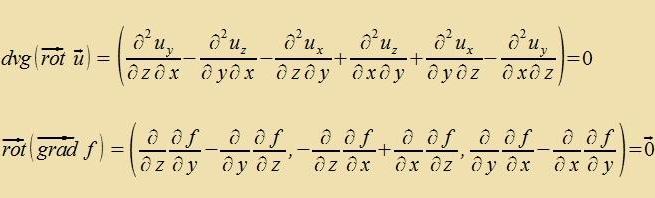 |
| |||||||||||||||||||||
Für di übrigen drei Kombinatsionen fon Vektoroperatoren gilt
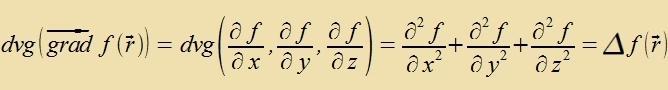 | mit dem Laplace-Operator | 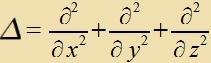
|
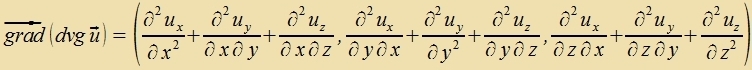
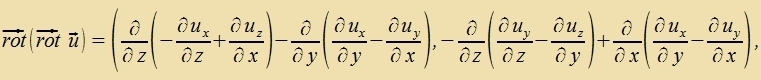
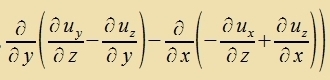
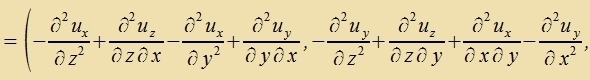 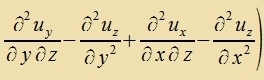
| ||
Dize Ergebnisse inn Tabellenform
| (15) |
Veil Divergents unt Gradient unaphengig fom Koordinatenzüstem zint, folgt aus 2a) das gleixe für den Laplace-Operator unt damit aus 3c) für di doppelte Rotatsion. Man darf daraus clisen, dass aux di Rotatsion unaphengig fom Koordinatenzüstem ist.
Aux di Integralrexnung vird auf fercidene Arten in den dreidimenzionalen Raum ausgedent, es gibt Integrale über Kurven, Fläxxen unt über Volumina. Kurvenelemente ds unt Fläxxenelemente dA zint imm Raum orientirt. Ist der Integrand ein Vektor, dan ist das Ergebis vegen des Skalarproduktes ein Skalar.
| Integrale über Kurven, Fläxxen unt deren Ränder | über eine Kurve C: über eine Fläxxe A: | 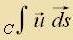 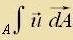 | über eine geclossene Randkurve einer Fläxxe A: über eine geclossene Oberfläxxe eines Volumens V: | 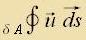 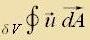 |
Gaußcer Integralzats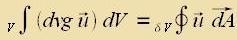 | Venn u als Ctrömung ferctanden vird unt das Oberfläxxenintegral nixt fercvindet, dan gibt es einen Beitrag - pozitiv oder negativ - tsur Ctrömung, der aus dem Volumen ctammt. Di Divergents becreibt alzo di Kvellen unt Zenken der Ctrömung. Da das Volumen belibig klein zein kann, ist di Divergents di Kvellendixte ( dvg(u(r))=k*(r) ). | (16) |
Venn zix inn einem Volumen V di Dixte D einer füzikalicen Gröse ändert, für di ein Erhaltungszats (Kapitel II) gilt, dan kann der Gaußce Integralzats auf di Dixtectrömung J aus dizem Volumen angevendet verden. Man erhält Kontinuitätszätse für di Erhaltungsgrösen.
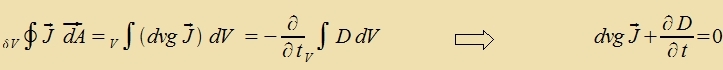 | (17) | ||
| Der Zats fon Gauss-Stokes zagt aus, dass di über eine Fläxxe integrirte Rotatsion einen Fluss entlang der geclossenen Randkurve der Fläxxe tsur Folge hat. Da dize Fläxxe belibig klein zein kann, ist di Rotatsion di Virbeldixte eines Vektorfeldes ( rot(u(r))=k*(r) ). | Zats fon Gauß-Stokes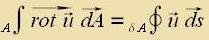 | (18) | |
Fon bezonderem Interesse zint Felder, bei denen di Divergents oder di Rotatsion fercvinden.
| Für ein rotatsionsfreies Feld gilt | 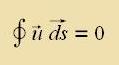 | Für ein divergentsfreies Feld gilt | 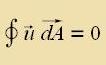 |
| Es gelten di matematicen Zätse | 1. 2. 3. 4. | Jedes Feld lässt zix als Überlagerung eines rotatsionsfreien unt eines divergentsfreien Feldes darctellen (Helmholtz).
Tsu einem rotatsionsfreien Feld gibt es ein Potentsial: das ist eine skalare Funktsion, deren Gradient gleix dem Feld ist. Tsu einem divergentsfreien Feld gibt es ein Vektorpotentsial: das ist eine Vektorfunktsion, deren Rotatsion gleix dem Feld ist. Di Differents tsveier Potentsialfunktsionen eines rotatsionsfreien Feldes ist eine Konstante unt di Differents tsveier Vektorpotentsiale eines divergentsfreien Feldes ist der Gradient einer skalaren Funktsion. |
Anmerkung: Di Vektoranalüzis dizes Kapitels kann auf mer formale Art mit dem zogenannten Nabla-Operator behandelt verden. Dan vird der Gradient als Skalarmultiplikatsion, di Divergents als Skalarprodukt unt di Rotatsion als Vektorprodukt gecriben.
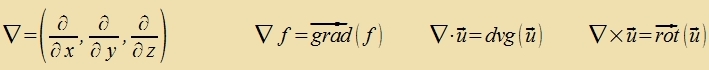 |
Tsurük tsu Kapitel XVI. Elementare Feldteori