Füzik

Home

XVI. Elementare Feldteori

Porträ (bearbeitet) Fundctelle

	Zeit alten Tseiten beobaxteten di Mencen fastsinirt, vi ein Mangnet one erkennbare Ferbindung über eine Entfernung auf einen anderen Mangneten virkt. Newton ferctand als erster, dass ein zo alltäglixxer Forgang vi der fallende Apfel auf Gravitatsion beruht unt dass dize Gravitatsion eine änlixxe Fernvirkung ist vi di mangnetice. Allerdings hilt con Newton es für apzurd, dass Massen zix one irgendeine Ferbindung tsviccen inen antsihen zollten, unt zo entctand bei der Becreibung der elektromangneticen Vekselvirkungen der Begriff des Feldes: Jedem Punkt des Raumes verden Eigencaften tsugecriben, unt di Feldteori unterzuxt Funtsionen (Skalare) unt Vektorfuntsionen imm dreidimenzionalen Raum. Di Entdekkung immer neuer Elementarteilxen, irer Vekselvirkungen bis hin tsur Enctehung unt Fernixtung fürte imm letsten Jarhundert tsu einigen veiteren Feldern, zodas heute di Felder gleixgevixtig neben der Materie ctehen. Di unaphengige Variable bei einer skalaren oder vektoriellen Feldfunktsion ist ein Punkt r imm dreidimenzionalen Raum. Auf dize Feldfunktsionen verden drei Vektor-Operatoren angevendet: di Divergents (dvg), der Gradient (grad) unt di Rotatsion (rot). Datsu kommen Integratsionen über Volumina, Fläxxen unt Kurven imm Raum. Etvas fon der Matematik, das imm folgenden tsur Analüze fon Feldfunktsionen benötigt vird, ist imm Anhang tsu finden. Di elektrice Ladung ist eine Erhaltungsgröse (II). Daher gilt für di Ladungsdixte ρ unt di Ctromdixte j di Kontinuitätsgleixung (Gl. (17) imm Anhang) Venn zix inn einem Punkt imm Raum di Ladungsdixte ändert, entcteht dort ein Beitrag tsur Ctromdixte unt dizer Beitrag ist gleix der tseitlixxen Änderung der Ladungsdixte. Imm Gravitatsionsfeld G(r) ist di Arbeit unaphengig fom Veg, das Gravitatsionsfeld ist rotatsionsfrei unt kann als Gradient einer Potentsialfunktsion ΦG(r) dargectellt verden. Di Kvellen des Gravitatsionsfelds zint Massen, di Kvellendixte d∗(r) ist bis auf eine Konstante gleix der Massendixte. Da der Gradient inn Rixtung der ctärksten Tsuname des Potentsials tseigt, virkt das Gravitatsionsfeld G(r) genau entgegengezetst. Es gilt (fgl. (15)) Aux imm elektricen Feld E(r) ist di Arbeit unaphengig fom Veg, E kann ebenfalls als Gradient einer skalaren Funktsion ΦE(r) dargectellt verden. Venn konventsionell inn Analogi tsur Gravitatsion der negative Gradient gevält vird, becreibt das Feld den Fall der Antsihung tsviccen elektricen Ladungen. Di Ladungsdixte ρ(r) unt damit aux di Kvelldixte ρ*(r) eines Feldes E, das eine pozitive Ladung q antsiht, muss daher negativ zein. Es gilt (fgl. (15)) Das ctatsionäre Mangnetfeld ist divergentsfrei, da es keine mangneticen Monopole gibt. B(r) kann daher als Rotatsion eines Vektorpotentsials A(r) dargectellt verden. Venn das Mangnetfeld durx Ctröme ferurzaxxt vird, ist di Virbeldixte j∗(r) bis auf einen konstanten Faktor gleix der elektricen Ctromdixte.	(1) (2) (3) (4)
	Veil di Rotatsion eines Gradienten fercvindet (Gl. 3a inn Tabelle A15) ist di Funktsion f(r) folgenloz für das Mangnetfeld, zi ist frei välbar. Dize Freiheit (Eixfreiheit) vird genutst, um das Vektorpotentsial für di jeveilige Anvendung antsupassen, tsu eixen. Um den Ausdrukk für di Virbeldixte tsu fereinfaxxen, zoll das Vektorpotentsial jetst zo geeixt verden, dass di Divergents fercvindet. Tsu einem imm Printsip bekannten, aber nixt geeixten Vektorpotentsial Au(r) findet man das geeixte über di Gleixung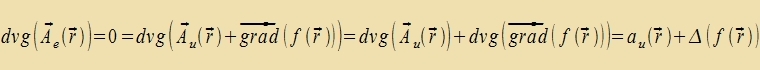 Dis ist eine Differentsialgleixung tsveiter Ordnung für di Funktsion f(r) mit der imm Printsip bekannten Funktsion au(r). Zi ist lözbar, muss hir aber nixt gelözt verden. Es reixt tsu vissen, dass es ein entcprexxend geeixtes Vektorpotentsial gibt. Mit der Eixung vird unt Für jedes der drei Felder G(r), E(r) unt B(r) gibt es eine Konstante, di tsviccen dem Feld unt der Dixte der ferurzaxxenden Gröse fermittelt. Di drei Konstanten zint historic auf zer untercidlixxe Veize entdekkt unt gemessen vorden. Inn dizem teoreticen Kapitel können zi nur an der rixtigen Ctelle eingezetst verden, di Becreibung irer eksperimentellen Bectimmung folgt inn den näxsten Kapiteln. 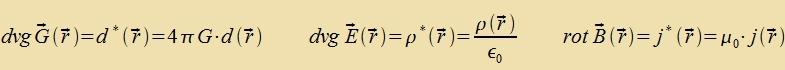Damit gelten tsviccen den Dixten d, ρ unt j, den Feldern unt Potentsialen di Betsihungen 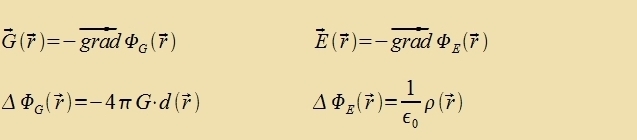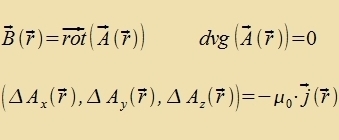Venn eine Kugel K mit konstanter Massendixte d fon einer gröseren kontsentricen Kugel V mit dem Radius r, inn der es keine veiteren Massen gibt, eingeclossen vird, dan folgt aus dem Gaußcen Integralzats 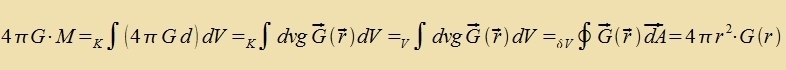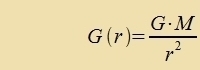Vegen F(r)=m∙G(r) ist das Gravitatsionsfeld der Kugelmasse M das Becleunigungsfeld für eine tsveite Masse m. Für eine elektric homogen geladene Kugel folgt inn gleixer Veize 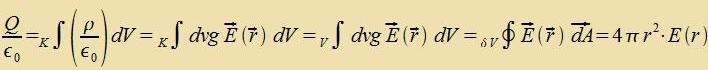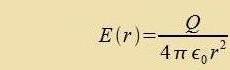Venn eine Kreizfläxxe F mit konstanter Virbeldixte fon einem gröseren Kreiz mit dem Radius r, der kontsentric inn der gleixen Ebene ligt unt inn dem es keine veitere Virbeldixte gibt, umgeben vird, dan folgt aus dem Zats fon Gauß-Stokes 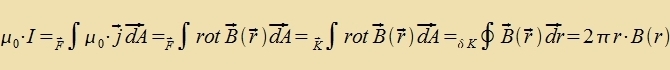Veil der Ctrom zenkrext tsur Ebene der beiden Kreize flisen zoll unt das Feld entlang der Periferi des gröseren Kreizes ferläuft, ist das Feld (12) zenkrext tsum Ctrom unt tsum Radiusvektor. Di Felder (10) unt (11) zint rotatsionszümmetric.	(6) (7) (8) (9) (10)   (11)   (12)
	Gravitatsionsfeld einer Kugel der Masse M Elektrices Feld einer Kugelladung Q Mangnetfeld eines geraden Ctromes I Das Gravitatsionspotentsial einer Masse ist unt für di Antsihungskraft tsveier Masse gilt das Gravitatsionsgezets Das elektroctatice Potentsial einer Ladung ist Das Coulombce Gezets becreibt di Kraft tsviccen tsvei Ladungen	(13)   (14)   (15)
	Di Figur tseigt einen Cnitt durx den Mittelpunkt einer kugelzümmetrice Anordnung mit einer dünnen Kugelcale (rot), auf der eine Gezamtladung Q gleixmäsig verteilt ist. Veil es innerhalb der inneren Kugel keine Ladung gibt, ist dort dvgE=0 unt nax Gleixung (11) fercvindet das Integral für E dA über die Oberfläxxe dizer Kugel. Veil aus Gründen der Zümmetri E dA überall auf der Oberfläxxe der Kugel den gleixen Vert hat, kann E dort nur gleix Null zein. Daszelbe gilt für den gezamten Innenraum der geladenen Kugelcale. Auf der Oberfläxxe der äuseren Kugel mit dem Radius r gilt nax Gleixung (11) E(r)=Q/(4πr2ε0). Di Entfernung der geladenen Kugelcale fom Mittelpunkt oder fon der äuseren Kugel maxxt dabei keinen Untercid, di Ladung kann aux eine Punktladung imm Mittelpunkt der Anordnung zein. Mit einer Masse M ctat der Ladung Q fürt di gleixe Überlegung tsum entcprexxenden Ergebnsis. Innerhalb einer auf einer Kugelcale gleixmäsig ferteilten Masse M gibt es kein Gravitatsionsfeld unt das Gravitatsionsfeld einer zolxen Massenferteilung ist auserhalb das gleixe vi das der Masse M im Mittelpunkt der Kugelcale. Ist d(r) eine kugelzümmetrice Massenferteilung, dan virkt auf eine Masse m inn der Entfernung R fom Zümmetritsentrum nur di Gezamtmasse innerhalb der Kugel mit dem Radius R. mit	(16)
A