FLRW-Metrik und Friedmann-Gleichungen |
| In der dreidimensionalen Hyperebene | 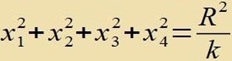 | des ℝ4 wird das Element | 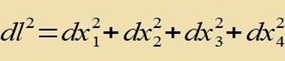 | umgeschrieben in r, φ,θ |
| mit den Koordinatentransformationen | 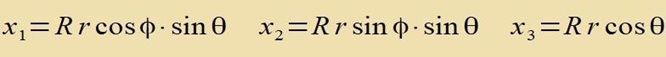
| Man erhält zunächst für die dxi |
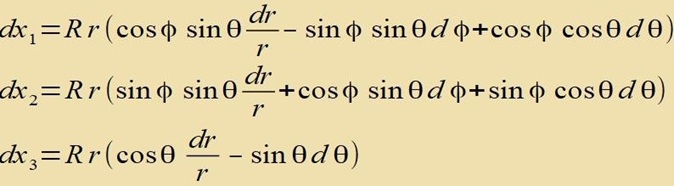 | Wenn die Quadrate der dxi addiert werden, heben sich alle gemischten Glieder dr⋅dφ, dφ⋅dθ und dθ⋅dr gegenseitig auf. Es bleibt 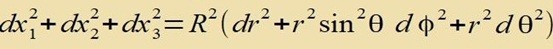
|
| Mit | 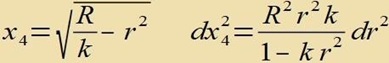 | folgt schließlich | 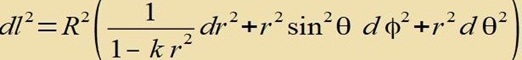
|
| Das Linienelement wird nun gebildet aus zeitlichem und räumlichem Anteil | 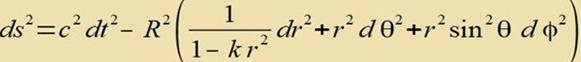
|
Der Parameter R, der für die räumliche Größe des Universums steht, ist wegen dessen Expansion nicht konstant und muss als zeitliche Funktion a(t) eingesetzt werden.
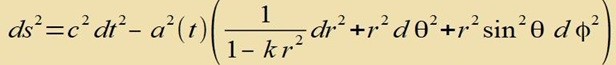 | mit den neuen Bezeichnungen x0=ct, x1=r, x2=Θ und x3=φ. |
| Aus den Linienelement liest man ab und weil giigii=1 sein muss, folgt | 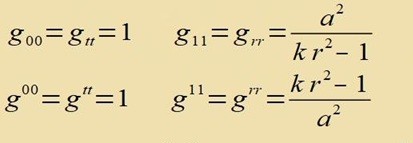 | 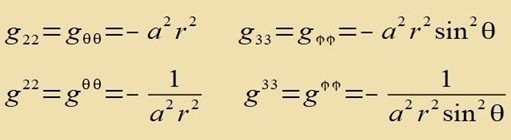
|
| Die Christoffelsymbole | 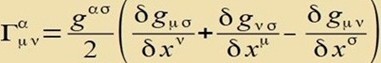 | zu dieser Metrik sind |
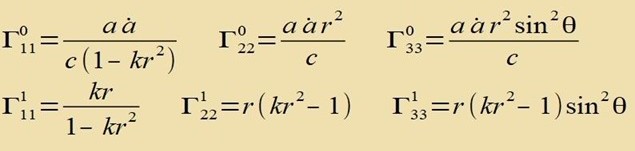 | 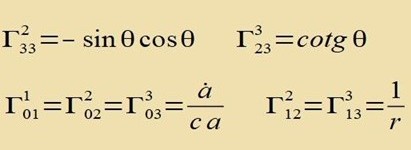 | Alle weiteren Christoffelsymbole sind gleich 0. |
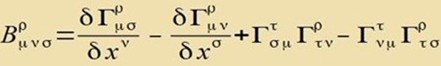 | Der Riemannsche Krümmungstensor wird verjüngt zum Riccitensor | 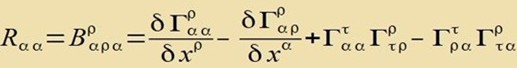
|
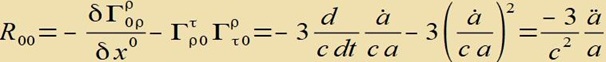
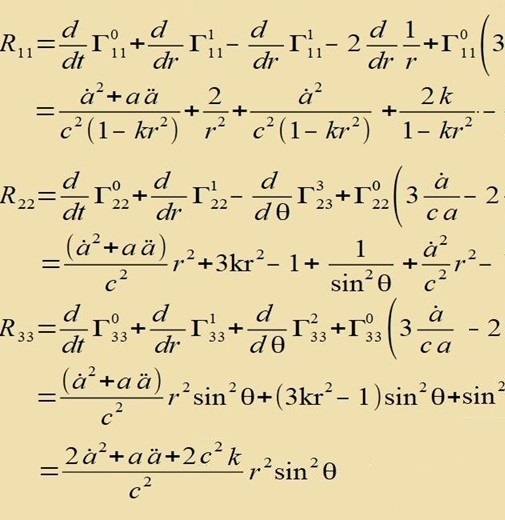 | 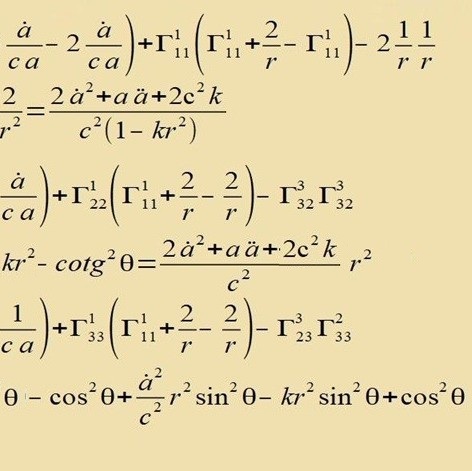
|
| Die Komponenten des Riccitensors sind | 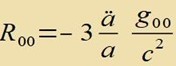 | und mit j=1,2,3 | 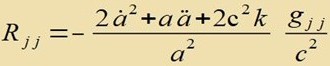
|
| Zu diesem Riccitensor gehört der Ricciskalar | 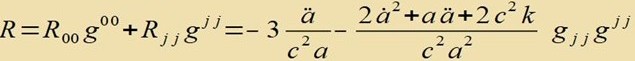 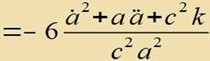
|
Die Komponenten des Einsteintensors sind | 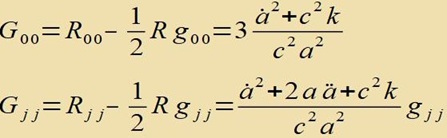
|
Im Ansatz für dl2 gibt es keinerlei Vorzugsrichtung oder Inhomogenität, der Raum ist isotrop und homogen. Das Gleiche wird für die großräumige Dichteverteilung von Materie und Energie angenommen, demnach sind die Galaxien im Universum isotrop und homogen wie Staub oder wie ein ideales Gas verteilt.
| Der Energie-Impuls-Tensor eines idealen Gases (oder einer Flüssigkeit) ist in der Minkowski Raumzeit gegeben durch
ρ: Massen/Energiedichte p: isostatischer Druck u: Vierergeschwindigkeit ηαα=+1 (kontravariante Form!) Es ist u0=(c,0,0,0) und damit u0u0=c2, alle anderen Geschwindigkeiten sind gleich Null | 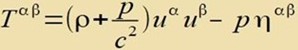
|
| Im Minkowski-Raum |  | In der RW-Metrik | 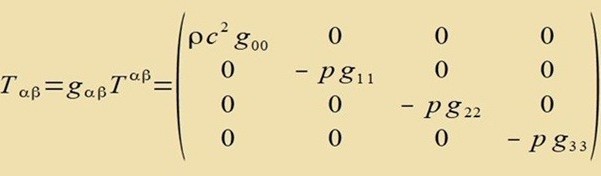
|
| Nun ist alles vorbereitet, um die Feldgleichungen | 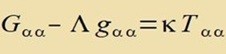 | mit | 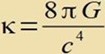 | anzuwenden. |
| Aus | 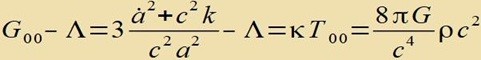 | folgt die erste Friedmann Gleichung | 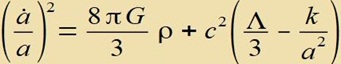
|
| ======================================== | |||
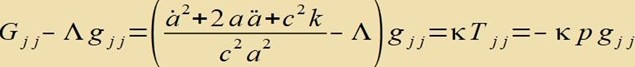 | führt zu | 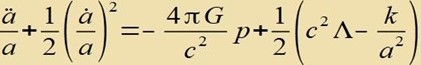
|
| Indem man in dieses Zwischenergebnis die erste Friedmann Gleichung einsetzt, erhält man die zweite Friedmann Gleichung | 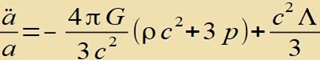
|
| ====================================== |
A