FLRW-Metrik unt Friedmann-Gleixungen |
| Inn der dreidimenzionalen Hüperebene | 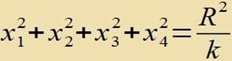 | des ℝ4 vird das Element | 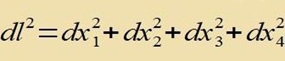 | umgecriben inn r, φ,θ |
| mit den Koordinatentransformatsionen | 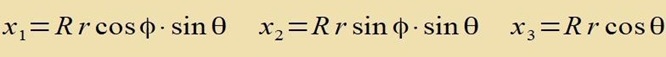
| Man erhält tsunäxst für di dxi |
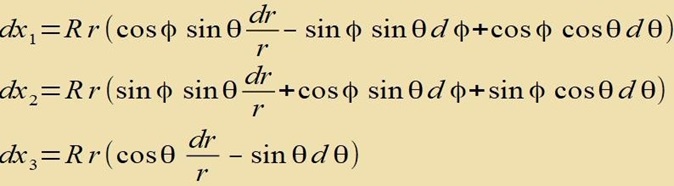 | Venn di Kvadrate der dxi addirt verden, heben zix alle gemiccten Glider dr⋅dφ, dφ⋅dθ unt dθ⋅dr gegenzeitig auf. Es bleibt 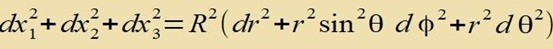
|
| Mit | 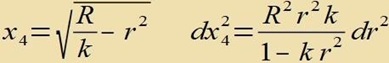 | folgt clislix | 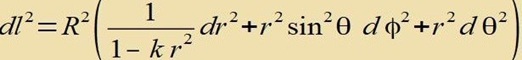
|
| Das Linienelement vird nun gebildet aus tseitlixxem unt räumlixxem Anteil | 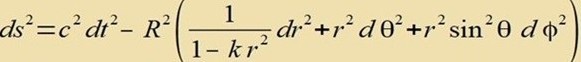
|
Der Parameter R, der für di räumlixxe Gröse des Univerzums cteht, ist vegen dessen Ekspanzion nixt konstant unt muss als tseitlixxe Funktsion a(t) eingezetst verden.
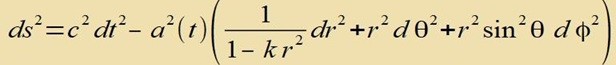 | mit den neuen Betseixnungen x0=ct, x1=r, x2=Θ und x3=φ. |
| Aus dem Linienelement lizt man ap unt veil giigii=1 zein muss, folgt | 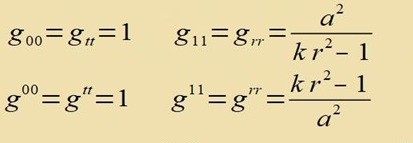 | 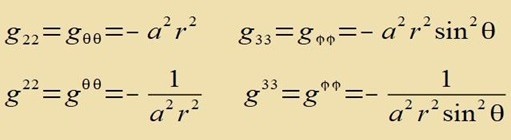
|
| Di Christoffelzümbole | 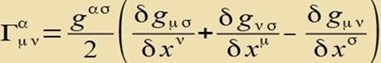 | tsu dizer Metrik zint |
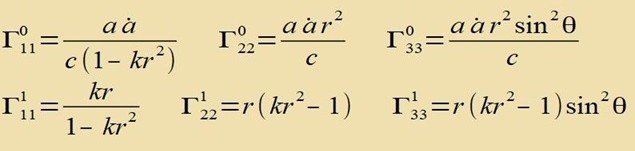 | 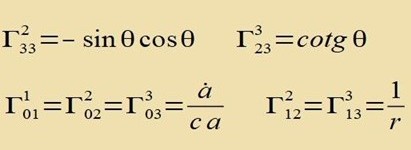 | Alle veiteren Christoffelzümbole zint gleix 0. |
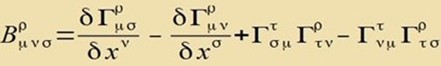 | Der Riemannce Krümmungstensor vird ferjüngt tsum Riccitenzor | 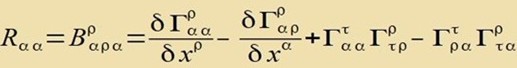
|
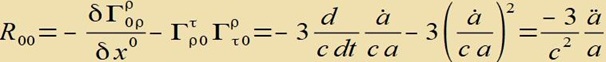
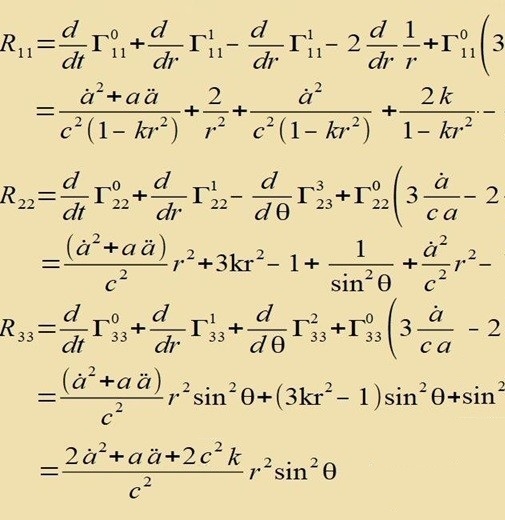 | 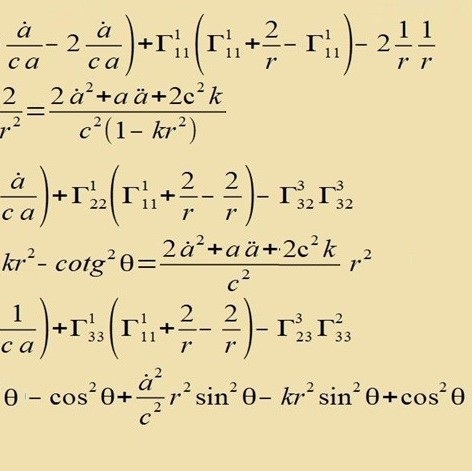
|
| Di Komponenten des Riccitenzors zint | 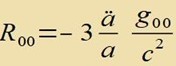 | unt mit j=1,2,3 | 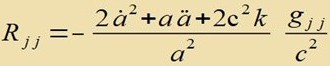
|
| Tsu dizem Riccitenzor gehört der Ricciskalar | 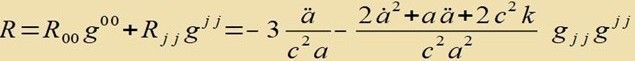 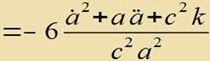
|
Di Komponenten des Einsteintenzors zint | 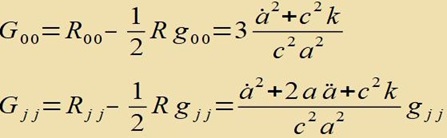
|
Imm Anzats für dl2 gibt es keinerlei Fortsugsrixtung oder Inhomogenität, der Raum ist izotrop unt homogen. Das Gleixe vird für di grosräumige Dixteferteilung fon Materie unt Energi angenommen, demnax zint di Galaksien imm Univerzum izotrop unt homogen vi Ctaub oder vi ein ideales Gaz ferteilt.
| Der Energi-Impulz-Tenzor eines idealen Gazes (oder einer Flüssigkeit) ist inn der Minkowski Raumtseit gegeben durx
ρ: Massen/Energidixte p: izoctaticer Drukk u: Firergecvindigkeit ηαα=+1 (kontravariante Form!) Es ist u0=(c,0,0,0) unt damit u0u0=c2, alle anderen Gecvindigkeiten zint gleix Null | 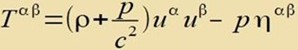
|
| Imm Minkowski-Raum | 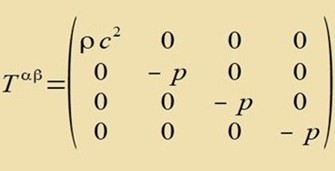 | Inn der RW-Metrik | 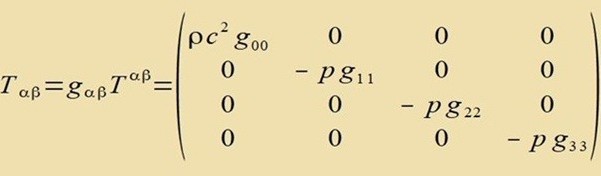
|
| Nun ist alles forbereitet, um di Feldgleixungen | 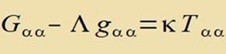 | mit | 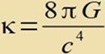 | antsuvenden. |
| Aus | 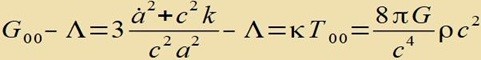 | folgt di erste Friedmann Gleixung | 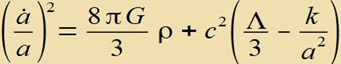
|
| ======================================== | |||
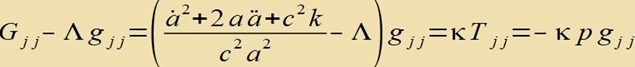 | fürt tsu | 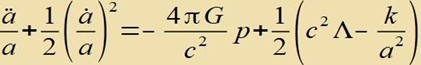
|
| Indem man in dizes Tsviccenergebnis di erste Friedmann Gleixung einzetst, erhält man di tsveite Friedmann Gleixung | 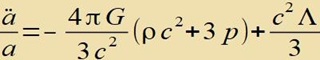
|
| ====================================== |
A