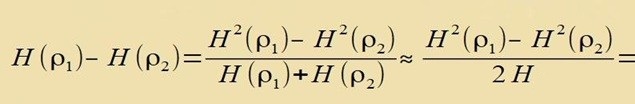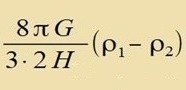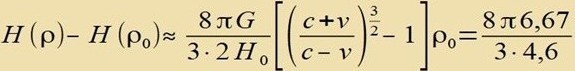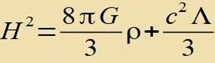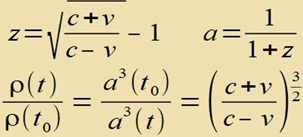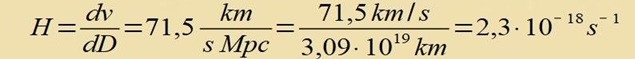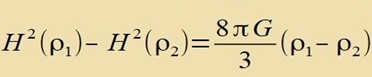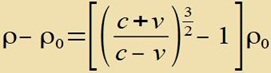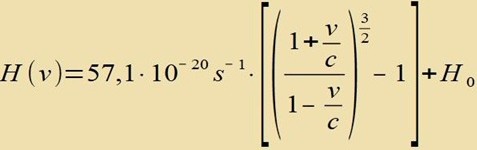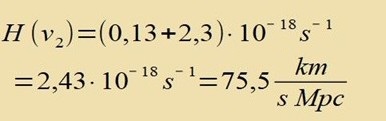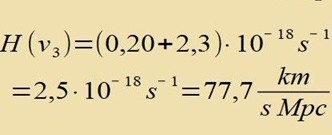Tsurük tsu Kapitel Urknall

Hubble-Parameter unt erste Friedmann Gleixung (inn Arbeit)

	Di erste Friedmann Gleichung (31b) imm Kapitel Urknall ist Imm Hubble Diagramm ist H di Cteigung der Geraden.	(1)
	Auf der Ordinate eines Hubble Diagramms kann valveize di Retsessionsgecvindigkeit v einer Galaksi, inn der di Zupernova eksplodirt ist, oder di Rotfercibung z, oder der Sklalenfaktor a(t) oder clislix di damalige Dixte ρ(t) des Univerzums aufgetragen verden. 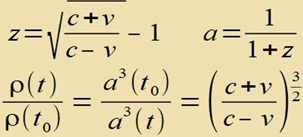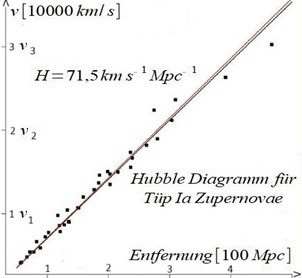Für di Umrexnungren gilt: Das Intervall für v ist 0 ≤ v ≤ 33000km/s Dem entcprexxen di Intervalle 0 ≤ z ≤ 0,117 1 ≤ a ≤ 0,895 ρ(t0) ≤ ρ ≤ 1,39 ρ(t0)	(2) (3)	Functelle Hubble Diagramm
	Die Steigung der Geraden ist die Hubble Konstante 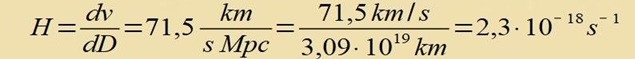Gleixung (1) fürt tsu 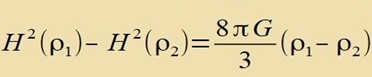Veil inn guter Näherung gilt H(ρ1)+H(ρ2)≈2H0, folgt,	(4) (5) (6)
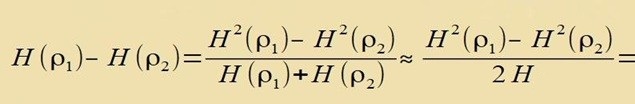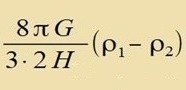
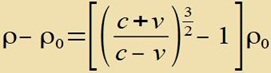
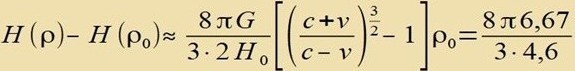
	Di Gleixungen (2) unt (3) ergeben einen Tsuzammenhang tsviccen der Rotfercibung unt der Dixte des Univerzums tsu der Tseit, als das Lixt der Zupüernova ausgezendet vurde. Ist ρ0 di heutige Dixte, dan gilt Di Dixte ρ0 der Masse imm Univerzum vird heute auf 4,7⋅10-27kg/m3 gecätst. Mit Gleixung (6) erhält man Veil ρ eindeutig durx v bectimmt ist, kann H(ρ) als H(v) gecriben verden unt H(ρ0) ist H0. 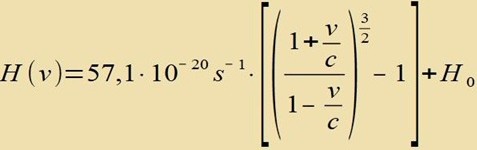Di ekkige Klammer ist eine Funktsion f(v/c). Mit vi=i⋅10000km/s ist f(v1/c)=f(1/30)=0,105, f(v2/c)=f(2/30)=0,221 unt f(v3/c)=f(3/30)=0,349. Es folgt Da di Beobaxtungen näherungsveize auf einer Geraden durch den Urcprung ligen, kann H=dv/dD durx H=v/D erzetst verden. Dan ist D=D(v)=v/H(v) unt es entcteht eine Kurve v(D) (gelbe Kurve), die deutlich fon der Hubble-Geraden (blau) apveixt. Gleixung (1) fürt tsu einem Ergebnis, das imm Vidercpruxx tsu den Beobaxtungen imm Hubble Diagramm cteht.

A