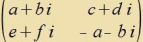Generatoren einer Lie-Algebra

V zei ein n-dimenzionaler Vektorraum über den kompleksen Tsalen. Dan bilden di linearen Transformatsionen, di V bijektiv auf V apbilden, eine Gruppe; denn dize Apbildungen zint assotsiativ, es gibt das neutrale Element unt tsu jeder linearen Transformatsion gibt es di umgekehrte Transformatsion. Mit Ausname des Kommutativgezetses gelten alzo di gleixen Gezetse (Aksiome) vi bei den Tsalen, zodas di cpetsiellen Kommutatsionsregeln eine bezondere Rolle cpilen. Di Gruppe der allgemeinen linearen Transformatsionen vird mit GL(n,ℂ) betseixnet. Di Transfomatsionen aus GL(n,ℂ) verden als Matritsen gecriben, di Elemente fon V als Cpaltenvektoren unt di Transformatsion ist das Matriksprodukt fon Matriks unt Cpaltenvektor, bei dem nur eine Cpalte, alzo vider ein Cpaltenvektor entcteht. Di cpetsielle lineare Gruppe SL(n,ℂ) becteht aus den Matritsen A∈GL(n,ℂ), deren Determinante gleix 1 ist. SL(n,ℂ) ist eine Untergruppe fon GL(n,ℂ). Erzetst man ℂ durx ℝ, zo erhält man di Gruppen der reellen linearen Transformatsionen.

Di Transformirte AT einer Matriks A erhält man, venn man alle Matrikselemente fon A an der Hauptdiagonalen spigelt, zodas alzo di aik durx di aki erzetst zint. Verden auserdem inn der Transformirten alle Matrikselemente durx ire konjugirt kompleksen erzetst, erhält man di Adjungirte A†.

Di Matritsen A∈SL(n,ℂ), für di gilt A†A=E,  bilden eine Untergruppe fon SL(n,ℂ), di unitäre Gruppe SU(n)   unt  di Matritsen A∈SL(n,ℝ), für di gilt ATA=E, bilden eine Untergruppe fon SL(n,ℝ), di ortogonale Gruppe SO(n).

GL(n,ℂ) ⊃ SL(n,ℂ) ⊃ SU(n) ∪ ∪ ∪ GL(n,ℝ) ⊃ SL(n,ℝ) ⊃ SO(n)

Di Matrikseinträge der A∈GL(n) zint Funktsionen, zodas GL(n) unt ire Untergruppen nicht endlixxe Gruppen darctellen. Es zint Lie-Gruppen, topologice Mannigfaltigkeiten, auf denen differentsirt unt integriert verden kann. SO(2) ist di Gruppe der Drehungen um einen Punkt inn der Ebene, SO(3) di Gruppe der Drehungen um einen Punkt imm dreidimenzionalen Raum unt di einfaxxen Lorentztransformatsionen (Lorentz-boosts) verden durx eine Untergruppe der SL(2) becriben. Um einen allgemeinen Überblick über di möglixxen Lie-Gruppen tsu bekommen, unterzuxt man insbezondere di Lie-Algebren: das zint di "Tangentsialräume" an di Lie-Guppen an der Ctelle des neutralen Elementes. Di tsu einer Lie-Gruppe GL(n,ℝ) oder GL(n,ℂ) gehörende Lie-Algebra 𝔤𝔩(n,ℝ) oder 𝔤𝔩(n,ℂ) ist ein Vektorraum über den reellen Tsalen. Di Matritsen A'(E) ctellen di Bazisvektoren der jeveiligen Lie-Algebra dar. Inn den Fertaucungsregeln - den Kommutatoren [A,B]=AB-BA - dizer Bazismatritsen (ctat Bazisvektoren) der Lie-Algebra ist di Ctruktur der Lie-Gruppe festgelegt, zi zint di Generatoren der Lie-Gruppe.

Di Einträge a_ik(t) einer Matriks A(t)∈SL(n) können zo gevält verden, dass a_ik(0)=δ_ik ist (δ_ii=1 unt δ_ik=0 für i≠k). Dan ist A(0) gleix der Einheitsmatriks E, dem neutralen Element der Matriksgruppe. Veil di Determinante einer Matriks A(t)∈SL(n) unaphengig fom Parameter t immer gleix 1 ist, fercvindet di Apleitung der Determinante für jedes t. 

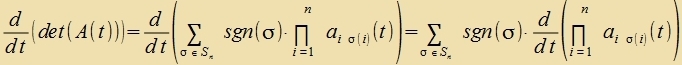	Sn ist di Gruppe der Permutatsionen fon n Elementen, σ(i) di i.te Permutatsion der Tsalen fon 1 bis n unt sgn(σ)=±1, je naxdem, op di Permutatsion gerade oder ungerade ist.	(3)
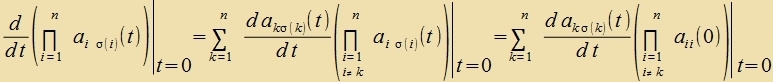	Denn di ak σ(k)(0) zint nur dan fon Null ferciden, venn zi inn der Hauptdiagonalen ctehen. Dan ist das Produkt der n-1 Diagonalelemente gleix 1 unt das differentsirte Matrikselement gehört ebenfalls inn di Hauptdiagonale.	(4)
Zetst man (4) ein inn (3), dan bleibt fon der Summe nur der Summand für di neutrale Permutatsion übrig.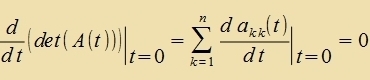

Di Cpur der Apleitung A'(t) einer Matriks A(t)∈SL(n) an der Ctelle t=0 ist alzo gleix der Apleitung irer Determinante unt damit gleix Null. Dize cpurlozen Matritsen A'(0) zint di Bazismatritsen der Lie-Algebra 𝔰𝔩(n,ℝ) oder 𝔰𝔩(n,ℂ), di als Vektorraum über den reellen Tsalen gebildet vird, unt di Generatoren der Gruppe SL(n,ℝ) oder SL(n,ℂ). Vi inn jeder Algebra oder jedem Vektorraum gibt es aux andere Zätse fon Baziselementen, di aber immer untereinander durx Linearkombinatsionen austaucbar zint.

Für A(t)∈SU(n) gilt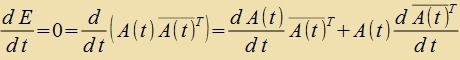

unt vegen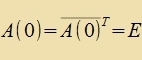

folgt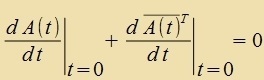

Di Bazismatritsen der Algebra 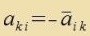𝔰𝔲(n) zint cifhermitece Matritsen

Di Bazismatritsen der Algebra 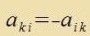𝔰𝔬(n) zint cifzümmetrice Matritsen

(7)

Inn einer cifzümmetricen nXn-Matriks ctehen inn der Hauptdiagonalen nur Nullen unt oberhalb dizer Diagonalen n(n-1)/2 reelle Tsalen. In einer cifhermitecen nXn-Matriks ctehen vegen der tsuzätslixxen Imaginärteile oberhalb der Hauptdiagonalen doppelt zo file reelle Tsalen; datsu kommen n-1 rein imaginäre Tsalen inn der Diagonalen, venn di Cpur fercvindet. Dize frei välbaren reellen Tsalen füren tsu n(n-1)/2 linear unaphengigen Bazismatrtisen der Algebra 𝔰𝔬(n) unt tsu n²-1 linear unaphengigen Bazismatritsen der Algebra 𝔰𝔲(n).

Veiter fordert di Matematik der Lie-Algebren di Gültigkeit der Jacobi-Identität für je drei Bazismatritsen: [A,[B,C]]+[B,[C,A]]+[C,[A,B]]=0

Analog tsur Funktsionenteori vird für jede kvadratice Matrik X das Matrikseksponentsial exp(X) durx di Eksponentsialreihe definirt. Für exp(X) gilt di Gleixung e^Xe^Y=e^X+Y imm allgemeinen nixt; denn aus XY≠YX folgt e^Xe^Y≠e^Ye^y, veil bei der Multiplikatsion der Reihen di Reihenfolge der Matritsen nixt geändert vird, aber e^X+Y=e^Y+X  zein muss. Dize Funktsionalgleixung gilt für fertaucbare Matritsen X, Y unt mit t∈ℝ unt einer Matriks B gilt exp(t₁B)∙exp(t₂B)=exp((t₁+t₂)B)=exp(t₂B)∙exp(t₁B). Di Matritsen A(t)=exp(t∙B) bilden eine abelce Lie-Gruppe mit exp(-t∙B)=A^-1(t) unt A(0)=A⁰=E. Di Apleitung fon A(t) nax t ist B∙A(t) unt an der Ctelle des neutralen Elementes gleix B. Di Matriks B, mit der di Gruppe konstruirt vurde, ist alzo ein Generator der abelcen Lie-Gruppe A(t).


Untergruppen fon SL(2,ℂ)

Fon den fir reellen Tsalen xjk einer cpurlozen reellen 2x2-Matriks zint drei frei välbar. Deshalb zint höxstens drei Matritsen linear unaphengig, di Lie-Algebra 𝔰𝔩(2,ℝ) ist ein dreidimenzionaler Vektorraum.

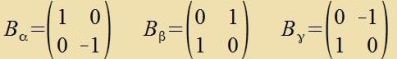(8)

Für dize Bazismatritsen der Lie-Algebra 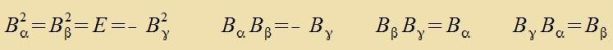𝔰𝔩(2,ℝ) gilt
Di Fertaucungsrelatsionen der Matritsen zint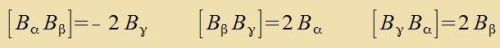

Alzo gilt entveder oder es ist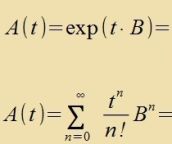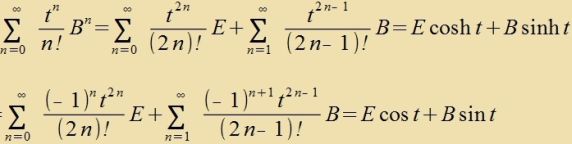

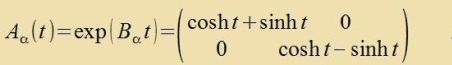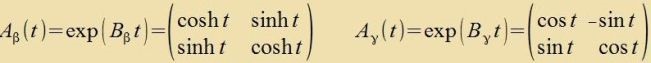	(13)
Dis zint drei einparametrige abelce Untergruppen fon SL(2,ℝ)⊂SL(2,ℂ). Nur Aγ(t) ist ortogonal, veil nur Bγ cifzümmetric ist.

Di Bazismatritsen der Lie-Algebra 𝔰𝔲(2) zint komplekse antihermitece 2x2-Matritsen. In der Hauptdiagonalen können daher nur rein imaginäre Tsalen ctehen.

Bedingungen für dize Matritsen zint: x1,1=-x2,2 unt aus x2,1=a+bi folgt x1,2=a-bi. Es bleiben drei Freiheitsgrade, di Lie-Algebra ist dreidimenzional.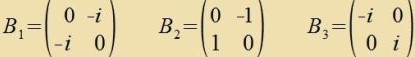

B1, B2, B3 erfüllen di Bedingungen.

(14)

Aus		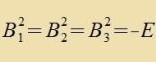folgt		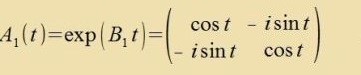	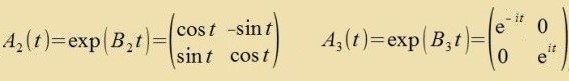(15)
Dis zint drei einparametrige abelce Untergruppen fon SU(2)⊂SL(2,ℂ). Di Gruppe Aγ(t)=A2(t) ist als Untergruppe zovol inn SU(2) als aux inn SL(2,ℝ) enthalten.

Di Produkte der Matritsen (14) zint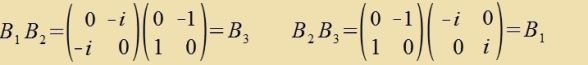

unt vegen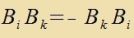

folgt für di Bazismatritsen der 𝔰𝔲(2)

(17)

Drei fercidene Buxctaben inn alfabeticer Reihenfolge als Inditses zollen immer für di Indeksfolgen 1,2,3 oder 2,3,1 oder 3,1,2 ctehen.

Inn dizer tsüklicen Creibveize gilt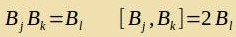

Di Lie-Algebra 𝔰𝔲(2) ist mit dizen drei Bazismatritsen inn zix geclossen.

(18)

Di reelle Lie-Algebra 𝔰𝔲(2) kann mit den Kommutatoren eineindeutig auf den dreidimenzionalen euklidischen Raum apgebildet verden, vobei di Kommutatoren dem Vektorprodukt entsprexxen. Zo zint dize beiden Strukturen tsu einander izomorf unt inn beiden gilt [B₁,[B₂,B₃]]+[B₂,[B₃,B₁]+[B₃,[B₁,B₂]]=0 unt entcprexxend r₁⨯(r₂⨯r₃)+r₂⨯(r₃⨯r₁)+ r₃⨯(r₁⨯r₂)=0. Dize Betsihung, di imm Dreidimenzionalen fast trivial erceint, gilt bei der Konstruktsion fon Lie-Algebren höherer Dimenzion als Aksiom (Jacobi-Identität).

Um jedes Element der Form inn der reellen Algebra 𝔰𝔩(2,ℂ) dartsuctellen, brauxt man 6 linear unaphengige Bazismatritsen. Fon den 6 Matritsen (8) unt (14) zint 5 linear unaphengig. Eine 6. cpurloze Matriks, di als linear unaphängiger Bazismatriks inn 𝔰𝔩(2,ℂ) hinzukommt, ist

Bildet man mit allen Matritsen B di Algebra über den kompleksen Tsalen, zo erhält man di kompleksifitsirte Lie-Algebra 𝔰𝔩(2,ℂ)_ℂ. Vegen iB₁=B_β, iB₂=B₀ unt iB₃=B_α genügen di drei Bazismatritsen der 𝔰𝔲(2) als Baziszüstem der 𝔰𝔩(2,ℂ)_ℂ. Dize komplekse Lie-Algebra hat tsvei reelle Formen, di cpaltbare 𝔰𝔩(2,ℝ) unt di kompakte 𝔰𝔲(2) mit den tsugehörigen Lie-Gruppen SL(2,ℝ) - Gl. 13 - unt unt SU(2) - Gl. (15) -. Dize ausfürlixxe rexnerice Darctellung der Lie-Gruppe SL(2,ℝ) mag als Ferancaulixxung allgemeiner Zätse aus der Matematik der Lie-Algebren dinen.

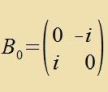
SL(2,ℂ) hat zeks einparametrige abelce Untergruppen. Di Determinanten aller 6 Matritsen haben den Vert +1.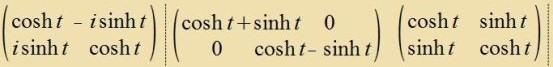

(20)

SO(3) unt SU(3)

Für n=3 gibt es drei linear unaphengige cifzümmetrice Matritsen (xkk=0 unt x1,2=-x2,1≠0 oder x2,3=-x3,2≠0 oder x3,1=-x1,3≠0)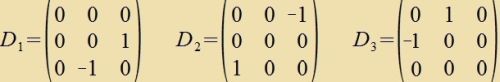

mit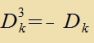

(21)

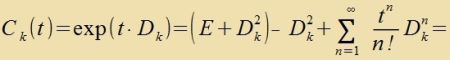
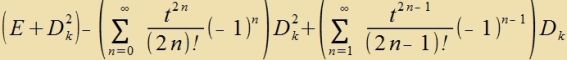
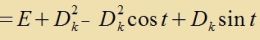Das zint di drei abelcen Untergruppen der SO(3), der Drehungen um drei tsu einander zenkrexte Aksen imm Raum.

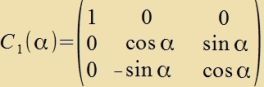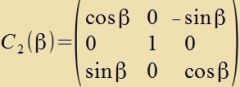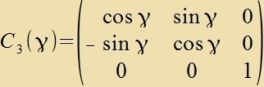(23)

Di D_k bilden ein Baziszüstem der Lie-Algebra 𝔰𝔬(3), di Lie-Gruppe SO(3) becteht aus den drei Untergruppen C_k(t).

Di Dimenzion der Lie-Algebra 𝔰𝔲(3) ist n²-1=8. Eine axtdimenzionale Bazis unt di Kommutatoren dizer cifhermitecen Bazismatritsen zint:

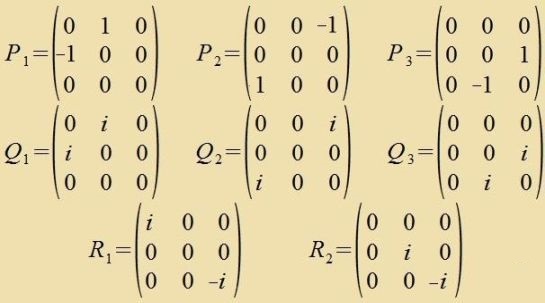(24)

Di Bazismatritsen D_i der 𝔰𝔬(3) zint gleixtseitig drei der axt Bazismatritsen der 𝔰𝔲(3), veil SO(3) eine Untergruppe der SU(3) ist. Mit Ausname fon [P₂,Q₂]=2(R₁+R₂), das inn der Tabelle tsur Apkürtsung als 2R₃ erceint, ergeben alle Kommutatoren vider eine Bazismatriks. Tsum Naxveiz der Jacobi Identität vird eine Funktsion f(A,B,C) definirt.

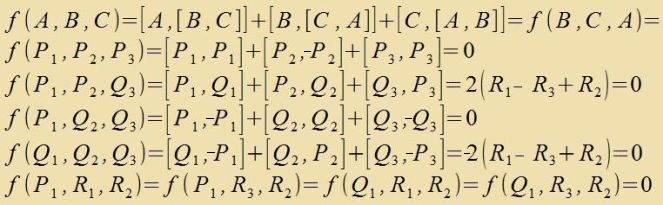Di Matritsen Pi, Qi, R1 unt R2 erfüllen di Jacobi Identität, zi bilden eine Bazis der Lie-Algebra 𝔰𝔲(3) unt zint di Generatoren der Lie-Gruppe SU(3).

(25)

Di eigentlix ortoxrone Lorentz-Gruppe inn SL(4,ℝ)

Di Matritsen der Lorentz-Transformatsionen zint reell unt haben di Determinante 1, zint aber nixt ortogonal. Deshalb vird di Lorentz-Gruppe inn den Untergruppen fon SL(4,ℝ) gezuxt. Veil alle Einträge der Bazis-Matritsen fon 𝔰𝔩(4,ℝ) reel zint, gibt es 4(4-1)/2=6 Bazis-Matritsen. Drei 4X4-Matritsen G_i entctehen, venn inn den drei Matritsen D_k aus (21) oben je eine Tseile unt links je eine Spalte mit Nullen hintsufügt vird. Di übrigen drei Matritsen F_i enthalten außer 0 nur inn den tsugefügten Tseilen und Cpalten je eine 1.

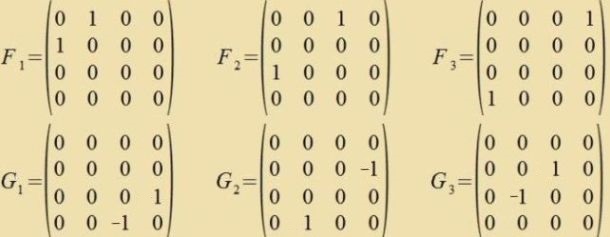Es gilt Fi3=Fi unt Gi3=-Gi. Mit dem Matrikseksponentsial erhält man di Untergruppen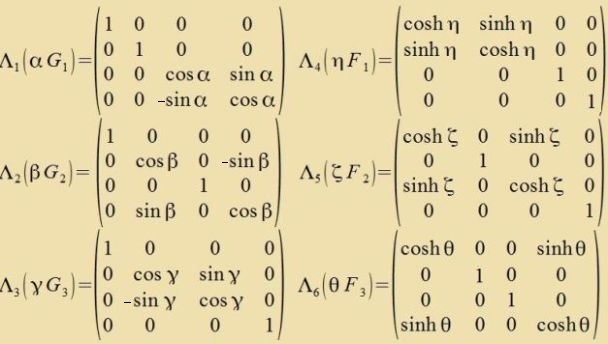

Di Kommutatoren zint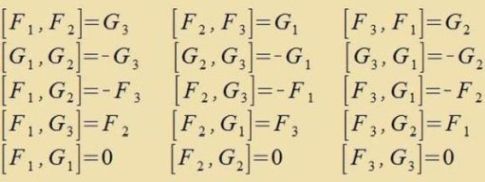 f(A,B,C) zei vider di in (25) definirte Funktsion. 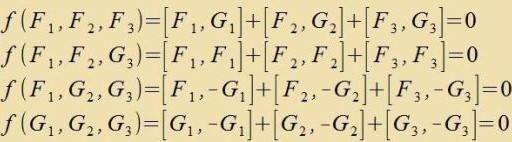Damit ist di Bedingung der Jacobi Identität erfüllt. Für cpäter: [Fi,Fj]+[Gi,Gj]=0 unt [Fi,Gj]-[Gi,Fj]=0 Das Matrikseksponentsial ertseugt aus den zeks Bazismatritsen zeks einparametrigen abelcen Untergruppen fon SL(4,ℝ) Veil drei Untergruppen fon SL(4,ℝ) eine räumlixxe Drehgruppe enthalten, vird di Gruppe aux mit SO(1,3) betseixnet.

(27) (28)

Zetst man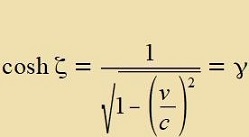

dan gilt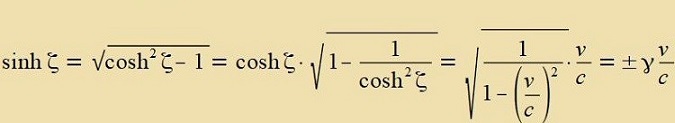

(29)

Di Transformatsion Λ₄ ist gleich dem Lorentz-Boost (4) inn Kapitel XXIII. Raum-Tseit. Jedes Λ_i ist entveder ein Lorentz-Boost oder eine räumlixxe Drehung, SL(4,ℝ) oder O(1,3) ist damit di Lorentz-Gruppe. Für di Anvendung als Koordinatentransformatsion inn der Füzik müssen Cpigelungen unt eine falce Tseitrixtung ausgeclossen verden, das vird durx ein hoxgectelltes Plustseixen markirt. SO⁺(1,3) ist di Gruppe der eigentlixxen ortoxronen Lorentz-Transfomatsionen, man schreibt L^†₊=SO⁺(1,3).

Di 6 Matritsen F_i unt G_i zint di Bazis-Matritsen der Lie-Algebra 𝔰𝔩(4,ℝ), dis ist di Lorentz-Algebra.



Das direkte Produkt SU(2)XSU(2)

Für di Matritsen Fk unt Gk (Gl. (27)) gilt		(30)
Nun vält man als neue Bazismatritsen		(31)
Für dize Bazismatritsen gilt		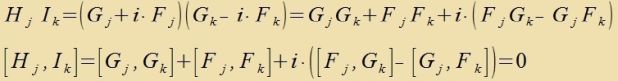(33)

Di H_k fertaucen mit den I_k. Daher tserfällt di Lie-Algebra inn tsvei Unteralgebren.

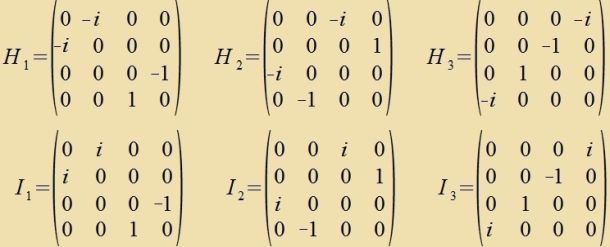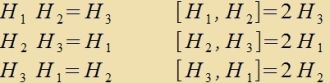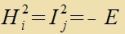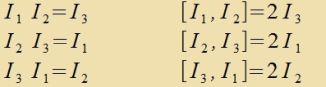
(34) (35) (36)

Di Algebra gebildet mit den Bazismatritsen H_k über den reellen Tsalen unterceidet zix inn nixts fon der Lie-Algebra 𝔰𝔲(2), da di Fertaucungsregeln der H_k mit denen der Bazismatritsen B_k fon 𝔰𝔲(2) übereictimmen (fergleixe (34) unt (17)). Dize beiden Algebren zint izomorf. Da aux di Fertaucungsregeln der I_k mit denen der B_k übereinctimmen, ist aux di Algebra, di mit den Bazismatritsen I_k über den reellen Tsalen gebildet vird, izomorf tsu 𝔰𝔲(2). Di Lorentz-Algebra 𝔰𝔩(4,ℝ) ist gleix der der Algebra, di aus tsvei 𝔰𝔲(2) gebildet vird: 𝔰𝔩(4,ℝ) = 𝔰𝔲(2) x 𝔰𝔲(2). Daraus folgt

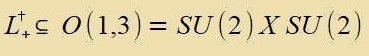(37)

Für einen 'boost' mit Drehung um di Relativgecvindigkeit ist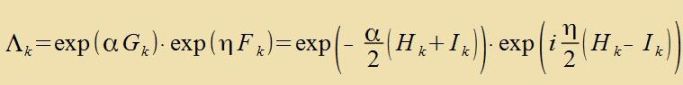
Vegen [HK,Ik]=0 (33) können di Argumente addirt verden		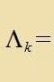	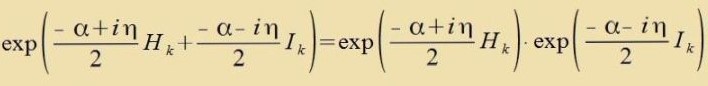(39)

Veil di H_k unt di I_k dizelbe Fertaucungsregeln befolgen unt dize gleix den Fertaucungsregeln inn Gleiung (17) zint, ist mit Gleixung (39) di Tserlegung der eigentlix ortoxronen Lorentzgruppe inn tsvei Reprezentatsionen A_H unt A_I der Gruppe SU(2) entcprexxend Gleixung (37) folltsogen. Di beiden Reprezentatsionen zint nixt änlix, es gibt keine Matriks S für eine Änlixkeitstransformatsion SA_HS^-1=A_I, veil di konjugirt-kompleksen Faktoren α±iη zo nixt inn einander überfürt verden können.

Multiplitsirt man einen antihermitecen oder cifzümmetriceb Generator mit i, erhält man eine hermitece Matriks i∙A. Mit exp(-i∙t∙(iA)) vird dan das urcprünglixxe Matrikseksponentsial viderhergectellt. Zo erhält man aus den Generatoren (17) der SU(2) die Paulimatritsen, di imm Kapitel XXIII. Raum-Tseit definirt zint.

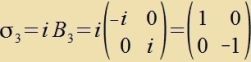	mit tsüklicer Fertaucung der j, k, l	(41)

Ein Bazisveksel inn der Lie-Algebra 𝔰𝔲(2) fon den H_k unt I_k tsu den Pauli-Matritsen unt neue Parameter bringen Gleixung (39) auf di üblixxe Form

Di beiden Faktoren zint tsvei nixt-änlixxe Darctellungen der Lie-Gruppe SL(2,ℂ).

(42)

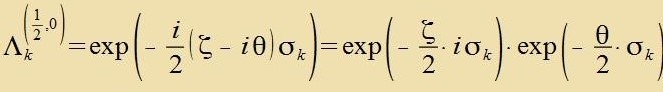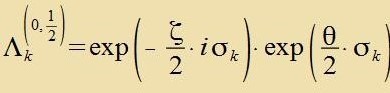(43)

Jede der beiden Darctellungen ist kompakt unt einfaxx tsuzammenhengend unt überdekkt di eigentlix ortoxrone Lorentzgruppe. Tsu jeder der beiden Darctellungen gehören vider zeks einparametrige Untergruppen, di als Transformatsionen imm tsveidimenzionalen Vektorraum über den kompleksen Tsalen virken. Das ist der Raum der (tsveidimenzionalen) Spinoren.

Dirac-Matritsen

Di Elemente des direkten Produktes tsveier Gruppen verden mit dem Kronecker-Produkt berexnet. B₁=A₁(π/2), B₂=A₂(π/2), B₃=A₃(π/2) unt E=A₁(0)=A₂(0)=A₃(0) zint fir Elemente der Gruppe SU(2) (Gleixungen (8) unt (11)). Di Tabelle tseigt di 16 Kronecker-Produkte dizer fir Elemente.

Für i, j, k, l = 1, 2, 3 unt j, k, l tsüklic fertaucend gilt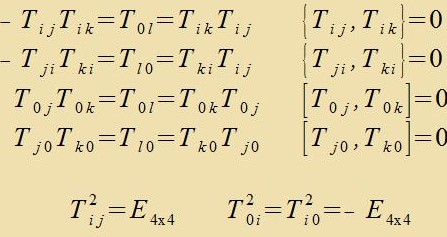

Di T_ij innerhalb der grünen Umrandung zint hermitece Matritsen (A^†=A), di übrigen T_ij zint - auser der Einheitsmatriks T₀₀ - antihermitece Matritsen.

Imm vezentlixxen zint inn der Tabelle di Dirac-Matritsen con enthalten (blau umrandet). Ein Bazisveksel fon den Generatoren B der SU(2) tsu den Pauli-Matritsen ergibt

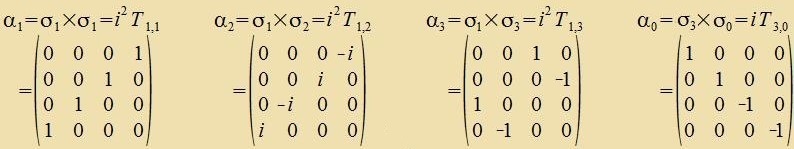Für alle Dirac-Matritsen α gilt (i≠k)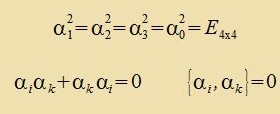

(44)

Da für di Dirac-Gleixung alle Matritsen α antikommutiren müssen, muss α₀ aus einer anderen Tseile genommen verden als di übrigen α.
Das gilt aux für den folgenden tsveiten Zats fon Dirac-Matritsen, der ebenfalls con inn der Tabelle enthalten ist (rot-braun umrandet).

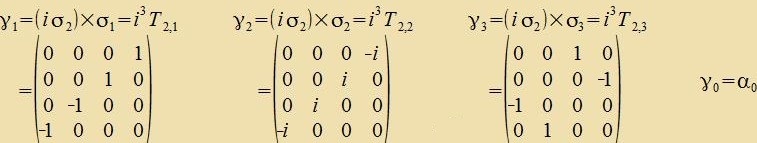Für alle Dirac-Matritsen γ gilt (i≠k)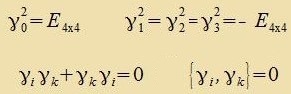

(45)

Man kann di Dirac-Matritsen als Blokkmatritsen creiben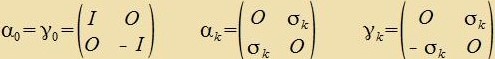
Hir zint O unt I di 2x2-Matritsen		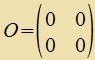unt		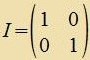	Tsviccen α unt γ gelten di Umrexnungen

Hir geht es tsurük tsu Kapitel XXX. Relativität unt Spin

Darctellung fon Firervektoren durx hermitice 2X2-Matriten

Inn der Raumtseit kann der Firerort (ct,x) aux durx eine hermitece 2X2-Matriks zo dargectellt verden, dass deren Determinante gleix der Firernorm ist.

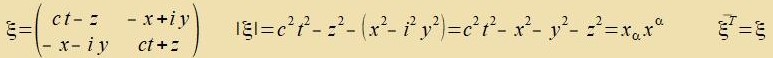(50)

Umgekert kann jeder hermitecen 2X2-Matriks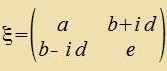

mit reellen a, b, d, e der Firerort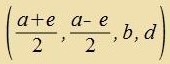

tsugeordnet verden.

(51)

Dan gilt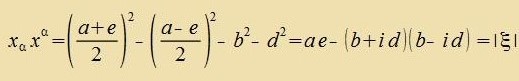

Di Determinante ist vider gleix der Firernorm.

(52)

Di Darctellungen fon Ort unt Tseit eines Ereignisses imm Minkowskiraum durx Firervektoren oder durx hermitece 2x2-Matritsen zint gleixvertig. Di Firernorm eines Firervektors unt di Determinante der entcprexxenden hermitecen 2x2-Matriks ctimmen überein.

Mit den Pauli-Matritsen (einclislix der Einheitsmatriks) vird jeder Firervektor x_α linear inn di tsugehörigen Matriks ξ transformirt.

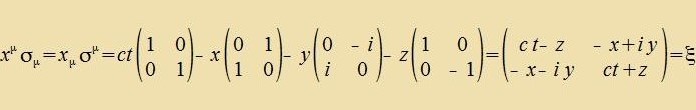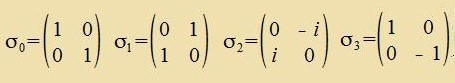(53)

Es gilt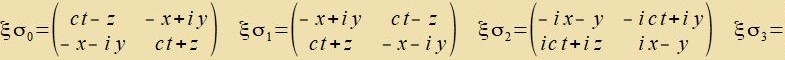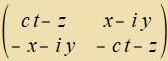

alzo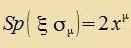

(54)

Vi man ziht, haben di Pauli-Matritsen ire Vurtseln inn der Raum-Tseit der cpetsiellen Relativitätsteori.

Zint ξ unt S tsvei reguläre Matritsen gleixer Dimenzion, dan ist Det(ξ S)=Det(S ξ)=Det(ξ)∙Det(S) unt (ξ S)^T=S^Tξ^T. Venn nun ξ hermitec ist,

dan gilt für de Apbildung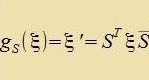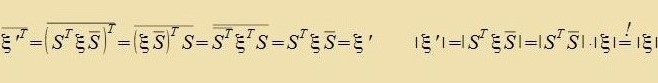

Für jede reguläre Matriks S fürt di Apbildung g_S(ξ) vider tsu einer hermitecen Matriks unt, venn di Determinante fon S gleix eins ist, ctimmen di Determinanten fon ξ unt ξ'=g_S(ξ) überein. Det(S)=1 bedeutet bei 2x2-Matritsen S∈SL(2,ℂ). Parallel tsur Apbildung g_S, di inn der Algebra der hermitecen 2x2-Matritsen ξ auf ξ' apbildet, gibt es dan imm Minkowskiraum der Firenvektoren eine Apbildung Γ_S, di x^μ=½Sp(ξσ_μ) auf x'^μ=½Sp(ξ'σ_μ) apbildet. Γ_S ist eine Lorentztransformatsion unt zo vird eindeutig jedem S∈SL(2,ℂ) ein Element aus einer Teilmenge L fon L^†₊ tsugeordnet. Venn es inn SL(2,ℂ) Elemente gäbe, denen Randelemente fon L tsugeornet vären, dan vären diese keine inneren Elemente fon SL(2,ℂ). Das ist aber nixt möglix, veil SL(2,ℂ) kompakt unt einfaxx tsuzammenhengend ist. Daher gibt es aux tsu jedem Element fon L^†₊ mindestens ein Element inn SL(2,ℂ), dem es tsugeordnet ist. Beide Gruppen verden zurjektiv auf einander apgebildet. Veil aber g_-S(ξ)=g_S(ξ) ist, vird L^†₊ durx SL(2,ℂ) tsveifaxx überdekkt.

Di Matritsen eines Produktes können aux unter der Cpur fertauct verden. Für di Apbildung g_U(ξ) mit einer unitäre Matriks U∈SU(2)⊂SL(2,ℂ) gilt dan tsuzätslix

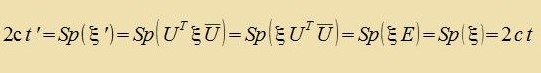
One Änderung der Tseit redutsiren zix Lorentztransformatsionen auf räumlixxe Drehungen. Den Elementen der Gruppe SU(2) verden di Elemente der Gruppe SO(3) tsugeordnet unt vegen g_-U(ξ)=g_U(ξ) vird SO(3) von SU(2) doppelt überdeckt.

Dize Ferflextungen der Transformatsionsmatritsen geben ein Bild fon der inneren Struktur der Raum-Tseit, das allerdings kaum oder tsur menclixxen Forctellung passt.

Hir geht es tsurük tsu Kapitel XXIII. Raumtseit