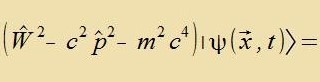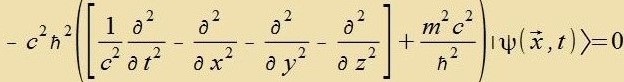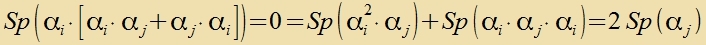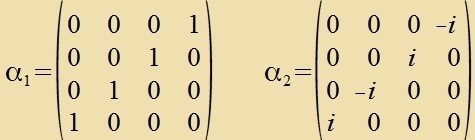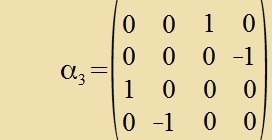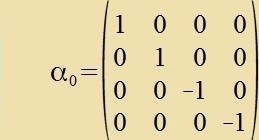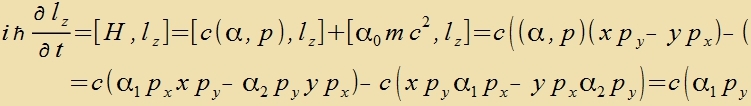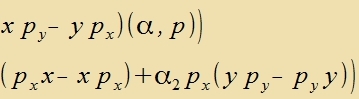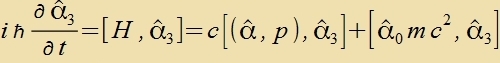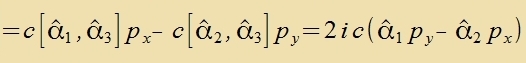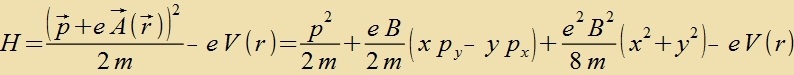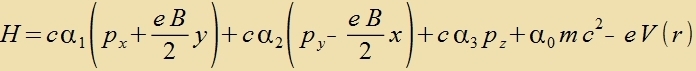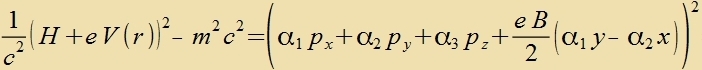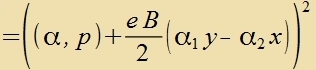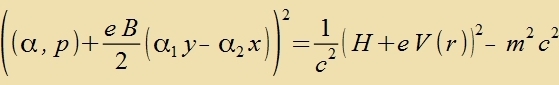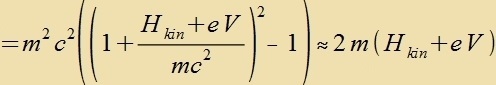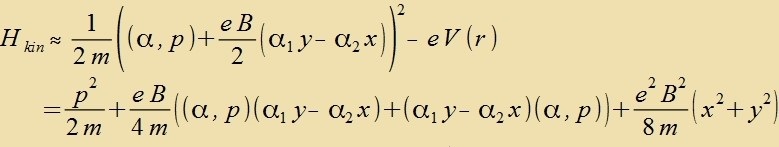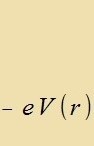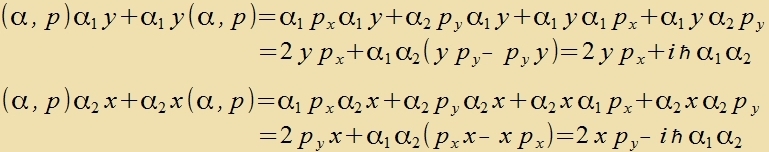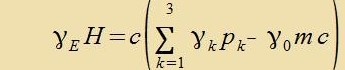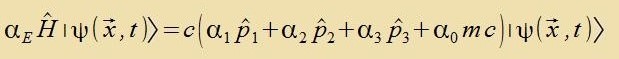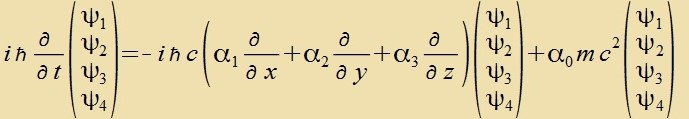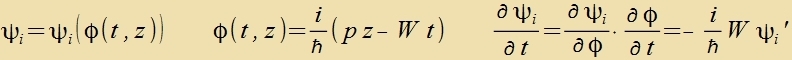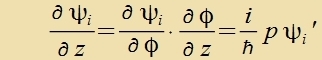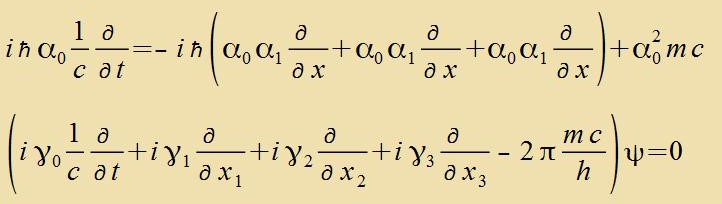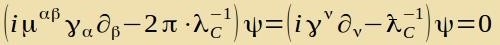Spin

Zer bald nax der Entdekkung der Kvantenmexanik vurde nax Lözungen der Schrödingergleixung gezuxt, di relativistic invariant zint.

Ausgangspunkt ist Einsteins Gleixung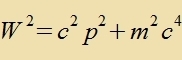

Kapitel XXII, Gleixung (32)

(1)

Mit den Differentsialoperatoren vird daraus
Kapitel XXVII, Gleixung (2)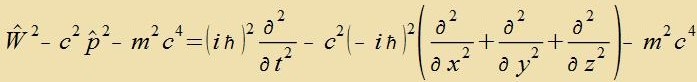

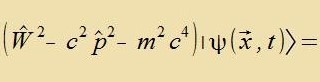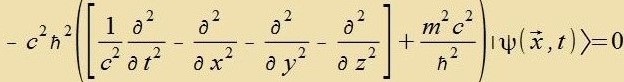
(3)

Mit dem d'Alembert-Operator creibt man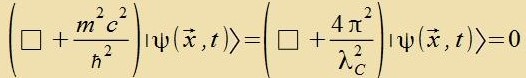

λ_C ist di Compton-Vellenlänge.
Kap. XXV, Gl. (13)

Da c, h unt m konstant zint, gilt für alle Inertsialzüsteme
Kap. XXIII, Gl. (55)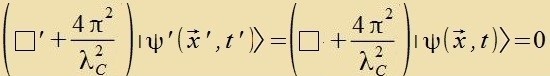

(5)

Dize Klein-Gordon-Gleixung ist eine Vellengleixung für ein skalares Feld. Für m=0 ist zi di Gleixung für eine elektromangnetice Velle. Dan ist das Foton mit fercvindender Ruhemasse ein Teilxen, das di elektromangnetice Vekselvirkung fermittelt. Zo ligt es nahe, Gleixung (5) aux für eine nixt fercvindende Ruhmasse als Vellengleixung eines Feldes mit Austaucteilxen tsu interpretiren. Lözungen zint:

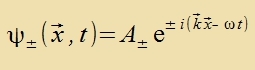mit der Bedingung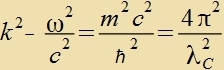

unt umgeformt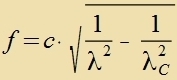

Da für Vellenlängen, di gröser als di Compton-Vellenlänge zint, di Frekvents imaginär vird, ist di Reixveite des Feldes auf di Grösenordnung der Compton-Wellenlänge begrentst. Venn imm d'Alembert-Operator di tseitlixxen Apleitungen gectrixxen, der Laplace-Operator inn Polarkoordinaten gecriben unt clislix di Vinkelapleitungen ebenfalls gectrixxen verden, dan geht di Klein-Gordon-Gleixung über inn eine Gleixung für ein tsentralzümmetrices Potentsial V(r).

(7)

Mit dem Anzats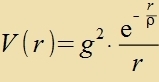

folgt vegen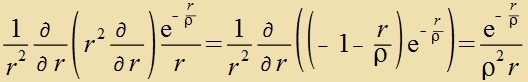

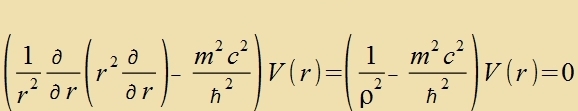Di Lözung ist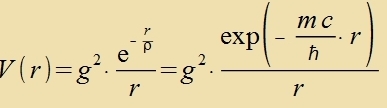

(9)

V(r) ist das Yukawa-Potentsial. Venn ρ als Reixveite der Kernkräfte angesehen vird unt dementcprexxend gleix dem Durxmesser eines Nukleons gezetst vird, erhält man di Grösenordnung der Masse des Austaucteilxens.

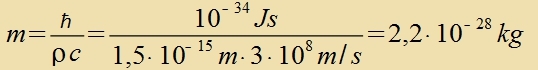Veil dize Masse tsviccen den Massen fon Elektron unt Proton lag, nannte Yukawa das zo fon im forhergezagte Teilxen "Meson". Tatzäxxlix vurde cpäter das nur um rund 50% cverere Pion als Austaucteilxen der ctarken Vekselvirkung identifitsirt.

Erst mit der Kvantenfeldteori vurde di Klein-Gordon-Gleixung veiter bearbeitet; denn ire kvantenmexanice Behandlung fürt tsu negativen Varceinlixkeiten, di Dirac feranlassten, einen neuen Hamiltonoperator für das freie Teilxen mit der Ruhmasse m tsu zuxen. Er 'linearizirte' di Gleixung (1) mit Matriksoperatoren α (α_E zei di Einheitsmatriks der entcprexxenden Dimenzion).

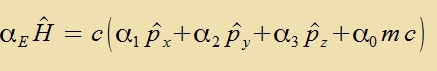mit den Bedingungen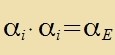

unt für i≠j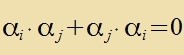

(10)

Vegen der ersten Bedingung können di Eigenverte der α nur +1 oder -1 zein, unt veil allgemein gilt Sp(A∙B)=Sp(B∙A), folgt

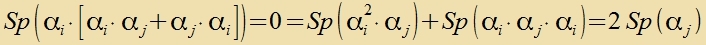
Veil di Cpur einer Matriks gleix der Zumme irer Eigenverte ist, muss di Tsal der pozitiven (+1) gleix der Tsal irer negativen (-1) Eigenverte zein. Di Matritsen α_i haben gerade Dimenzion. Di drei Pauli-Matritsen erfüllen tsvar di Bedingungen, es gibt aber keine firte 2X2-Matriks, di mit inen antikommutirt. Deshalb müssen di Matritsen α_i mindestens di Dimenzion 4 haben. Dirac fand 1928 di Matritsen

(12)

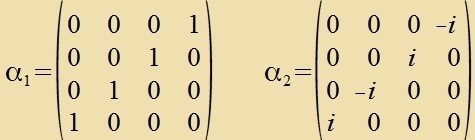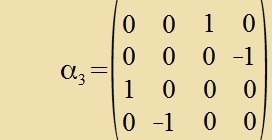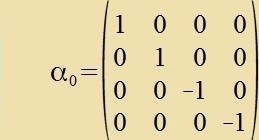
Dize Matritsen (fergleixe Anhang L: Dirac-Matritsen) erfüllen di Bedingungen, zi antikommutiren mit einander unt ir Kvadrat ist die Einheitsmatriks. Zi zint hermitec unt ctellen einen Operator dar für eine Opzervable, di inn der klassicen Füzik unbekannt ist. Damit das Kvadrat des Hamiltonoperators (10) mit Gleixung (1) übereinctimmt, müssen di Impulzoperatoren mit den α-Matritsen fertaucen.

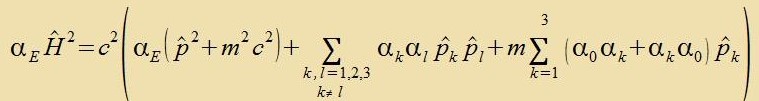mit p₁=p_x, p₂=p_y unt p₃=p_z

(13)

Der letste Zummand fercvindet, veil α₀ mit allen anderen α antikommutirt, der forletste, veil di Impulzoperatoren vertaucen unt di α-Matritsen antikommutiren. Übrig bleibt, venn jetzt di Einheitsmatriks veggelassen vird, Gleixung (1) inn Operatorform.

(14)

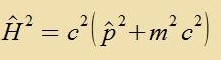
Imm folgenden vird das Operator-Tseixen ^ nur nox gecriben, um den Karakter einer Gröse als Operator tsu betonen. Aux di Einheitsmatriks fällt, venn möglix, fort.

Neben den α-Matritsen gibt es einen tsveiten vixtigen Zats antikommutirender 4x4-Matritsen, di γ-Matritsen. Zovol di α_k als aux di γ_k können als Blokkmatritsen mit den Pauli-Matritsen σ_k dargectellt verden.

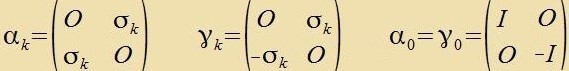mit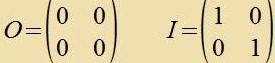

Für di α_k gilt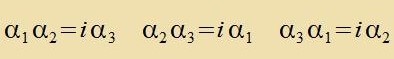

unt genau zo für di γ_k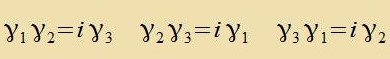

(15)

(16)

Veil mit den Pauli-Matritsen ein Hinveiz auf den Spin gegeben ist, zoll one Festlegung einer Fortsugsrixtung eine Komponente des Drehimpulzes mit dem Hamiltonoperator fon Dirac unterzuxt verden. Di Creibveize (α,p)=α₁p₁+α₂p₂+α₃p₃ zoll der Apkürtsung dinen, es ist kein Skalarprodukt!

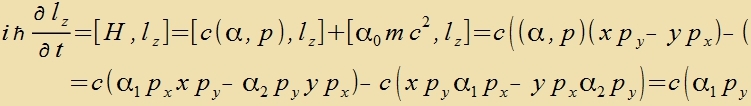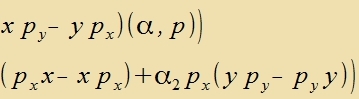
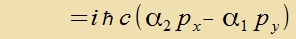ist ungleix Null! Es gibt keine klassic räumlixe Drehimpulzkomponente, di tseitlix konstant väre.

(19)

Di α-Matritsen ctellen einen inneren Freiheitsgrad des Elektrons dar, tsu dem es inn der Ancauung oder der klassicen Füzik nixts Eentcprexxendes gibt. Der Operator, der dizen Freiheitsgrad becreibt, hat keine Bindung an Ort oder Impulz des Elektrons, er ist mit jedem Orts- oder Impulzoperator fertaucbar. Värend di α-Matritsen feste Grösen zint, gilt das nixt für den tsugehörigen Operator, er hat eine Apleitung nax der Tseit.

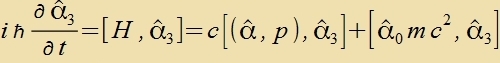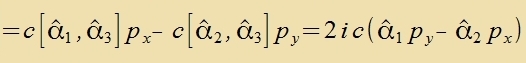
Denn für di Matritsen (13) gilt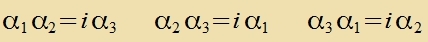

unt daszelbe gilt dan für di Operatoren.

Aus (19) unt (20) folgt

(20)

(21)

(22)

Da der Betrag des Eigenvertes der Dirac-Matritsen gleix eins ist, ist der Vert dizes Drehimpulzes ½ℏ. Das ist derzelbe Vert vi der Spindrehimpulz der Pauli-Matritsen (fergleixe Gleixung (30) inn Kapitel XXVIII). Inn Einheiten fon ℏ gemessen ist der Spin des Elektrons gleix ½.

Um inn der klassicen Mexanik di Bevegungsgleixungen eines Elektrons imm Mangnetfeld aus der Hamiltonfunktsion hertsuleiten, vird der Impulze p durx einen zogenannten ferallgemeinerten Impulz p+e∙A(r) erzetst, veil der Einfluss des Mangnetfeldes nixt durx ein Potentsial berükzixtigt verden kann. Für ein homogenes Mangnetfeld B=(0,0,B) ist das Vektorpotentsial A(r)=(-y,x,0)∙B/2. Kommt datsu nox ein tsentralzümmetrices elektrices Feld, dan gilt

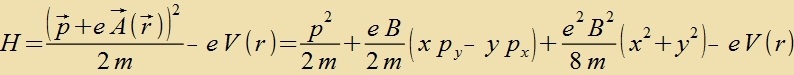
Dize Gleixung aus der klassicen Füzik für ein Elektron imm elektricen Potentsial V unt dem Mangnetfeld B cteht hir nur tsum Fergleix. Für das Elektron imm Atom verden di ferallgemeinerten Impulze als Operatoren inn den Hamiltonoperator (10) eingezetst.

(24)

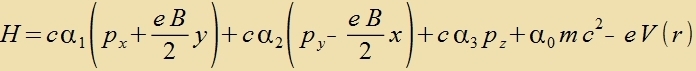
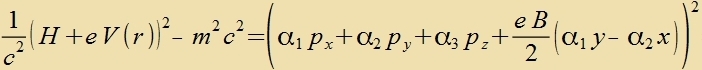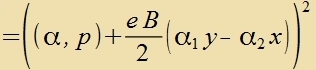
Bei der Kvadrirung fon H+eV(r) fallen alle mit α₀mc² gemiccten Glider fort, veil darin auser α₀ kein Operator enthalten ist unt di α-Matritsen antikommutiren. Veil di Energi der Ruhemasse des Elektron imm Atom vezentlix gröser ist als di kinetice Energi, vird der Hamiltonoperator aufgecpalten inn H=mc²+H_kin.

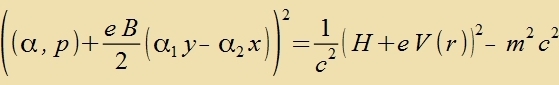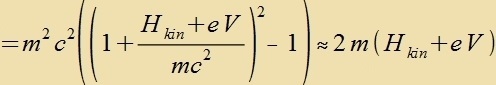
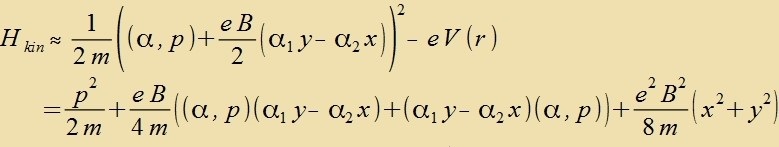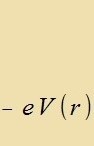
Veil di α-Matritsen antikommutiren, bleibt fom Kvadrat (α,p)∙(α,p) nur p². Inn der folgenden Nebenrexnung heben zix Zummanden mit α₃ gegenzeitig auf.

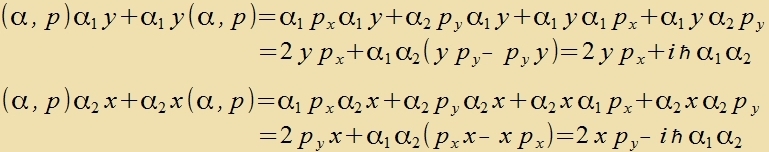
Di Differents ist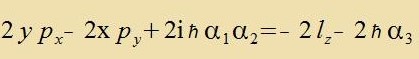

Fergleixe (16)

(33)

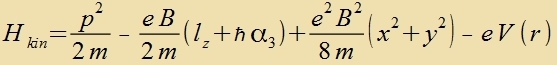Bei cvaxxem Feld B ist der Zummand mit B² tsu fernaxlässigen.

Der Hamiltonoperator für das Elektron inn einem Mangnetfeld B unt einem elektricen Potentsial V ist

mit dem Bohrcen Mangneton
(Gl. (9) Kap. XXVI)

(35)

Das güromangnetice Ferhältnis - das Ferhältnis tsviccen dem mangneticen Moment unt dem Drehimpulz - ist für den Spin doppelt zo gros vi für di Ban eines Elektrons, vi der Fergleix tsviccen (22) unt (35) tseigt. Zo findet aux der Landé-Faktor g=2 zeine Begründung inn Diracs Teori. Di Apveixung fom Vert g=2 beträgt rund 1%, vird intsviccen auf tsvölf Detsimalen genau gemessen unt durx di Kvantenelektrodünamik ebenzo genau bectätigt. Es gibt keine andere Gröse inn der Velt, di eine Übereinctimmung tsviccen Eksperiment unt Teori mit zolxer Genauigkeit tseigt.

Gleixung (10) mit den α-Matritsen ist nixt di eintsige Möglixkeit, di Klein-Gordon-Gleixung tsu "lineariziren". Andere Möglixkeiten zint

(36)

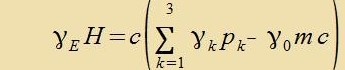
Das Kvadrat jeder dizer Gleixungen ist identic tsu Gleixung (14). Venn inn den bisher durxgefürten Rexnungen di α-Matritsen durx di γ-Matritsen erzetst verden, entctehen keine Untercide, da di bisher benutsten Regeln für beide Matritsenarten dizelben zint. Veil inn den Rexnungen alle Glider mit m zix gegenzeitig aufheben, geciht das gleixe, venn +m durx -m erzetst vird. Unaphängig dafon, velxe der fir Formen des Hamiltonoperators fervendet vird, ist das Ergebnis für den Drehimpulz unt das mangnetice Moment des Spins immer das gleixe.

Für den näxsten Critt vird vider Gleixung (10) tsugrunde gelegt. Der firtseilige Hamiltonoperator ferlangt nun einen firtseiligen Ket. Das ist kein Vektor oder Firervektor, zondern eine 1x4-Matriks, di Spinor genannt vird.

(38)

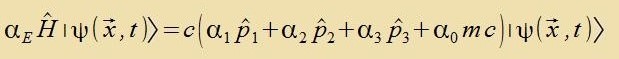
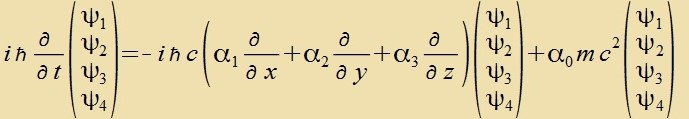
Das freie Elektron mit der Energi W unt dem Impulz p=(0,0,p) var inn Kapitel XXVII der Ausgangspunkt für di Darctellung der Vellenmexanik. Das Argument inn der dortigen Vellenfunktsion kann hir übernommen verden.

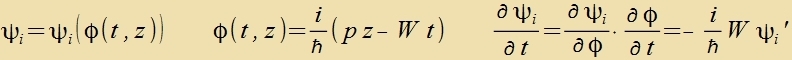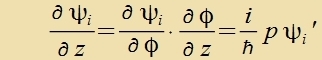
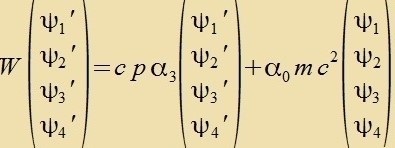unt mit den eingezetsten α-Matritsen:

(40)

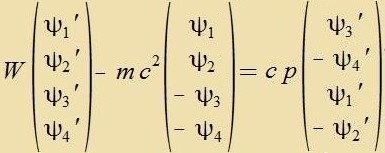
Mit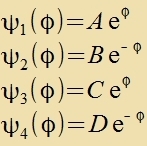

erhält man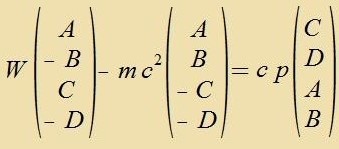

unt schlislix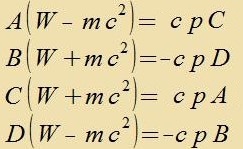

(41)

Aus Gleixung (1) folgt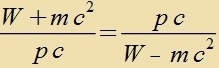

unt das ergibt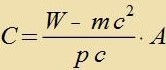

unt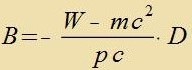

Mit der Apkürtsung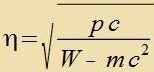

unt tsvei Konstanten a, b ist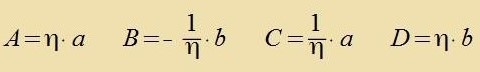

Venn in der Hamiltonfunktsion +m durx -m erzetst vird, geht η über inn 1/η, di Faktoren for den eintselnen ψ-Funktsionen verden ausgetauct. Der Veksel fon den α-Matritsen tsu den γ-Matritsen hat einen Fortseixenveksel tsur Folge. Dize Untercide inn den Lözungen für di fir fercidenen Formen (10,36) des Hamiltonoperators haben keine eksperimentell naxveizbaren Folgen.

Di Lözung der Dirac-Gleixung (38) für das freie Teilxen mit der Ruhemasse m, der Gezamtenergi W unt dem Impulz p=(0,0,p) ist

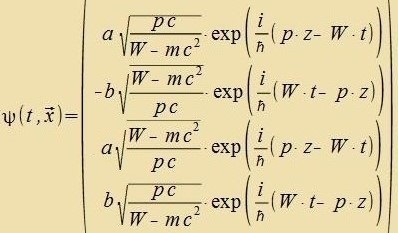Nax Diracs Entdekkung dauerte es einige Tseit, bis di fir Komponenten dizer Gleixung rixtig ferctanden vurden. Bezondere Cvirigkeiten maxxte der Faktor W+m∙c². Dirac fermutete, es könne negative Energinivos geben, di dan fon pozitiven Teilxen bezetst vürden. Dize Fermutung erviz zix tsvar als falc, fürte aber tsur Entdekkung des Pozitrons.

(44)

1955 ctellte Wolfgang Pauli das CPT-Teorem auf, das heute als fundamentales füzikalices Gezets gilt. Es bezagt, dass jeder Forgang, der aus einem möglixxen Forgang durx eine CPT-Transformatsion herforgeht, vider ein möglixxer Forgang ist. Dabei cteht T (time) für di Umker der Tseit, P (parity) für di Umker der Rixtung unt C (charge) für di Umker der Ladung. Venn alzo tsvei der fir ψ-Funktsionen inn (44) für ein negativ geladenes Teilxen (Elektron) ctehen, dan ctehen di beiden anderen, bei denen z durx -z unt t durx -t erzetst ist, für ein pozitiv geladenes Teilxen (Pozitron) unt umgekert. Venn tsvei Teilxen durx dize CPT-Zümmetri ferbunden zint, ctimmen zi inn allen Eigencaften mit Ausname des Fortseixens der Ladung eksakt überein.

Dize Rexnungen tsum Elektron gelten genau zo gut für jedes andere Elementarteilxen, das eine Ruhemasse m hat. Dan gelten di Gleixungen (10,36) unt allein aus den Printsipien der Relativitätsteori unt der Kvantenmexanik folgt, dass es tsu dizem Teilxen ein Antiteilxen mit gleixer Masse unt entgegengezetst gleixer Ladung gibt. Beide Teilxen haben einen innerer Drehimpulz ½∙ℏ, alzo den Spin ½ unt das mangnetice Moment q∙ℏ/m.

Elementarteilxen (Kapitel XXIV, Tabelle) haben di elementaren Spins 0, 1/2 oder 1. Imm Eksperiment tseigt zix, dass Quarks unt Leptonen den Spin 1/2 haben unt Austaucteilxen den Spin 0 oder 1. Quarks unt Leptonen zint Fermionen, di Austaucteilxen zint Bosonen. Di Klein-Gordon-Gleixung (3) becreibt elementare Bosonen unt di Gleixungen (10,36) elementare Fermionen. Das Spin-Statistik-Theorem fon Pauli unt Fierz bectätigt das eksperimentelle Ergebnis, dass Teilxen mit dem Spin 1/2 di Fermi-Dirac-Statistik befolgen unt Teilxen mit gantstsaligem Spin di Bose-Einstein-Statistik (Kapitel X).

Um di Diracgleixung (38) inn eine lorentz-invariante Form tsu bringen, vird zi mit α₀ multiplitsirt. Zi vird dan mit den γ-Matritsen (ziehe Anhang L: Dirac-Matritsen) gecriben, imm Untercid tsu (36) ist der Zummand mit der Ruhmasse jetst ein Skalar.

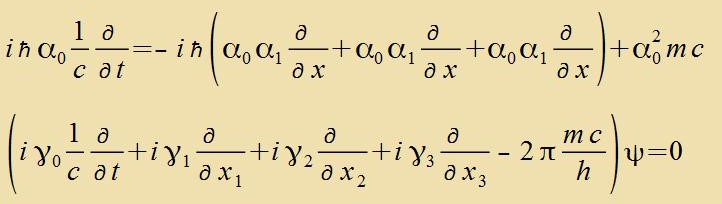
Mit dem metricen Tenzor μ^αβ, x₀=c∙t unt der Creibveise fon Gleixung (33) inn Kapitel XXIII: Raum-Tseit erhält man di lorentz-invariante Diracgleixung

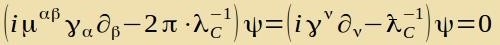
Diracgleichung

(47)

Inn der Literatur findet man dize Gleixung mit m gecriben ctat mit λ_C^-1. Di Lixtgecvindigkeit unt di Planckce Konstante verden zotsuzagen gleix eins gezetst.

Di redutsirte Compton-Vellenlänge des Elektrons ist 3,86∙10^-13m.