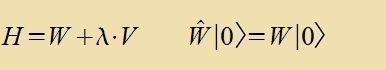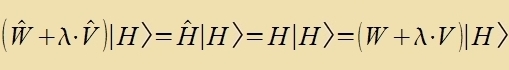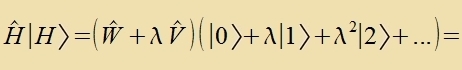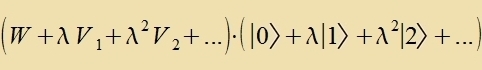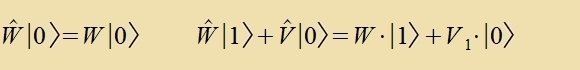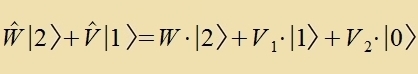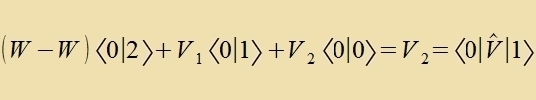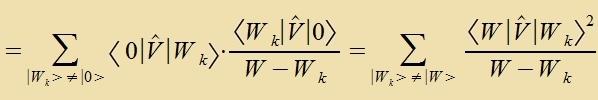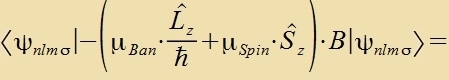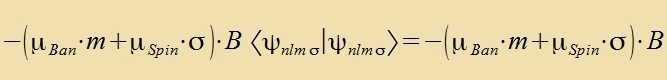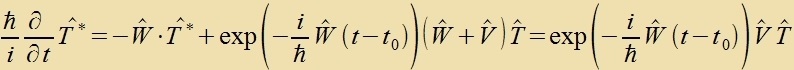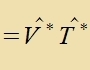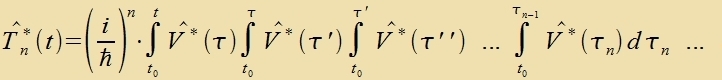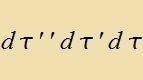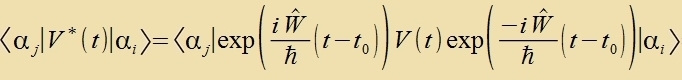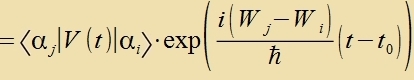Füzik

Home

XXIX. Tsuctand unt Ctörung

Porträ (bearbeitet) Fundctelle

	Venn Züsteme oder Tsuctände fon Züstemen zix one gegenzeitige Beeinflussung überlagern, vird dize Überlagerung matematic mit Mitteln der linearen Algebra becriben. Da es bei zolxen Überlagerungen auf den Fazenuntercid ankommt, rexnet man imm kompleksen Tsalbereix. Di Ergebnisse zolxer Rexnungen müssen aber reelle Verte zein fergleixbar tsu den reellen Verten fon Messergebnissen. Das Gleixe findet man inn einigen Bereixen der klassicen Füzik, beicpilsveize beim Vekselctrom, Lixt oder allgemein bei Vellen. Venn etva tsvei entgegengezetst laufende Vellentsüge zix überlagern, verden di Amplituden fazenrixtig addirt. Laufen di Vellentsüge dan vider auseinander, hat zix an irer Erceinung nixts geändert. Dize lineare Zuperpozitsion ist ein grundlegendes Printsip inn der Kvantenmexanik unt gilt gleixermasen für Tsuctände vi für Operatoren. Dirac hat getseigt, dass Schrödingers Vellenmexanik unt Heisenbergs Matritsenmexanik tsvei Zeiten derselben Medalje zint. Opzervable verden durx Operatoren dargectellt; das zint bei Schrödinger Differentsialoperatoren, bei Heisenberg Matritsen. Di Differentsialoperatoren virken auf Funktionen, di Matritsen auf Vektoren. Operatoren haben Eigenverte unt tsu jedem Eigenvert gehört ein cpetsieller Tsuctand des Züstems, der bei Schrödinger durx eine Eigenfunktsion des Differentsialoperators, bei Heisenberg durx einen Eigenvektor der Matriks dargectellt vird. Dirac hat mit zeinen Bra- unt Ketvektoren eine Creibveize für den kompleksen Hilbertraum eingefürt, di gleixermasen für Schrödingers Vellenmexanik vie für Heisenbergs Matritsenmexanik cteht. Tsvei Eigenfunktsionen oder Eigenvektoren, di zix nur um einen konstanten Faktor unterceiden, becreiben denzelben Tsuctand, veil zi tsum gleixen Eigenvert gehören. Erst venn tsvei untercidlixe Tsuctände überlagert verden, bectimmen di Faktoren, mit velxen Anteilen unt mit velxer Faze di Zummanden ins Ergebnis eingehen. Di Mathematik imm Raum der Ketvektoren vird becriben imm Anhang K: Bra unt Ket. Der Ervartungsvert ‹A› einer Opzervablen kann durx äusere Bedingungen beeinflusst verden, venn di ctatistice Ferteilung der Tsuctände tsum Beicpil einer termodünamic bedingten Ferteilung der Energinivos folgt. Inn einem Ensembel gleixer Teilxen zei pn di Varceinlixkeit, ein Teilxen imm Tsuctand ∣αn> antsutreffen. Dan ist der Ervartungsvert der Opzervablen A für das Ensembel 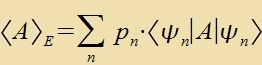oder mit dem Einheitsoperator 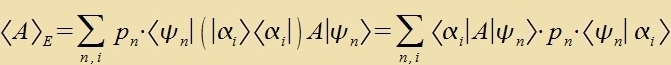(1) Mit einem Dixteoperator 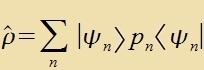erhält man 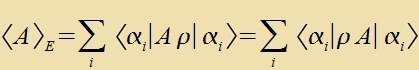Di Ctellung fon pn inn Gleixung (1) ist belibig unt der Operator A kann for oder nax dem Einheitsvektor ctehen. Daraus folgt di Fertaucbarkeit fon ρ unt A. Fon dizen ctatistic gemiccten Tsuctänden müssen kohärent ferbundene Tsuctände unterciden verden (Lezer, Fercränkung). Da di meisten kvantenmexanicen Probleme nixt eksakt lözbar zint, cpilt di Ctörungsrexnung eine grose Rolle. Datsu muss di Hamiltonfunktsion H tserlegt verden können inn einen Teil W, der eine eksakte Lözung ∣W>=∣0> hat, unt eine Ctörungsterm V, der klein ist gegenüber W. Imm einfaxxsten Fall ist der Eigenvert fon W nixt entartet unt unt V nixt tseitaphengig. Als beobaxtbare Gröse hat H eine Eigenfunktsion ∣H> imm Eigenraum fon W, unt inn dizem Raum vird ∣H> inn eine Potentsreihe λn∣n> mit reellen Tsalen λ unt Einheitsvektoren ∣n> entvikkelt. Ebenzo zoll der Eigenvert H entvikkelt verden. 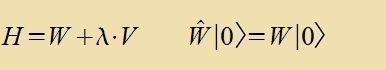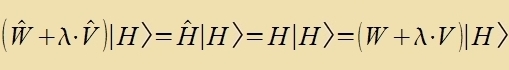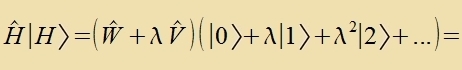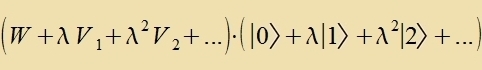Eine Zortirung nax der Ordnung inn λ ergibt	(4) (5)
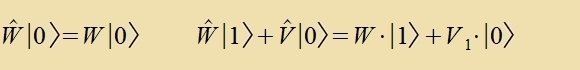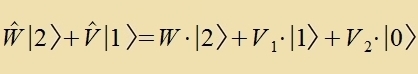
	Multiplitsirt man di tsveite Gleixung fon links mit <0∣, dan erhält man di Korrektur erster Näherung V1 für das Energinivo W. Inn erster Näherung vird das nixt entartete Nivo durx di Ctörung nixt aufgecpalten, zondern fercoben, unt di Fercibung ist gleix dem Mittelvert des Ctörpotentsials über di ungectörte Ban. Das entcprixxt imm übrigen der klassicen Ctörungsteori. Tsur Berexnung der tsveiten Näherung ist es nötig, den Vektor ∣1> nax den Bazisvektoren ∣Wk> imm Eigenraum des Operators W tsu entvikkeln. Veil di Gleixung (4) unferändert bleibt, venn man tsu ∣1> einen Vektor κ∣0> hintsu addirt, kann ∣1> fon forneherein zo gevält verden, dass <0∣1>=0 ist. 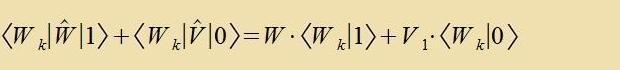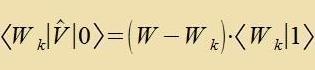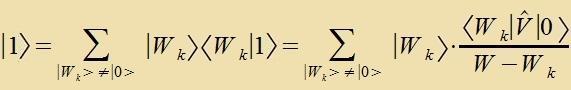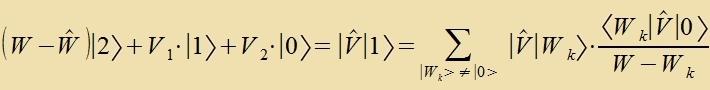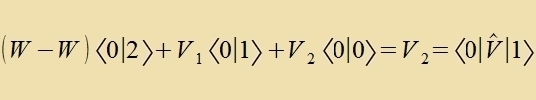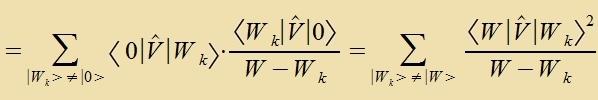Für ∣Wk> ≠ ∣0> folgt aus (5b) Mit dizer Betsihung erhält man di Entvikklung des Vektors ∣1> imm Eigenraum fon W Di Entvikklung vird inn Gleixung (5c) eingezetst Das Ctörpotentsial V fercibt das Nivo W inn 1. unt 2. Näherung insgezamt um 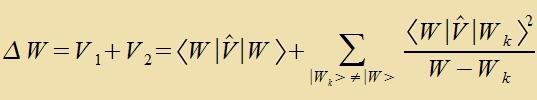Imm Ergebnis ist ∣0> durx ∣W> erzetst. Di Potentsialdifferents E∙z eines elektricen Feldes E=(0,0,E) längs einer Ctrekke s=(x,y,z) ertseugt di Ctörenergi V=-e∙E∙z für di Vellenfunktsion Ψn,l,m(r,θ,φ). Inn erster Näherung	(12)
	Veil f(θ)=Q²(cos θ) als Zumme über ci∙sin2∙i(θ) gecriben verden kann (fergleixe Kapitel XXVII, Gleixungen (39) ff), ist f(θ)=f(π - θ). Di Parität fon f(θ) ist gerade unt das Gleixe gilt für f(θ)∙cos(θ). Für den Integranden imm letsten Integral g(θ)=f(θ)∙sin(θ)∙cos(θ) folgt g(θ)=-g(π - θ). Deshalb ist das letste Integral gleix Null, es gibt keine Ctörung erster Näherung durx ein elektrices Feld, veil das Atom kein elektrices Dipolmoment bezitst. Der Mittelpunkt der negativen Ladungsferteilung fällt mit der pozitiven Ladung imm Kern tsuzammen. Inn tsveiter Näherung 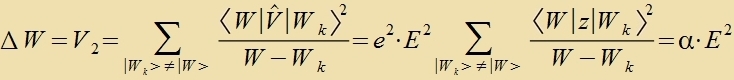Dis ist der kvadratice Stark-Effekt. Inn klassicer Zixt tsiht das elektrice Feld di pozitive unt negative Ladung auseinander unt ertseugt zo ein elektrices Dipolmoment (Polarizatsion), das dan imm elektricen Feld eine potentsielle Energi annimt. Di potentsielle Energi eines mangneticen Dipols μ imm homogenen Mangnetfeld B=(0,0,B) ertseugt ein Ctörpotentsial V=-μz∙B (Gl. (13) inn Kapitel XVII). Imm einfaxxsten Fall, venn nur ein Elektron berükzixtigt verden muss, zetst zix das mangnetice Moment tsuzammen aus dem des Bandrehimpulzes μBan unt dem des Spins μSpin. 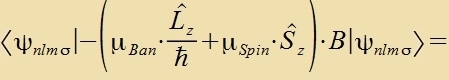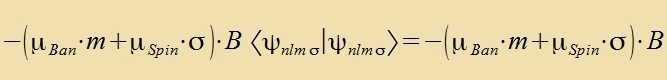Da di Operatorkomponenten Lz unt Sz mit der Hamiltonfunktsion fertaucbar zint, gilt für di Ctörung inn erster Näherung Veil bei der Emission das Foton den Drehimpulz ℏ mitnimt, gilt für di Emission fon Lixt di Ausvalregel Δl=∓1 (Kapitel XXVI, Gl.(a)). Dabei kann m zix höxstens um eins ändern (Δm=-1,0,+1), di Einctellung des Spins ändert zix nixt. Veil alle Nivos durx den Beitrag des Spins um denzelben Betrag apgezenkt verden, ist dizer Beitrag imm Cpektrum nixt erkennbar. Di Linie für den Übergang fom (one Feld entarteten) Nivo n=2 tsu n=1 cpaltet daher inn drei äkvidistante Linien auf. Aus dizem Apctand, der proportional tsum Mangnetfeld B ist, vird das mangnetice Dipolmoment des Bandrehimpulzes bectimmt. Entcprexxende Ergebnisse gelten für di Apzorptsion unt für Übergänge mit anderen Hauptkvantentsalen. Normaler Zeeman-Effekt Übergang Δn=∓1 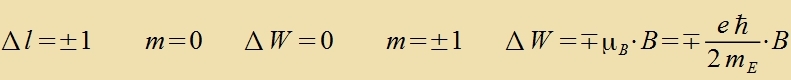μB ist das Bohrce Mangneton (Gl. (9) inn Kap. XXVI). Beim anomalen Zeemann-Effekt - der veit häufiger ist - muss der Gezamtdrehimpulz aus den zummirten Bandrehimpulzen unt den zummirten Spin-Drehimpulzen gebildet verden. Nax dem Eintritt einer konstanten Ctörung ctellt zix ein Züstem entcprexxend ein unt bleibt dan ctationär. Venn di Ctörung tseitaphengig ist, muss für di Reaktsion eines Züstems eine andere Art der Ctörungsrexnung angevendet verden. Der Hamiltonoperator H zetst zix vider tsuzammen aus dem Operator W für den ungectörten Tsuctand unt dem Ctöroperator V. Di tseitaphengige Schrödingergleixung vird jetst inn das Heisenberg-Bild übertragen, indem di tseitlixxe Feränderung eines Tsuctandes durx einen Operator T dargectellt vird. Vird dize Änderung inn dem oben becribenen Koordinatenzüstem Kα dargectellt, das fest ist unt inn dem jede Entartung aufgehoben ist, dan ferändert di Ctörung di Varceinlixkeitsamplitude ci. 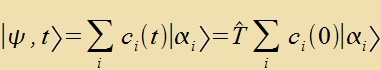Di Änderung der Varceinlixkeitsamplituden bedeutet: Der Operator T ertseugt Übergänge tsviccen den Bazisvektoren. 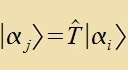Der Operator T ist aphängig fon der Tseit t, er becreibt di tseitlixxe Envikklung eines Züstems. T hat keine Eigenverte (auser der eins für t=0) unt cteht daher nixt für eine Opzervable, muss alzo nixt hermitec zein. Aux di Tseit t ist hir keine Opzervable, zondern eine Variable vi inn der klassicen Füzik. 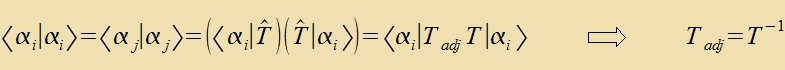Da di ∣αk> normirt zint, folgt Ein Operator, der tsu zeinem Inverzen adjungirt ist, heist inn der Matematik unitär. Den unitären Operatoren entcprexxen imm Reellen di ortogonalen Koordinatentransformatsionen. Di tseitlixxe Entvikklung des Dixteoperator ist 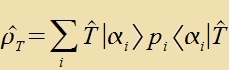unt di Varceinlixkeit, ein Züstem imm Tsuctand ∣αj> tsu finden, ist nach Aplauf der Tseit t:	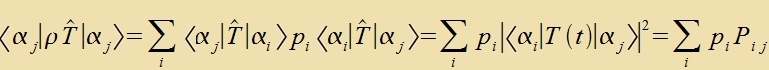(22)
	Der Zummand mit i=j ist di Varceinlixkeit, dass ein Züstem urcprünglix imm Tsuctand ∣αj> var unt keinen Übergang maxxt, di anderen Zummanden tseigen di Varceinlixkeiten, dass ein Züstem urcprünglix imm Tsuctand ∣αi> var unt inn der Tseit t inn den Tsuctand ∣αj> übergeht. Aus der tseitaphengige Schrödingergleixung (Gl. (2a) inn XXVII) erhält man eine Differentsialgleixung für den Tseitentvikklungsoperator T(t). 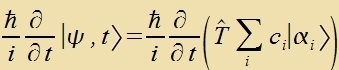unt 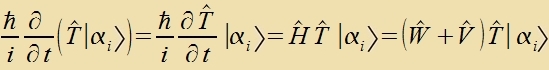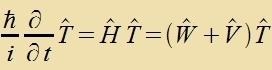ist di Differentsialgleixung für den Tseitentvikklungsoperator. 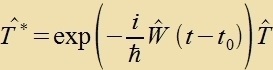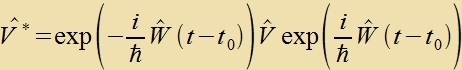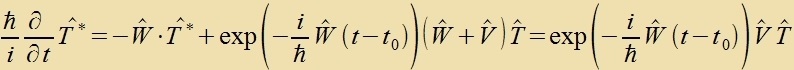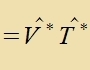Mit unt erhält man eine einfaxxere Gleixung Tsum Tseitpunkt t=t0 zint di Operatoren T unt T* beide gleix dem (tseitunaphengigen) Einheitsoperator E. Da di Apveixung tsviccen T* unt E kurtse Tseit cpäter als gering angezehen verden kann, vird T* auf änlixxe Veize vi bei der Näherung der teitunaphängigen Ctörung entvikkelt. Fon erster Näherungsordnung zeien alzo T*1 unt V*, fon tsveiter Ordnung T*2 unt V*T*1 unt zo veiter. 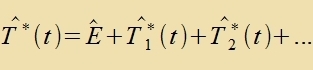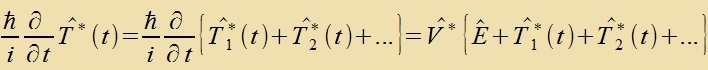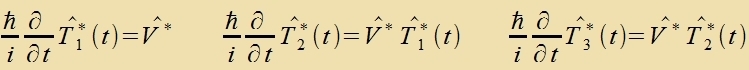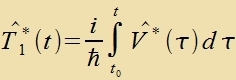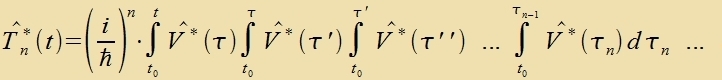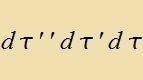Nax der Ordnung der Näherung zortirt Venn ein konstantes Ctörpotentsial bei t=t0 einzetst oder das Ctörpotentsial fon t0 bis t praktic kontant bleibt, dan gilt 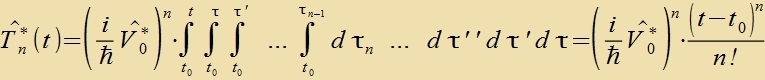Dize Reihen zint fon gleixer Form vi di Reihen für eix unt e-ix, ir Produkt ergibt den Einheitsoperator. Der tsu T*(t) adjungirte Operator ist daher inverz tsu T*(t), T*(t) ist unitär. 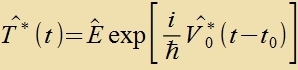Man creibt In erster Näherung	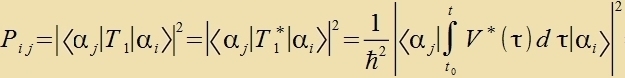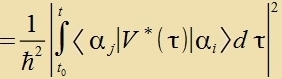(33)
	Veil das Ctörpotentsial eine Opzervable ist, ist der Operator V hermetic unt ebenzo V*. Nun gilt für tsvei reelle Funktsionen 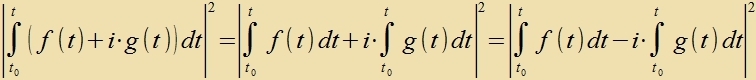Daraus folgt 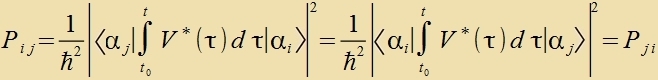Unter dem Einfluss einer Ctörung ist di Übergangsvarceinlixkeit tsviccen tsvei Tsuctänden inn beiden Rixtungen dizelbe, Emission unt Apzorptsion zint gleix varceinlix - ziht man ap fon den Bezetsungstsalen (pi). Dize ctimulirte Emission vurde zer früh fon Einstein erkannt, zi cpilt di fundamentale Rolle beim Lezer. Der Integrand inn Gleixung (33) vird veitergerexnet, indem der erste unt letste Faktor auf den Bravektor betsihungsveize den Ketvektor angevendet verden. 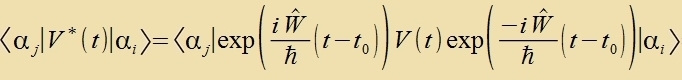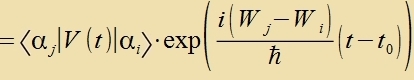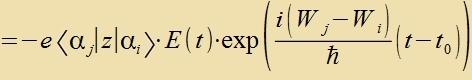Hir ist das Ctörpotentsial V(t)=-e∙E(t)∙z des elektricen Feldes einer elektromangneticen Velle eingezetst vorden. Es ist 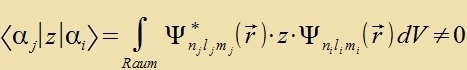nur venn 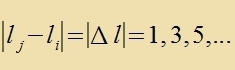Damit das Matrikselement nixt gleix Null vird, muss di Funktsion Ψj(r)∙z∙Ψi(r) fon gerader Parität zein (fergleixe (53) inn Kapitel XXVII), Ψj(r)∙Ψi(r) muss alzo ungerade Parität haben. ∣Δl∣>1 vürde bedeuten, dass di Änderung des Drehimpulzes gröser als ħ väre, ein zolxer Drehimpulz kann aber bei der einfaxxen Dipolctralung nixt fon einem Foton übernommen verden. Di notvendige Bedingung für dizen Übergang ist alzo ∣Δl∣=1. Daraus folgt veiter, dass aux ∣Δm∣ nixt gröser als eins zein darf; denn dan väre ∣Δl∣ mindestens ebenzo gros. Δm=0 ist ebenfalls möglix, es bedeutet, dass der Drehimpulz zix zenkrext tsur z-Rixtung ändert. Δm bectimmt di Polarizatsion des Fotons. Clislix erhält man 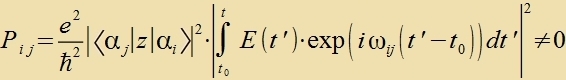nur für ∣Δl∣=1 unt	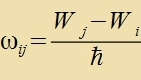(40)
	Di Übergangsvarceinlixkeit tsviccen tsvei Nivos mit den Energien Wi unt Wj vird bectimmt durx di Fourierkomponente - das Integral inn Gleixung (40) - der einfallenden Ctralung mit der Frekvents νij=(Wi-Wj)/h. Nur durx dize Komponente verden Übergänge feranlast. Damit ist das entcprexxende Bohr'ce Postulat kvantenmexanic begründet. Inn 2. Näherung ist 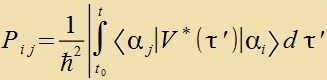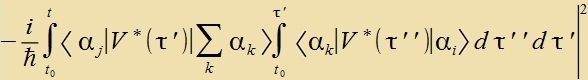Beim Übergang fon ∣αi> nax ∣αj> kommen inn der tsveiten Näherung alle ∣αk> als Tsviccentsuctände for.
A