Für di Becreibung kvantenmexanicer Tsuctände hat Dirac di Ket-Vektoren eingefürt. Di Vektoren des datsu dualen Vektorraumes zint di Bra-Vektoren, zodas di Klammer (bracket) das Skalarprodukt darctellt. Parallele Vektoren becreiben denzelben Tsuctand, veil di lineare Zuperpozitsion eines kvantenmexanicen Tsuctandes mit zix zelpst nur vider denzelben Tsuctand ergeben kann. Faktoren for einem Tsuctandsvektor haben daher keine Bedeutung für den Tsuctand, vol aber bei der Zuperpozitsion. Veil imm allgemeinen di Tsal der Eigenverte unt Eigenvektoren eines Operators unendlix ist, muss inn einem Hilbertraum über den kompleksen Tsalen gerexnet verden. Hir verden keine Kentnisse des Hilbertraumes forausgezetst, da di hir nötigen matematicen Verktseuge zix nixt fon denen eines endlixxen Vektorraumes unterceiden. Auf den Fall kontinuirlixxer Eigenverte (t. B. freies Elektron) vird nixt eingegangen.

Ket: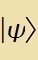

Bra: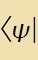

Skalarprodukt: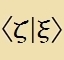

Normkvadrat: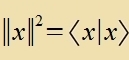

Skalarprodukt unt Normkvadrat zint Tsalen. Veil di Norm reell unt auser für den Nullvektor pozitiv zein zoll, müssen di Linearitätsregeln für das Skalarprodukt angepasst verden. Der Ctern^* an einer Tsal bedeutet den konjugirt-kompleksen Wert.

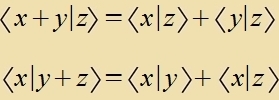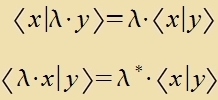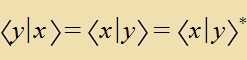Das Skalarprodukt ist zümmetric unt reell.

Dize Regeln gehen über inn di des reellen Vektorraumes, venn alle Tsalen reell zint.

Das Skalarprodukt der Tsuctandsvektoren tsveier Vellenfunktsionen ζ(r) unt ξ(r) ist das Integral fon ζ^*(r)⋅ξ(r) über den Definitsionsbereix. Das Integral eksistirt, venn beide Funktsionen kvadrat-integrirbar zint, unt genügt den formulirten Regeln.

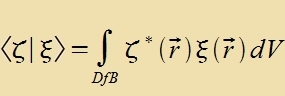Alle bisher behandelten Vellenfunktsionen zint kvadrat-integrirbar.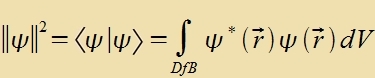

Bei Vellen der klassicen Füzik gibt das letste Integral di Gezamtintenzität der Velle an, bei geringerem Integratsionsvolumen den Anteil der Intenzität. Der klassicen Intenzität entcprixxt inn der Kvantenmexanik di Varceinlixkeit, das Teilxen antsutreffen. Ein Teilxen, das inn einem bectimmten Tsuctand ist, ist mit Zixxerheit, alzo mit der Varceinlixkeit eins irgendvo imm Raum. Deshalb vird di Vellenfunktsion entcprexxend normirt, zi bekommt einen Faktor, zodas ire Norm gleix eins vird.


Di bisher behandelten Vellenfunktsionen zint imm Anhang mit irem Normirungsfaktor dargectellt, Rexnungen datsu verden nur an cpetsiellen Beicpilen durxgefürt. Imm folgenden verden alle Vellenfunktsionen unt allgemein alle Tsuctandsvektoren als normirt angenommen.

Lineare Operatoren verden inn einem Vektorraum durx Matritsen dargectellt. Virkt ein Operator auf einen Ket, zo vird di Operator-Matriks fon links mit dem tsum Ket gehörenden Cpaltenvektor multiplitsirt. Virkt ein Operator auf einen Bra, dan vird dizer als Tseilenvektor gecriben unt fon links mit der Matriks multiplitsirt. Das zint tsunäxst tsvei fercidene Matritsen, di tsu einander adjungirt zint, venn zi tsum gleixen Operator gehören. Um den Tsuzammenhang tsviccen einer Matriks A unt irer Adjungirten A_adj tsu finden, vird das folgende Skalarprodukt unterzuxt.

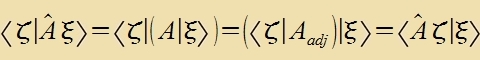
Um aus der Matriks A di Adjungirte tsu gevinnen, ist der gleixe Übergang vi fom Ket tsum Bra nötig: Tseilen unt Cpalten verden ausgetauct. Zo erhält man di Transponirte A^T mit den Einträgen a^T_jk=a_kj. Bei reellen Matritsen ist di Adjungirte di Transponirte, nixt aber bei kompleksen Matritsen.

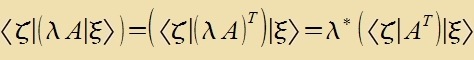
Venn nun inn der Transponirten alle Einträge durx ire konjugirt-kompleksen Verte erzetst verden, erhält man di adjungirte Matriks A_adj=A*^T. Vixtig für di Kvantenmexanik zint di zelpst-adjungirten Matritsen, alzo Matritsen, für di A=A_adj gilt. Zelpst-adjungirte Matritsen verden hermitec genannt. Hermitec zint alzo di Matritsen, di ungeändert bleiben, venn alle Einträge durx ire konjugirt-kompleksen Verte erzetst unt an der Hauptdiagonalen gecpigelt verden: a_jk=a*_kj. Zumme unt Produkt tsveier hermitecer Matritsen zint vider hermitec. Man kann unendlixxe Reihen bilden unt erhält auf dize Veize Funktsionen, di den holomorphen Funktsionen entcprexxen.

Im folgenden zeien alle Matritsen hermitec. Das unterzuxte Skalarprodukt kann dan one Klammern gecriben verden.

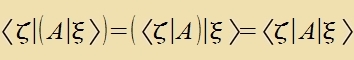Das fürt tsu tsvei vixtigen Folgerungen.

Ist α ein Eigenvert eines Operators, dan gilt

zovol als aux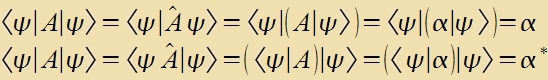

Veil α=α* ist, zint di Eigenverte hermitecer Matritsen reell.

Zint ∣β> unt ∣γ> tsvei Eigenvektoren der Matriks A mit den Eigenverten b unt g, dan gilt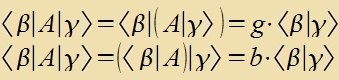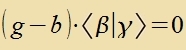

Das Skalarprodukt ist Null, venn b≠g ist.

Da das Skalarprodukt der beiden Eigenvektoren fercvindet, zint Eigenvektoren einer hermitecen Matriks ortogonal. Zi zint di Einheitsvektoren eines kartezicen Koordinatenzüstems imm Eigenraum dizer Matriks, di inn dizem Koordinatenzüstem diagonal ist mit den Eigenverten inn der Hauptdiagonalen. Veiter gilt für fercidene Operatoren:

Venn imm gemeinzamen Eigenraum der Operatoren A unt B jeder Eigenvektor fon A aux Eigenvektor fon B ist, dan zint A unt B fertaucbar. Venn A unt B fertaucbar zint, dan gilt für jeden Eigenvektor ∣ψ> fon A, dass aux B ∣ψ> Eigenvektor fon A ist unt umgekert.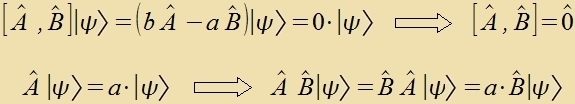

(10) (11)

Das direkte Produkt V = V_A X V_B der Eigenräume tsveier Operatoren A unt B ist der gemeinzame Eigenraum fon A unt B. Venn A unt B fertaucbar zint, dan bilden di Eigenvektoren fon A unt B  ein ortonormales Koordinatenzüstem fon V. Zo gibt es tsu jeder Menge fertaucbarer Operatoren einen gemeinzamen Eigenraum mit einer ortonormalen Bazis unt inn dizem Koordinatenzüstem verden di Operatoren durx diagonale Matritsen dargectellt. Zint di Ketvektoren ∣α_i> di Bazisvektoren dizes 'follctändigen' Koordinatenzüstems, dan vird ein allgemeiner Tsuctand ψ dargectellt durx

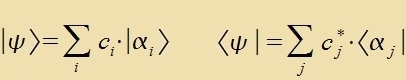mit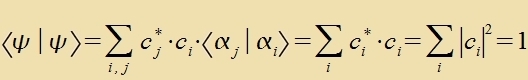

(12)

Di Koeffitsienten c_i zint 'Varceinlixkeitsamplituden', unt da di Zumme der Betragskvadrate gleix eins ist, erfüllen di ∣c_i∣² di Bedingung für Varceinlixkeiten.

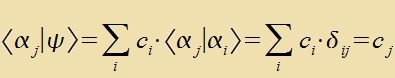Man erhält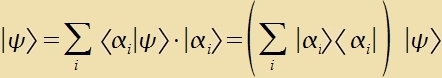

(13)

Vi üblix gevinnt man di Koeffitsienten für di Entvikklung eines Vektors, indem man in auf di Bazisvektoren projitsirt. Di letste Gleixung tseigt, dass der eingeklammerte Ausdrukk eine cpetsielle Form des Einheitsoperators ist.

Der Ervartungsvert ‹A› für eine Opzervable A mit den Eigenverten A_i ist

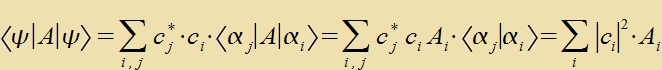Di möglixxen Verte verden gevixtet mit den Varceinlixkeiten. ‹A› ist unaphengig fom Koordinatenzüstem.

Tsurük tsu Kapitel XXVIII. Operatorenmexanik oder tsu Kapitel XXIX. Tsuctand unt Ctörung