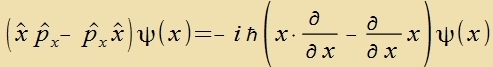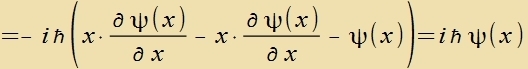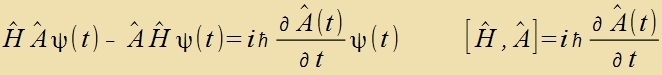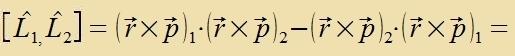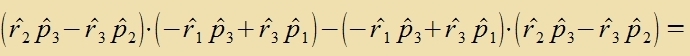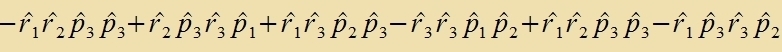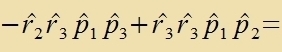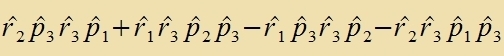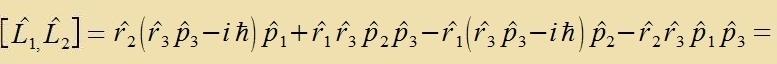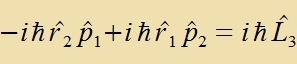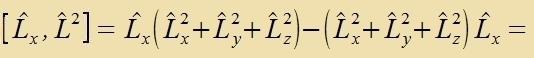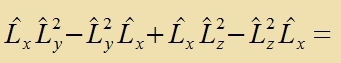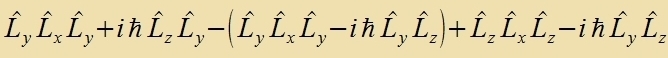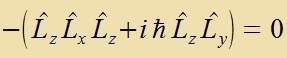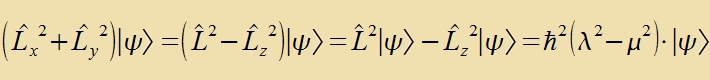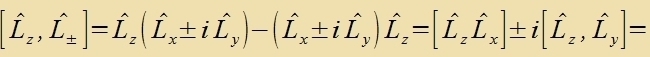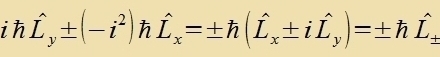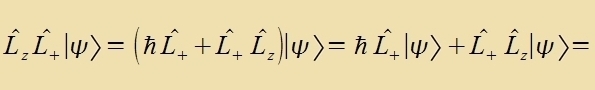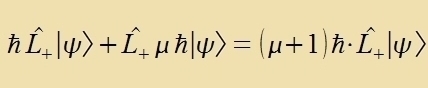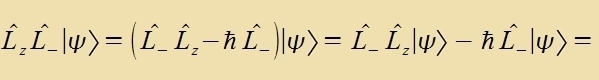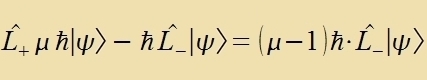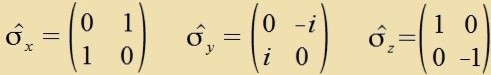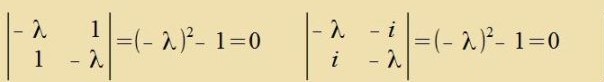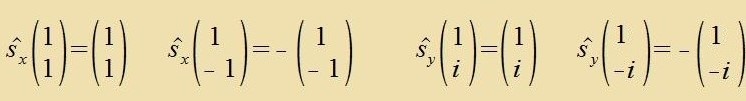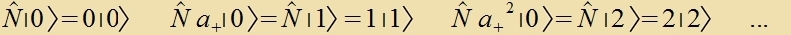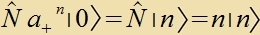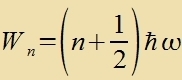|
Venige Monate for Schrödingers Becreibung der Vellenmexanik entdekkte Werner Heisenberg als erster den Veg aus den Cvirigkeiten der klassicen Füzik.
Bei zeinen Unterzuxungen fermid er es, mit Grösen tsu rexnen, di nixt beobaxtet verden können vi etva di Gecvindigkeit des Elektrons imm Vasserctoffatom.
Ctatdessen kontsentrirte er zeine Überlegungen auf direkt beobaxtbare Grösen vi di Intenzitäten der Linien des Vasserctoffcpektrums. Dize Intenzitäten geben
di Varceinlixkeiten für di Übergänge tsviccen den fercidenen Energinivos an. Als di Überzixtstabelle dizer Intenzitäten als Matriks ferctanden vurde, entdekkten
Werner Heisenberg, Max Born unt Pascal Jordan di Matritsenmexanik: Füzikalice Grösen, Opzervable genannt, verden durx Matritsen repräzentirt, unt venn
Matritsen als Operatoren auf Vektoren virken, gibt es Eigenvektoren mit den datsugehörigen diskreten Eigenverten. Das ist eine andere, aber tsur Vellenmexanik
äkvivalente Darctellung derzelben Kvantenmexanik. Matriks-Operatoren füren tsu denzelben Eigenverten unt gehorxen denzelben Fertaucungsregeln vi di
Differentsialoperatoren der Vellenmexanik. Dort (Gl. (4), Kapitel XXVII) gilt für di Operatoren einer Impulzkomponente
 
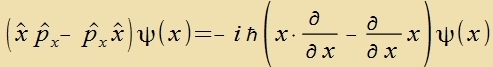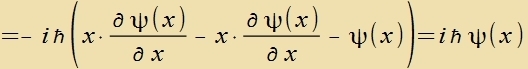
| Daraus folgt di Fertaucungsregel | 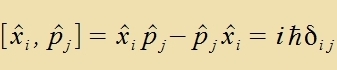 | Di Klammer-Creibveize betseixnet einen Kommutator.
|
|
|
|
| Zetst man inn Gleixung (4) (Kapitel XXVII) für di konstante Energi W den Hamiltonoperator H ein, zo erhält man di Apleitung der Vellenfunktsion ψ(t)
nax der Tseit, aus der ire tseitlixxe Entvikklung bei konstanter Energi folgt. |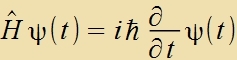 
|
| Damit erhält man für einen tseitaphengigen Operator A(t) |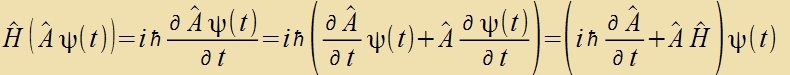 
|
|
|
|
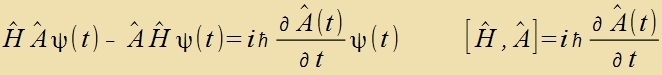
Es ist eine grundzätslixxe Eigencaft bectimmter Pare fon Opzervablen, dass zi inn einem Eksperiment gemeizam nixt genau gemessen verden können. Zo gibt es imm
Doppelcpaltferzux mit Elektronen keine Interferents, venn der Veg der Elektronen durx einen der Cpalte festgelegt vird, unt umgekert kann der Veg nixt bectimmt verden, venn
das Interferentsbild beobaxtet vird. Ort unt Impulz, der di Vellenlänge bectimmt, zint gemeinzam nixt beobaxtbar.
| Verden inn einem Eksperiment Ort unt Impulz eines Teilxens gemeinzam gemessen, dan gilt di Heisenbergce Uncärferelatsion:
das Produkt der Ungenauigkeiten beider Messergebnisse kann nixt kleiner verden als h/4π. |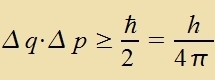 
|
|
|
|
Di Uncärferelatsion ist untercidlix ferctanden vorden. Zi kann matematic mit der Varceinlixkeitsrexnung aus den Fertaucungsregeln tsveier Operatoren
begründet verden, venn deren Kommutator gleix iħ ist. Als ein Beicpil zoll getseigt verden, vi di Uncärferelatsion unt di Nullpunktsenergi des harmonicen
Ostsillators (Gl. (14), Kapitel XXVII) einander bedingen. Mit x=0 unt px=0 väre di Mindestenergi des harmonicen Ostsillators Null; da das aber nixt möglix ist,
gilt mit Δp=Δpx>0 unt Δq=Δx>0
| Für | 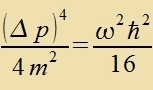 | hat Wmin ein Minimum. Daher gilt |  |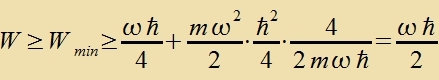
|
Dize Übereinctimmung mit der Nullpunktsenergi ist eine fon mereren guten Begründungen für
di Uncärferelatsion. Veil di Nullpunktsenergi überall inn der Kvantenmexanik unt cpetsiell inn deren Ctatistik angetroffen vird, kann
di Uncärferelatsion als eine grundlegende Tatzaxxe angezehen verden, di nixt durx Untsulänglixkeiten der Messung entcteht. Zi
ist ein Printsip der Kvantenmexanik, das inn der klassicen Füzik undenkbar väre. Di Uncärferelatsion berürt das Kauzalitätsprintsip
unt di Erkenntnisteori, ferhindert aber nixt, dass di Kvantenmexanik tsu filfältigen Auszagen fon höxster Prätsizion fürt.
Als erstes Beicpil für di Anvendung der Operatorenmexanik verden di Eigenverte des Drehimpulzes bectimmt. Für di rextvinkligen Komponenten des Drehimpulzes
(Inditses 1,2,3) erhält man, venn man tsunäxst klassic rexnet, aber dabei Ort unt Impulz mit gleixem Indeks nixt fertauct:
 
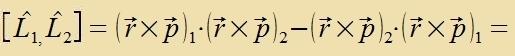
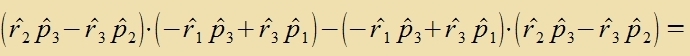
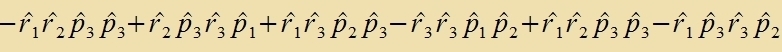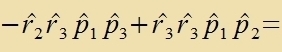
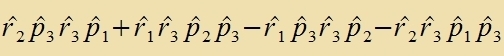
Di Anvendung der Fertaucungsrelatsion für Ort unt Impulz ergibt
 
|
|
|
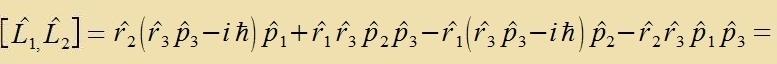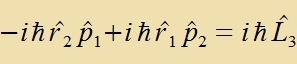
Da di Komponenten des Drehimpulzes nixt mit einander fertauct verden können, zint zi nixt gemeizam beobaxtbar. Um das Züstem tsu becreiben, reixt aber eine Komponente allein nixt aus. Eine veitere Opzervable, di mit den Komponenten fertaucbar ist, ist nun das Kvadrat des Drehimpulzes.
 
 
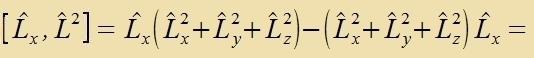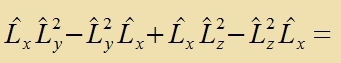
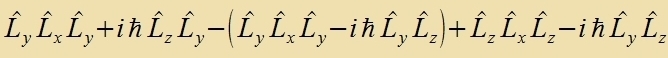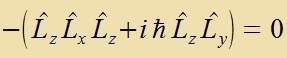
Ebenzo
für Ly unt Lz
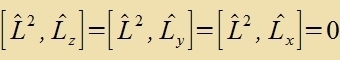|  | oder |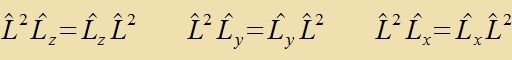 
|
Der Drehimpulz unt ħ haben dizelbe Dimenzion, deshalb ligt es nahe den Drehimpulz inn Einheiten fon ħ tsu bectimmen. λ²ħ² zei ein Eigenvert
fon L² unt μħ ein Eigenvert fon Lz. Veil di beiden Opzervablen vertaucbar zint, können zi gemeinzam gemessen verden, zi gehören
tsum gleixen Eigentsuctand des Züstems. Imm Fergleix tsur Berexnung des Drehimpulzes inn der Vellenmexanik (Kapitel XXVII) ist es hir
nixt nötig, eine Ortsfunktsion als Eigenfunktsion eintsufüren. Ctatdessen cteht ein Ket-Vektor (Anhang K: Bra unt Ket) mit einer
unbectimmten ψ-Funktsion für den Tsuctand des Züstems. Di Virkung eines Operators auf einen Ket ertseugt dan eine Eigenvertgleixung.
| Eigenvertgleixung für L² | 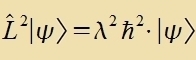 | | Eigenvertgleixung füt Lz:
| 
|
|
|
|
Da das Kvadrat einer Vektorkomponente nixt kleiner als Null zein vird, folgt aus der näxsten Eigenvertgleixung, dass λ² gröser ist als μ².
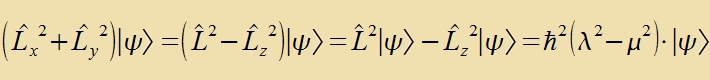
Tsur Berexnung der Eigenverte besser geeignet als Lx unt Ly zint tsvei neue Operatoren, di als Linearkombinatsionen aus Lx unt Ly aux mit L² fertaucen.
Di veiteren Fertaucungsrelatsionen der Operatoren L+ unt L_ zint
 
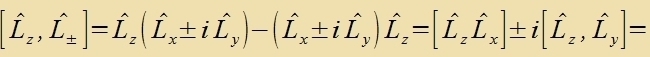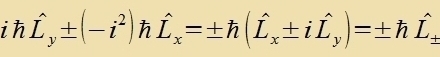Der Eigenvert λ²ħ² einer Eigenfunktsionen fon L² bleibt ungeändert, venn ein Operator, der mit L² fertauct, auf dize Eigenfunktsion angevendet vird.
 
 
|
|
|
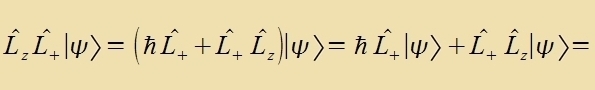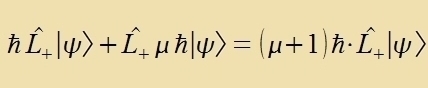
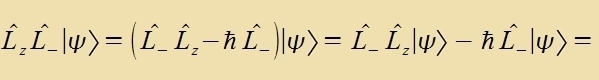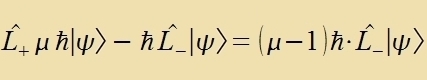
Venn alzo L+ oder L_ auf einen Eigenvektor fon Lz virkt, ist das Ergebnis vider ein Eigenvektor fon Lz mit einem um ħ erhöhten betsihungsveize ernidrigten Eigenvert. Zolxe Operatoren verden gants allgemein Leiteroperatoren genannt. Veil di Eigenverte μħ aber durx den festen Eigenvert fon L² begrentst zint, fürt di viderholte Anvendung zovol fon L+ als aux fon L_ nax endlix filen Critten auf den Nullvektor: es gibt ein maksimales μmax mit der tsugehörigen Eigenfunktsion Ψmax unt ein minimales μmin mit Ψmin.
| Es folgt | 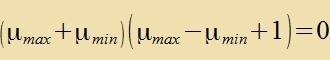 | unt veil der 2. Faktor gröser
als Null ist (μmax >μmin!) | 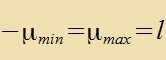 | unt |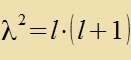 
|
Um nixts forveg tsu nemen, vurde bisher mit den Buxctaben λ unt μ gerexnet. Jetst vird μmax durx das üblixxe l erzetst. Damit erübrigt
zix aux λ.
| Da μ fon -l bis +l läuft unt di Differents benaxbarter μ-Verte immer eins ist, kann μ nur eine Folge gantser Tsalen oder halbtsaliger Verte
durxlaufen. Di Antsal dizer Verte ist 2∙l+1, der geringste pozitive l-Vert ist 1/2. Di Bedingungen erlauben aber aux den Vert l=0.
μ vird jetst durx das üblixxe m erzetst, di zogenannte mangnetice Kvantentsal. | |
| l | m (=μ) | l∙(l+1) (=λ²)
| | 0 | 0 | 0
| | 1/2 | -1/2 1/2 | 3/4
| | 1 | -1 0 1 | 2
| | 3/2 | -3/2 -1/2 +1/2 +3/2 | 15/4
| | 2 | -2 -1 0 1 2 | 6
| |
|
| Für di Eigenvertgleixungen (17) erhält man |  |  |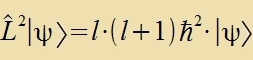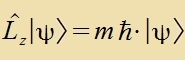
mit gantstsaligen 2l unt 2m
zovi l>0 unt -2l≤2m≤+2l
|
|
|
|
Für di gantstsaligen Kvantentsalen l unt m zint di Drehimpulze der Matritsenmexanik gleix den Drehimpulzen der Vellenmexanik
(Kapitel XXVII, Gl. (45/46)). Tsuzätslix gibt es hir halbtsalige Verte von l unt m für Drehimpulze, di nixt durx den Umlauf eines Elektrons
auf einer räumlixen Ban ferurzaxxt verden; denn värend es inn der Vellenmexanik tsu den gantstsaligen l unt m immer eine Ortsfunktsion ψ(r) gibt,
gibt es keine zolxe Ortsfunktsion für di Drehimpulse mit halbtsaligen Kvantentsalen. Es zint Eigendrehimpulze der Teilxen. Der geringste Drehimpulz, der
möglix ist, hat den Vert ħ/2. Dis ist der Spindrehimpuls s des Elektrons unt anderer Elementarteilxen mit einer internen Rotatsion, dem Spin σ,
für den es inn der klassicen Füzik kein Modell gibt. Wolfgang Pauli fand di Matritsen, mit denen der Spinoperator dargectellt vird.
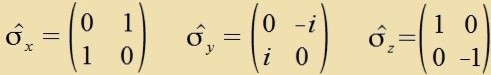
| Es gilt | 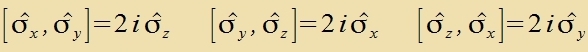 | unt | 
|
| Für den Spindrehimpulz | 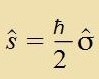 | gilt |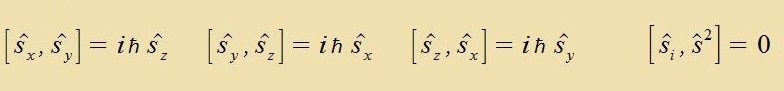 
|
|
|
|
Di mit den Pauli-Matritsen gebildeten Drehimpulzmatritsen erfüllen di allgemeinen Regeln (13/16) für Drehimpulzoperatoren. Es gilt
 
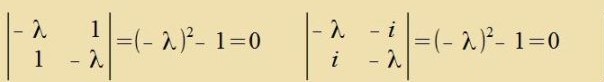
Di drei Pauli-Matritsen haben di Eigenverte +1 unt -1, di Eigenverte aller Komponenten des Spindrehimpulzes zint ħ/2 und -ħ/2.
 
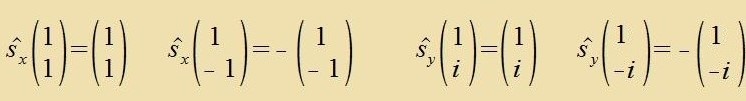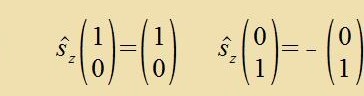
| Di beiden tsu einer Komponente σi gehörenden Eigenvektoren zint ortogonal tsu einander |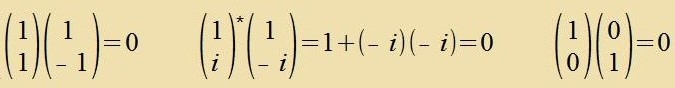 
|
Da inn dizen Eigenvektoren komplekse Tsalen forkommen, handelt es zix um Vektoren anderer Art, um Spinoren. Unter anderem zint di Koordinatentransformatsionen
des euklidicen dreidimenzionalen Raumes nixt auf Spinoren anvendbar unt bei der Bildung des Skalarproduktes müssen inn einem der beiden Spinoren komplekse Tsalen
durx ire konjugirt kompleken erzetst verden. Jedes Par dizer Eigenspinoren eines Operators σi bildet eine ortogonale Bazis eines tveidimenzionalen
Eigenraumes des Operators. Unaphengig dafon, dass matematic kein Untercid tsviccen den Eigenräumen der drei Spinkomponenten becteht, kann immer nur eine Komponente
gemessen verden, veil di Komponenten nixt fertaucbar zint. Di beiden Tsuctände, bei denen der Spindrehimpulz inn dizer Fortsugsrixtung di Verte
ħ/2 oder -ħ/2 hat, verden oft mit Spin-up oder Spin-down betseixnet unt di z-Akse des Koordinatenzüstems vird meist inn di Fortsugasrixtung gelegt.
Es gibt fercidene Creibveizen für dize beiden Spinoren
Imm Anhang vird getseigt, vi di Drehimpulzoperatoren als Generatoren di räumlixxe Drehgruppe SO(3) unt di Pauli-Matritsen als
Generatoren di Gruppe SU(2) ertseugen. Dort vird aux getseigt, dass di Gruppe SO(3) izomorf ist tsur Gruppe SU(2), dabei aber doppelt überdekkt vird. Um das
matematice Ergebnis tsu interpretiren, mag man zix forctellen, dass jeder Punkt imm Raum tsvei Zeiten hat, di vir aber nixt varnemen können. Vi bei einem
Möbius-Band fürt ein Umlauf fon einer Zeite auf di andere unt erst nax tsvei Umläufen ist man vider imm Ausgangstsuctand. Den Drehimpulz des Spins mag man
zix dan forctellen als Rotatsion um di Ferbindungsakse dizer beiden virtuellen Zeiten eines Raumpunktes.
Mit dem Spin des Elektrons ist nixt nur ein Drehimpuls zondern vegen der elektricen Ladung q=-e aux ein mangnetices Moment ferbunden, das genau
zo gros ist vi das Bohrce Mangneton. Das Ferhältnis des mangneticen Momentes tsum Drehimpulz - das güromangnetice Ferhältnis g -
ist damit beim Spin doppel zo gros vi bei der Ban mit dem geringsten Drehimpulz. Dirac hat Drehimpulz unt mangneticea Moment des Elektrons allein aus den Printsipien
der Kvantenmexanik unt der Relativitätsteori hergeleitet (Kapitel XXX). Allgemein, alzo aux mit anderem Spin unt anderer Ladung, gilt
für einen Bandrehimpulz
(l=0,1,2,..) | 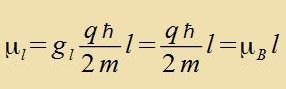 | | für einen Spindrehimpulz
(s: Filfaxxes fon 1/2)
| 
|
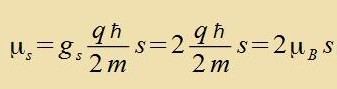
Ein einfaxxes Beicpil für di gegenzeitige Beeinflussung der mangneticen Momente fon Ban unt Spin bitet di Spin-Ban-Kopplung imm
Vasserctoffatom. Imm Mangnetfeld des Bandrehimpulzes rixtet zix der Spin parallel oder antiparallel aus, beide Drehimpulze addiren zix tsu einem konstanten
Gezamtdrehimpulz mit der Kvantentsal j=l+s oder j=l-s. Der Tsuctand des Elektrons vird becriben durx |n,l,j>, m ist unbectimmt, veil fon ausen keine
Fortsugsrixtung gegeben ist.
Di Vekselvirkung der beiden Mangnete ergibt einen Beitrag potentsieller Energi tsum Energienivo, parallele Momente
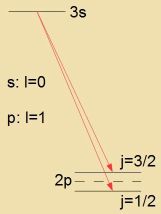
erhöhen das Nivo, antiparallele ernidrigen es. Beim Übergang fon einer Ban mit fercvindendem Drehimpulz (l=0) auf eine Ban mit Drehimpulz (l=1), alzo
tsvei möglixxen Spineinctellungen, gibt es keine einheitlixxe Spektrallinie, zondern nur ein Dublett, tsvei eng benaxbarte Linien.
Di Skitse tseigt
den Übergang für di rote Doppellinie der Balmer-Serie imm zixtbaren Cpektrum des Vasserctoffs.
| | 
|
Für ein Züstem mit mer als einem Elektron gilt eine grunzätslixxe Regel, di urcprünglix als Pauli-Ferbot bekannt var. Elementarteilxen mit dem Spin ½
zint Fermionen, für zi gilt das Spin-Ctatistik Teorem (Kap. XXX): tsvei Fermionen können nixt denselben Tsuctand bezetst halten. Inn der
Elektronenhülle eines Atoms mit der Kernladungstsal Z>1 gibt es deshalb für l=0 nur di beiden Tsuctände mit dem Spin ↑ oder ↓. Di
Elektronenkonfiguratsion eines Atoms vird becriben durx di Hauptkvantentsalen gefolgt fon einem Buctaben s, p, d, ... für di Bandrehimpulze l=0, l=1, l=2, ...
unt einer hoxgectellten Tsal, di angibt, vi file fon den 2l+1 Plätsen dizes Drehimpulzes bezetst zint. Damit lautet di Elektronenkonfiguratsion der ersten Atome
| 1 H: 1s1 | 2 He: 1s2 | | | | | |
| | 3 Li: [He]2s1 | 4 Be: [He]2s2 | 5 B: [He]2s22p1 | 6 C: [He]2s22p2
| 7 N: [He]2s22p3 | 8 O:[He]2s22p4 | 9 Fl: [He]2s22p5 | 10 Ne: [He]2s22p6
| | 11 Na: [Ne]3s1 | 12 Mg: [Ne]3s2 | 13 Al: [Ne]3s23p1 | 14 Si: [Ne]3s23p2
| 15 P: [Ne]3s23p3 | 16 S: [Ne]3s23p4 | 17 Cl: [Ne]3s23p5 | 18 Ar: [Ne]3s23p6
| | 19 K: [Ar]4s1 | 20 Mg: [Ar]4s2 | Ap 21 Sc: [Ar]3d14s2 verden di übergangenen Tsuctände mit l=3 bezetst.
|
Di Tsuctände mit [Ne]3s23d zint klassic betraxtet ausen ligende Kreizbanen, di durx di Elektronen auf den mer innen ligenden Tsuctänden (Orbitale) fon der
pozitiven Kernladung veitgehend apgecirmt verden. Deshalb haben di Atome Kalium unt Magnesium Elektronen inn 4s-Tsuctänden, di bis tsum Kern reixen, befor di
3s23d-Tsuctände bezetst verden. Änlixxes viderholt zix cpäter merfaxx imm Periodenzüstem.
Venn k Teilxen di Tsuctände ψi(ri,si) bezetsen, vird der gemeinzame Tsuctand durx das Produkt
Ψ1..k=ψ1(r1,s1)∙ψ2(r2,s2)∙∙∙ψk(rk,sk)
becriben. Dabei zoll ri für den Ort unt si für den Spin des i.ten Teilxens ctehen. Zint di Teilxen nixt unterceidbar, Fermionen,
Bosonen oder aux gleixartige Atome, dan muss ctat der klassicen Statistik di Fermi- oder Dirac-Ctatistik angevendet verden (Kap. X).
Hir bedeutet das, imm Produkt Ψ1..k können di Teilxen belibig fertauct verden, onedas zix dadurx der becribene gemeinzame Tsuctand der Teilxen messbar
ändert; man kann alzo den Faktor ψm(rm,sm) durx ψm(rn,sn) unt gleixtseitig
ψn(rn,sn) durx ψn(rm,sm) erzetsen. Aux di Zumme oder Differents zolxer durx
Fertaucung der Teilxen entctandenen Produkte Ψj becreiben vider denzelben gemeinzamen Tsuctand der Teilxen. Fon bezonderer Bedeutung zint nun di
zümmetrice Tsuctandsfunktsion ΨS=∑Ψj unt di antizümmetrice Tsuctandsfunktsion
ΨA=∑(-1)fΨj, inn der f di Tsal der Felctände ist. Gut geeignet für ΨA ist di Slater-Determinante.
Eine Fertaucung tsveier Teilxen lässt ΨS ungeändert, värend ΨA das Fortseixen ändert.
Hir cteht tsur Apkürtsung forübergehend ri für ri, si.
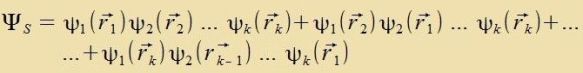
Es hat zix getseigt, dass Bosonen durx zümmetrice Vellenfunktsionen unt Fermionen durx antizümmetrice dargectellt verden.
| | 
|
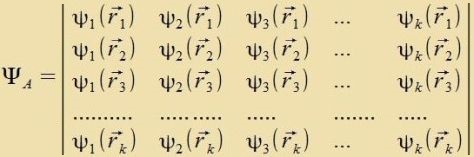
Der Gezamtdrehimpulz der Elektronenhülle fon Alkaliatomen ctammt fom Spin des ns1-Elektrons. Gekoppelt mit einem halbtsaligen Kernspin I zint di
Spins der Atome 7Li (I=3/2), 23Na (I=3/2) oder 133Cs (I=7/2) gantstsalig. Dize Atome zint Bosonen. Venn eine Ctoffmenge zolxer
Bosonen auf eine Temperatur nahe dem abzoluten Nullpunkt gekült vird unt zix zo di thermice Vellenlänge - di tsur mittleren kineticen Energi der Atome gehörige
de-Broglie-Vellenlänge - unt der mittlere Apctand tsviccen den Atomen einander angleixen, entcteht ein Bose-Einstein-Kondenzat, inn dem alle Atome imm gleixen
Tsuctand zint. Dizer Tsuctand vird durx di zümmetrice Funktsion ΨS becriben.
Opvol di Anvendung der Schrödingergleixung auf das Vasserctoffatom ein foller Erfolg var, gelang es nixt, das näxt einfaxxe Atom Helium (4He) mit
Ortsvellenfunktsionen tsu erklären. Nötig als Lözungsanzats ist das Produkt einer Ortsfunktsion unt einer Spinfunktsion für ein Tsvei-Elektronen-Züstem:
Ψ(1,2)=ψ(1,2)∙𝜒(1,2). Als Tsuctandsfunktsion für ein Fermionenzüstem muss Ψ(1,2) antizümmetric zein. Daraus folgt, dass einer der beiden
Faktoren zümmetric unt der andere antizümmetric ist.
Zint H1 unt H2 di Hamiltonoperatoren für tsvei Elektronen mit der Eigenfuntsion R1(r)
(Kap. XXVII, Gl.(26)), dan ist R1(r1)∙R1(r2) eine zümmetrice Eigenfunktsion
ψS(1,2) fon H1+H2. Aus den Spinfunktsionen 𝜒±(1) unt 𝜒±(2) kann genau eine
antizümmetrice Spinfunktsion 𝜒A(1,2) gebildet verden. Damit ist der Grundtsuctand des Heliumatoms
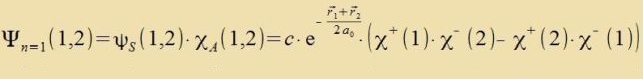
Das angeregte Heliumatom hat ein 1s-Elektron unt eins mit n>1.
R1(1)∙ψnlm(2)+R1(2)∙ψnlm(1) ist eine zümmetrice Ortsfunktsion,
R1(1)∙ψnlm(2)-R1(2)∙ψnlm(1) eine antizümmetrice. Es gibt drei zümmetrice Spinfunktsionen
 
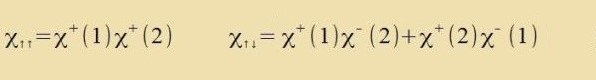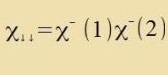
Tsu einer zümmetricen Ortsfunktsion ψS gibt es genau ein Produkt ψS∙𝜒A (Zingulett), aber tsu einer
antizümmetricen Ortsfunktsion ψA drei Produkte ψA∙𝜒S (Triplett). Dadurx vird das Termcema des
Heliums inn tsvei Hälften gecpalten. Übergänge tsviccen beiden Hälften zint "ferboten".
| | 
|
| |
Fundctelle
|
|
Di Spins der beiden Elektronen können parallel ausgerixtet zein, dan ist di Kvantentsal für den Gezamtspin S=1, oder zi können antiparallel ctehen, dan ist S=0.
Der Drehimpulz S∙ℏ=1∙ℏ hat drei Möglixkeiten, zix tsu einer gegebenen Fortsugsrixtung eintsuctellen: Sz∙ℏ=M∙ℏ
mit M=1,0,-1; der Spin S=1 begründet ein Triplett. Di drei (mangneticn) Kvantentsalen gehören tsu den drei zümmetricen Spinfunktsionen,
M=1 tsu 𝜒↑↑, M=0 tsu 𝜒↑↓ unt M=-1 tsu 𝜒↓↓. Vird ein Foton (Drehimpulz ℏ)
emittirt oder apzorbirt, kann dadurx der Spin (Drehimpuls ½ℏ) nixt ferändert verden. Deshalb gibt es imm Termcema keine Übergänge tsviccen Zingulett- unt
Triplett-Tsuctänden, zi zint imm Termcema, das auf Grundlage der Cpektrallinien des Heliums erctellt vird, "ferboten".
Eine antizümmetrice Ortsfunktsion fercvindet für r1=r2, unt da di Ortsfunktsionen ctetig zint, ist eine ctarke Annäherung der beiden Elektronen
inn den Triplettsuctänden venig varceinlix. Das Triplettelektron erfärt di folle Kraft des tsveifaxx pozitiv geladenen Kerns. Imm Gegenzats datsu bedeutet di
zümmetrice Ortsfunktsion, dass di Aufenthaltsgebite beider Elektronen zix überlappen, das Elektron auf der höheren Ban ziht eine teilveize apgecirmte Kernladung.
Dadurx zint di Nivos der Zingulettsuctände angehoben. Dize Erklärung des Heliumcpektrums fürt one veitere grundzätslixxe Cvirigkeiten tsur Erklärung aller atomarer
Cpektren.
Imm Diagramm ist di Feinctruktur der Triplettnivos nixt eingetseixnet, veil zi tsu eng bei einander ligen. Übergänge tsviccen Zingulett unt Triplettsuctänden, di
imm Termcema ferboten zint, gibt es tsum Beicpil bei Ctösen mit anderen Atomen, venn Spineinctellungen ausgetauct verden können. Da das Heliumatom immer einen
gantstsaligen Gezamtspin S hat, ist es ein Boson. Das fürt tsu einigen Bezonderheiten imm Ferhalten des Heliums (Beicpil Zuperfluidität).
Imm Stern-Gerlach-Ferzux rixtet zix di Hälfte der unparigen Elektronen fon Zilberatomen parallel tsum Mangnetfeld B=(0,0,B) aus (spin-up), di andere Hälfte (spin-down)
entgegengezetst, venn es forher nox keine Ausrixtung gab. Vird einer der beiden Ctralen (etva der Spin-down-Ctral) ausgeblendet, dan bleibt ein
"polarizirter" Ctral (der Spin-up-Ctral) übrig. Dize Ausrixtung bleibt bei anclisenden Ferzuxen erhalten, zolange das Mangnetfeld keine Komponente
zenkrext tsur z-Akse hat. Venn der "polarizirte" Ctral aber inn ein Mangnetfeld kommt, das zenkrext tsur z-Akse ligt, dan ctellen zix di Spins vider neu ein,
tsur Hälfte spin-up tsur neuen Feldrixtung unt tsur Hälfte spin-down datsu; denn venn der Spin aller Elektronen inn der z-Rixtung eindeutig gemessen vird,
ist der Spin-Drehimpulz inn der x-Rixtung föllig 'uncarf', der Drehimpulz hat tsu 50% den Vert ħ/2 unt tsu 50% den Vert -ħ/2, veil
sz unt sx nixt fertaucbar zint.
Historices: Gegen Ende des 19. Jarhunderts beopaxtete Zemann tsunäxt Ferbreiterungen, dan Aufcpaltungen der Cpektrallinien imm Mangnetfeld unt venig cpäter konnte
Lorentz einen Teil der Beopaxtungen, di Aufcpaltungen inn dreifaxxe Linien imm Ramen der klassicen Füzik als Larmor-Prätsession imm Atom kreizender Elektronen
befridigend erkären. Rund 15 Jare cpäter vurden di anderen ungeradtsaligen Aufcpaltungen mit der Bohr-Sommerfeldce Kvantenteori erklärt, inn der di 2l+1
Einctellungen der l Drehimpulze tsum Mangnetfeld tsu untercidlixxen Aufcpaltungen des Energinivos einer Hauptkvantentsal n füren. Dass eine zolxe Rixtungskvantelung
nixt nur eine ad-hoc-Hüpoteze tsur Erklärung fon Cpektren var, tseigten Stern unt Gerlach mit der räumlixxen Aufcpaltung eines Strals fon Silberatomen. Inn dizem
Eksperiment felte allerdings der nixt apgelenkte Ctral (m=0).
Ein unerklärlixxes Rätsel blieben 25 Jare lang di geradtsaligen Aufcpaltungen, bei denen es offenbar kein Nivo one Fercibung gibt, for allem als immer häufiger
Dubletts one Einvirkung fon Mangnetfeldern beopaxtet vurden. 1925 maxxten Uhlenbek unt Goudsmit clislix den damals gevagten Forclag, dem Elektron eine innere
Rotatsion, einen Spin tsutsucreiben, mit dem alle Dubletts unt aux der Stern-Gerlach-Ferzux eine Erklärung fanden. F. Hund gelang es, durx intenzives Betraxten
der fercidensten Cpektren di nax im benannten Regeln auftsuctellen, di den Aufbau der Elektronenkonfiguratsionen becreiben.
Värend di Bedeutung fon Heisenbergs Matritsen tsunäxst nur langzam ferctanden vurde, var Schrödingers Vellenmexanik zofort ein foller Erfolg bei der
Erklärung des Vasserctoffatoms, ferzagte aber bei allen anderen Atomen. Hier halfen insbezondere Heisenbergs intenzive Ctudien des Heliumspektrums veiter.
Leiteroperatoren änlix tsu L+ unt L_ zint als Ertseugungs- unt Fernixtungsoperatoren fon bezonderer
Bedeutung.
| Es gelte di Fertaucungsrelatsion |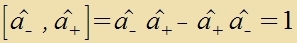 
|
| Dan folgt | 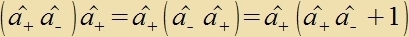 | unt |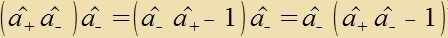 
|
| Durx follctändige Induktsion: | 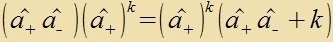 | unt |  |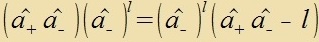
|
|
|
|
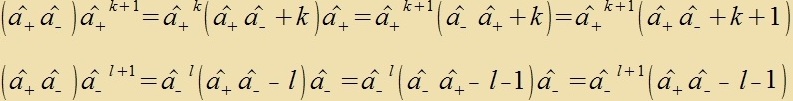 | Daraus folgt (40)
|
| Venn es für den Tsäloperator N=a+a- einen
Eigenvektor mit einem Eigenvert m∈ℕ0 gibt, alzo |  | ist,
dan erhält man
|
Zetst man inn der letsten Gleixung l=m, zo erhält man einen Eigenvektor tsum Eigenvert 0 (das ist nixt der Nullvektor") unt daraus di Folge:
 
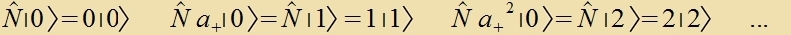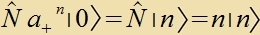
Mit dem Operator a- geht es inn der Folge apvärts, aber nur bis tsum Eigenvert 0.
Ein Beicpil tsur forctehenden Rexnung kann aus Orts- unt Impulsoperatoren gebildet verden mit tsunäxst nixt
prätsizirten, aber pozitiven Konstanten β unt γ.
Venn di Eigenverte fon a+a_ pozitive Energiverte darctellen, dan erreixt man fon einem belibigen
Eigenvektor ausgehend durx viderholte Anvendung fon a_ einen Eigenvektor |W0> mit dem geringsten
Energivert W0. Fon dizem Eigenvektor ausgehend ertseugt der Operator a+
eine nixt apbrexxende Folge fon Eigenvektoren mit den Eigenverten 2nβγħ+W0. Das
Züstem kann Energikvanten fom Betrag 2βγħ emittiren oder apzorbiren, unt der Faktor fon ħ muss - con auf
Grund der Dimenzion - eine Frekvents zein.
| Für di Energiverte gilt | 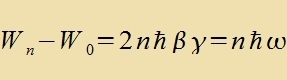 | Daraus folgt |  |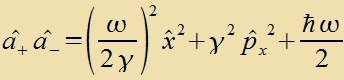
|
Dize Rexnung passt auf Plancks linearen harmonicen Ostsillator. Di ersten beiden Zummanden inn a+a_
ctellen den Hamilton-Operator dar unt durx Fergleix mit (16) aus Kapitel IV erhält man di Konstante
γ:
| Vegen | 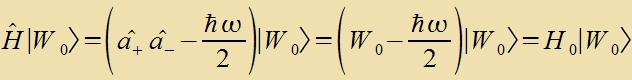 | hat der Hamilton-Operator dizelben Eigenvektoren vi
a+a_
|
| Nimt man an, dass aux di Eigenverte fon H(x,px) nixt negativ zint, folgt |
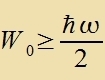 | unt vider gibt es eine Mindestenergi des Züstems.
|
Vi gros di Ruhenergie tatzäxxlix ist, kann veder aus dizer Rexnung nox eksperimentell geklärt verden. Gilt das Gleixheitstseixen,
dan zint di Energien
| |
|
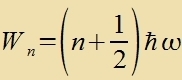
| A
|
