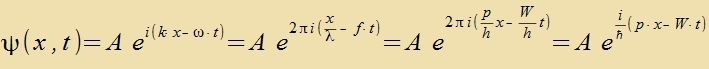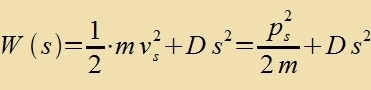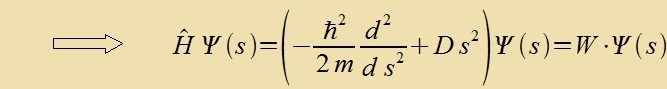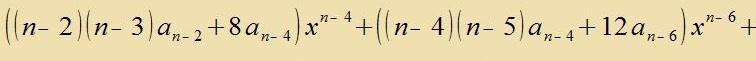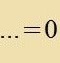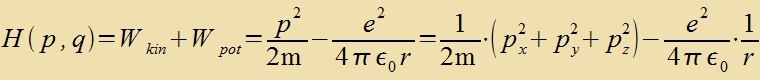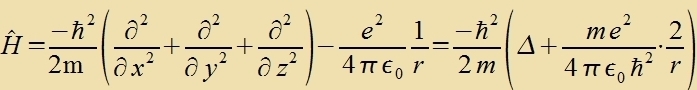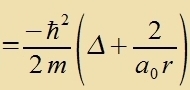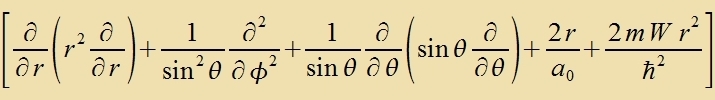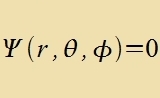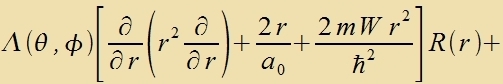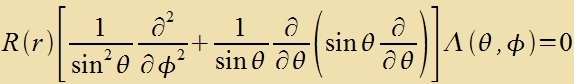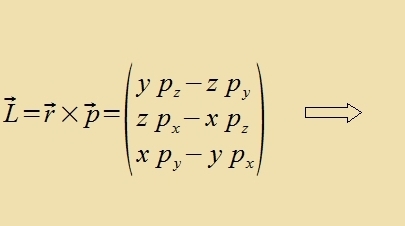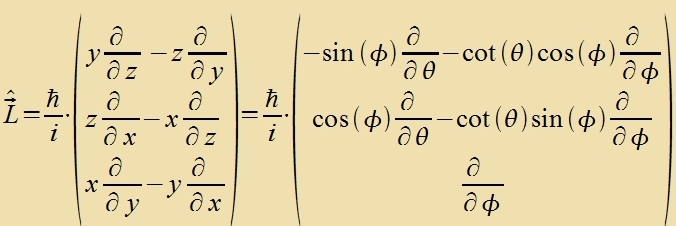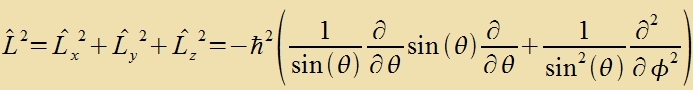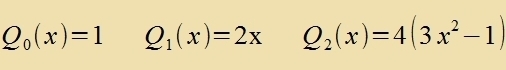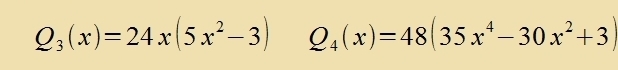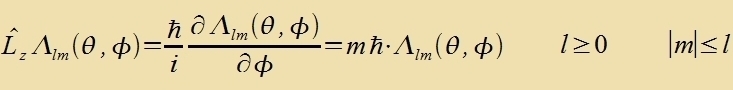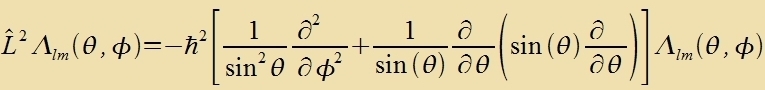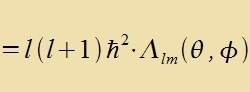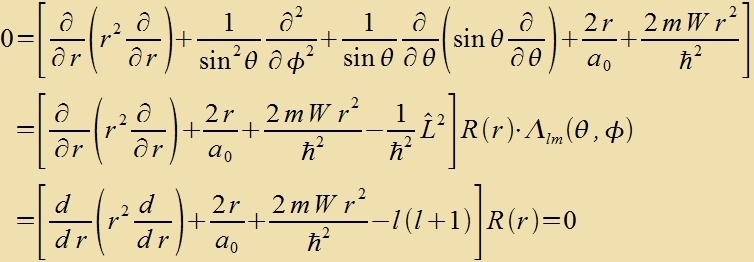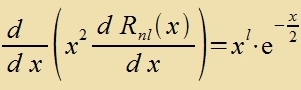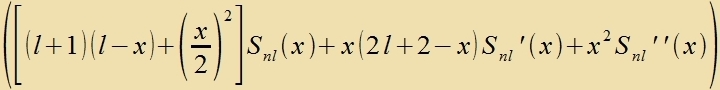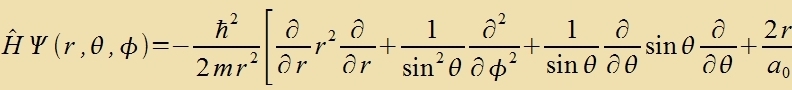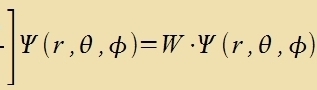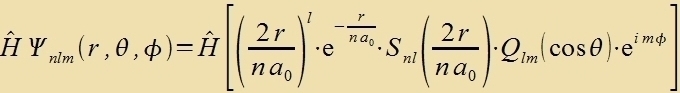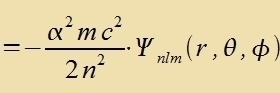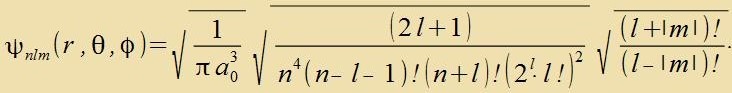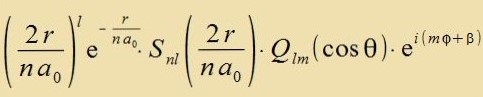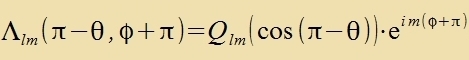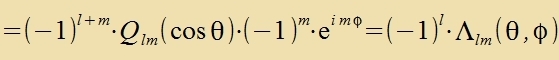Füzik

Home

XXVII. Vellenmexanik

Porträ (bearbeitet) Fundctelle Schrödinger

	Tsu einem freien Elektron, das zix geradlinig mit dem Impulz p=(px,0,0)=(p,0,0) bevegt, gehört eine ebene Velle ψ(x,t), di das Interferentsmuster am Doppelcpalt ertseugt. Ire Frekvents ist f=W/h (Planck, Gl. (2) inn Kap. XXV) unt ire Vellenlänge λ=h/p (de Broglie, Gl. (1) inn Kap. XXVI).	(1)
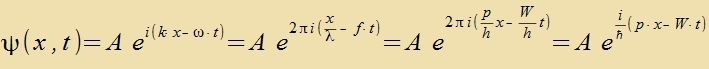
	Mit der kompleksen Creibveize verden vi üblix tsvei linear unaphengige Funktsionen als Realteil unt Imaginärteil tsuzammengefasst. Dize Vellengleixung vird einerzeits nax der Tseit unt andererzeits einfaxx unt doppelt nax der Ortskoordinate x differentsirt.	(2)
	Unt vegen 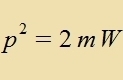folgt di Schrödingergleixung für das freie Teilxen	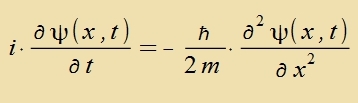(3)
	Di Betsihungen tsviccen füzikalicen Grösen verden inn der klassicen Füzik durx algebraice Gleixungen becriben. Unbekannte Grösen eines Züstems können berexnet verden, venn genügend Gleixungen unt genügend bekannte (gemessene oder angenommene) Grösen forligen. Inn dizem Zinne kann aux di Relativitätsteori tsur klassicen Füzik gerexnet verden. Tsu Anfang des 20. Jarhunderts tseigte zix aber, dass zolxe Ferfaren nixt mer angebraxt zint, venn Erceinungen imm Grösenbereix der Atome behandelt verden. Dort müssen di matematicen Ferfaren darauf gerixtet zein, nixt nur kontinuirlixer Verte für füzikalicen Grösen tsu lifern zondern for allem aux diskrete Verte. Für das freie Teilxen ertseugt di obige Schrödingergleixung tsvar aux nur kontinuirlixxe Verte, tseigt aber dox einen Veg tsur Lözung des angecproxxenen Problems: Gezuxt zint Funktsionen, di bis auf einen konstanten Faktor übereinctimmen mit bectimmten Apleitungen irer zelpst. Es handelt zix um Eigenvertgleixungen, di Lözungsfunktsionen zint di Eigenfunktsionen, di konstanten Faktoren zint di tsugehörigen Eigenverte. Eigenverte können je nax den Umctänden diskret zein oder kontinuirlix vi beim freien Teilxen. Di Differentsialoperatoren tsuzammen mit dem Faktor h/2πi zint di Operatoren derjenigen füzikalicen Grösen, tsu denen di jeveiligen Eigenverte gehören. Operatoren verden mit einem Daxx über dem Zymbol der füzikalicen Gröse gekenntseixnet. Der Impulzoperator, der bisher der Einfaxxheit halber nur für di x-Rixtung begründet vurde, gilt entcprexxend inn allen drei Raumrixtungen. Aus den Gleixungen (2) folgt	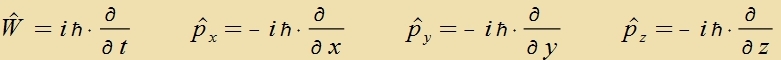(4)
	Es gilt 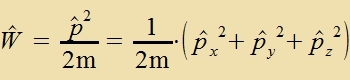Das ist di gleixe Betsihung tsviccen Energi unt Impulz vi inn der klassicen Füzik. Bei konstanter Energi kann Gl. (1) gecriben verden als 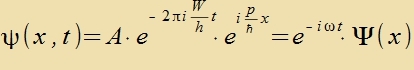Ψ(x) ist ein ctatsionärer Tsuctand. Tseigt ein Züstem diskrete Energiverte, dan gibt es tsu jedem Wn eine Funktsion Ψn(x), allgemeiner Ψn(q), vobei q für belibige dreidimenzionale Ortskoordinaten cteht. Der Tsuctand, den dize Ortsdarctellung Ψn(q) darctellt, vird als ctehende Velle interpretirt, unt di Eigenverte des Energioperators angevendet auf Ψ(q) zint di möglixxen Energiverte. 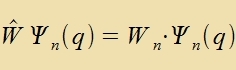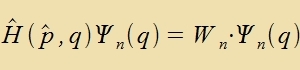Venn inn der klassicen Füzik di Energi nixt fon der Tseit aphengt unt allein durx di Impulz- unt Ortskoordinaten ausgedrükkt verden kann, vird zi als Hamiltonfunktsion gecriben. Inn di Kvantenmexanik übertragen müssen dan di Impulskoordinaten durx di entcprexxenden Operatoren nax Gleixung (4) erzetst verden. Als ein erstes Beicpil vird der lineare harmonice Ostsillator behandelt. Ausgangspunkt ist di Gleixung für di Energi der Federcvingung (Kapitel IV, Gl. (16)). 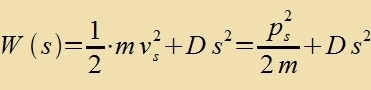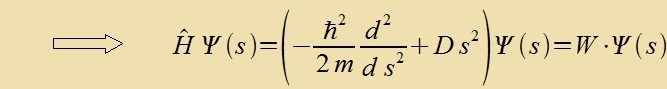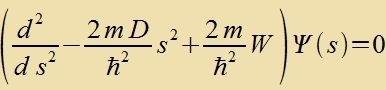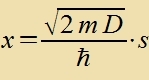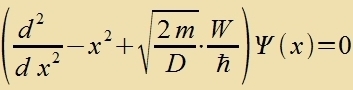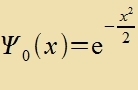Di Zupstitutsion fürt tsu	(7)  (8)
	ist eine Lözung der Differentsialgleixung (8c), unt der tsugehörige Eigenvert für di Energi ist 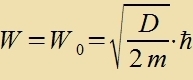Um veitere Lözungen der Differentsialgleixungen tsu finden, vird Ψ0(x) als Faktor beibehalten unt durx Polünome Un(x)=anxn+an-1xn-1+...+a1x+a0 'modulirt'. Zetst man 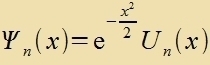unt 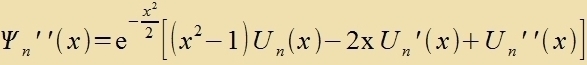inn Gleixung (8c) ein, dan erhält man di Differentsialgleixung 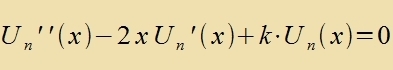mit 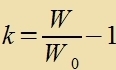unt für di Koeffitsienten fon Un(x)	(11) (12)
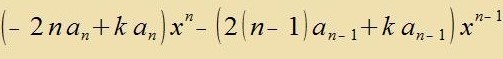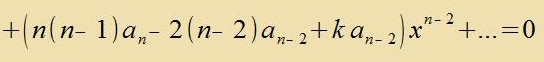
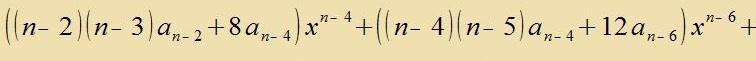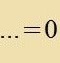
	Hir müssen di Faktoren for jeder Potents fon x fercvinden. Daraus folgt Aus der Differentsialgleixung (11) ist erkennbar, dass inn den Faktoren aller Potentsen fon x imm Nullpolünom (12) immer nur tsvei Koeffitsienten ai forkommen, deren Inditses zix um 2 unterceiden. Aus an-1=0 folgt deshalb an-3=an-5=an-7=...=0. Fom Nullpolünom (12) bleibt Di Koeffitsienten an haben di Rekurzionsformel 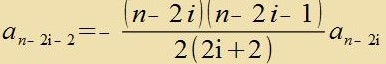Mit 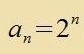zint di ersten fünf hermitecen Polünome 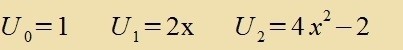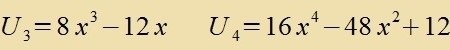Un(x) lözt di Differentsialgleixung (11) mit k=2n, Ψn(x) lözt di Differentsialgleixung (8) mit Wn=(k+1)W0 =(2n+1)W0 unt Ψn(s) lözt di Differentsialgleixung (7). Gleixung (7) ist eine Eigenvertgleixung: Di Virkung des Differentsialoperators auf di Funktsion Ψn(s) becteht allein darin, dass di Funktsion Ψn(s) mit dem konstanten Vert Wn einer Obzervablen multiplitsirt vird. Ψn(s) ist eine Eigenfunktsion des Differentsialoperators tsum Eigenvert Wn. Der Differentsialoperator ist ein Hamiltonoperator, er ist aus der Energi des Züstems hergeleitet unt hat Energiverte als Eigenverte. Ψn(s) becreibt einen möglixxen Tsuctand des linearen harmonicen Ostsillators mit dem möglixxen Energivert Wn. Beim Übergang tsviccen tsvei benaxbarten Tsuctänden vird di Differents ΔW=Wn+1-Wn=2W0 emittirt oder apzorbirt. Das ist Plancks Energiquant ℏω. Di Energiverte der möglixxen Tsuctände des Ostsillators zint Wn=(n+½)ℏω. Bemerkensvert ist insbezondere, dass es keinen Tsuctand gibt, inn dem der Ostsillator di Energi Null hätte, er hat immer mindestens di Nullpunktsenergi ½ℏω. Für n≠m gilt 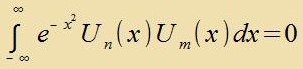Mit geeigneter Normirung bilden di hermitecen Polünome betsüglix der Gevixtsfunktsion exp(-x2) di ortonormale Bazis eines Hilbertraumes. Alle integrirbaren Funktionen können als unendlixxe Reihen mit dizen Polünomen entvikkelt verden. Für di hermitecen Polünome gibt es folgende Rodriguez-Formel. 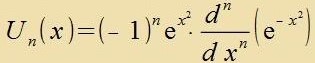zint di Lözungen der Differentsialgleixung (11) mit 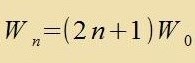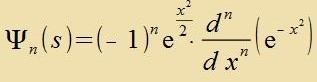zint di Eigenfunktsionen des harmonicen Ostsillators mit den Eigenverten 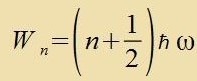Di klassice Hamilton-Funktsion für ein Elektron imm radialzümmetricen Tsentralfeld des Vasserctoffkerns becreibt di tseitunaphengige Energi des Elektrons als Funktsion der kanonic konjugirten Variablen Ort unt Impulz. 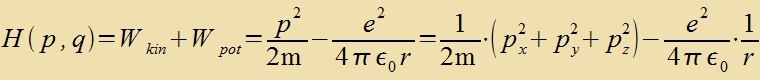Zi lautet Mit Gleixung (2) vird der Impulz durx den Impulzoperator erzetst, um zo den Hamilton-Operator für di Ortsdarctellung tsu gevinnen. 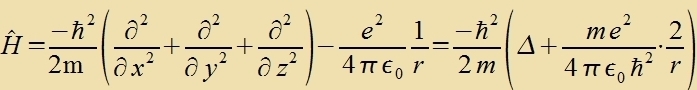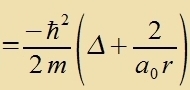Mit dizem Operator, inn dem tsur Apkürtsung der Bohrce Radius a0 (Gl. (3) Kapitel XXVI) eingezetst ist, erhält man di folgende Eigenvertgleixung 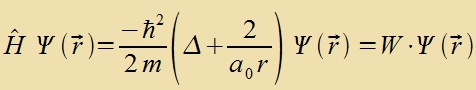unt	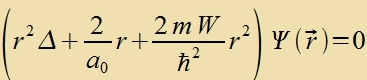(22)
	Der Laplace-Operator Δ ist einerzeits unaphengig fom Koordinatenzüstem, muss aber andererzeits entcprexxend tsur Zümmetri des Problems inn ein geeignetes Koordinatenzüstem umgerexnet verden. Das tsentralzümmetrice Feld des Vasserctoffkerns erfordert sfärice Koordinaten (r,φ,θ). Zetst man den umgerexneten Laplace-Operator ein, dan encteht di Schrödersche Vellengleixung für di möglixxen Energiverte des Elektrons imm Vasserctoffatom.	(23)
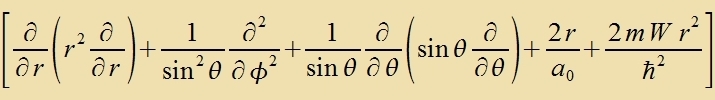
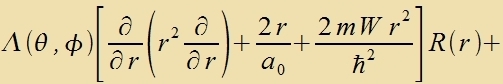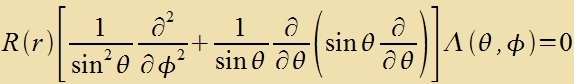
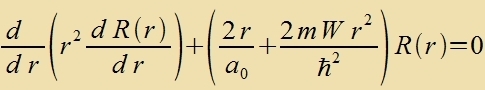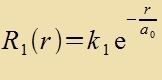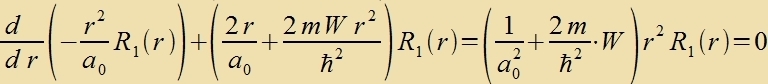
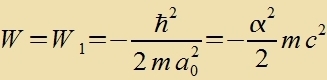
	Der Operator tserfällt inn tsvei Zummanden, fon denen einer nur auf Funktsionen fon r virkt unt der andere nur auf Funktsionen fon θ unt φ. Zetst man Λ(θ,φ)=1, zo bleibt eine Differentsialgleixung übrig, deren Lözungen radialzümmetric zint. Dize Gleixung bectimmt di Eigenverte W der Energi des Vasserctoffatoms. Der Anzats fürt tsu	(25) (26)
	ist der Eigenvert des Hamiltonoperators tsur radialzümmetricen Eigenfunktsion R1(r) Dizer Eigenvert der Energi ist derzelbe vi di Energi auf der ersten Bohrcen Ban. Es ligt daher nahe, bei der Zuxe nax veiteren Eigenfunktsionen di Bohrcen Energiverte tsugrunde tsu legen unt für W inn Gleixung (25) eintsuzetsen. Dadurx entcteht für jedes n eine Gleixung für eine Eigenfunktsion Rn(r). 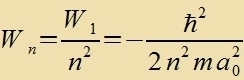Mit Gleixung (6) imm Kapitel XXVI Mit folgt Der Faktor 2 inn der Zupstitutsion ist tsvekkmäsig, um an di üblixxe Darctellung der Polünome antsuclisen, er vird inn der Eksponentsialfunktsion vider aufgehoben. Vi con bei der Behandlung des harmonicen Ostsillators vird di Funktsion R1(x) als Faktor beibehalten unt durx Polünome Pn(x) modulirt. Der Anzats 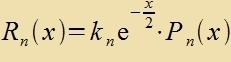fürt tsur Differentsialgleixung	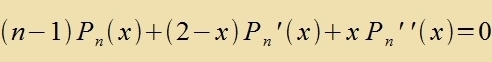(28) (29)
	Unmittelbar erkennbar zint di ersten beiden Lözungen 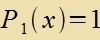unt 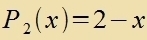P1 viderholt das oben con berexnete Ergebnis. Di näxsten tsvei Lözungspolünome zint 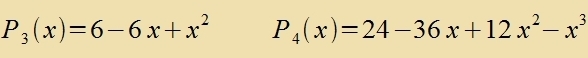Di Lözungen fon (29) zint di Laguerre-Polünome. Zi verden ebenfalls durx eine Rodriguez-Formel dargectellt.	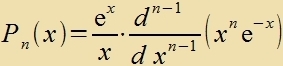(31)
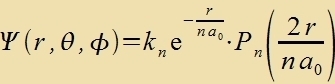
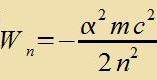
	Ergebnis: Di radialzümmetricen Funktionen zint Eigenfunktsionen der Schrödingercen Vellengleixung (25) mit den Eigenverten Di ersten fir zint nebenctehend dargectellt. Di kn zint geeignet gevält (one Begründung).	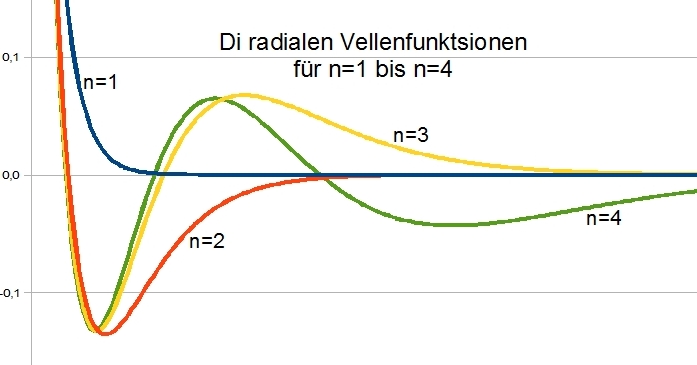(32) (33)
	Anders als imm Bohrcen Modell gibt es inn der Wellenmexanik Elektronenbanen, di am Ort des Atomkerns nixt fercvinden unt di keinen Drehimpulz haben. Für n≠m gilt 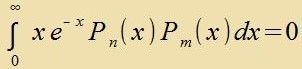Mit geeigneter Normirung bilden di Laguerre-Polünome betsüglix der Gevixtsfunktsion x∙e-x di ortonormale Bazis eines Hilbertraumes. Alle inn [0,∞] integrirbaren Funktionen können als unendlixxe Reihen mit dizen Polünomen entvikkelt verden. (31) ist di entcprexxende Rodriguez-Formel der Laguerre Polünome. Di radialen Vellenfunktsionen (32) können keine Verte für einen Drehimpulz beinhalten. Um zolxe Verte tsu finden, müssen di Vellenfunktsionen für den follctändigen Hamilton-Operator (23) aufgectellt verden. Forher verden hir di möglixxen Eigenfunktsionen unt Eigenverte des Bandrehimpulzes eines Teilxens allgemein unt unaphängig fom Vasserctoffatom unterzuxt. Ausgehend fom klassicen Drehimpulz erhält man den Bandrehimpulz-Operator, indem man di Impulzkomponenten entcprexxend tsur Gleixung (4b) erzetst. 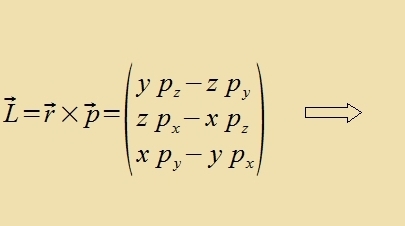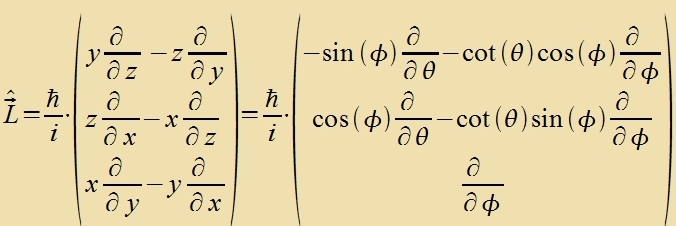Durx den Übergang tsu sfäricen Koordinaten vird di Rixtung θ=0 (z-Akse) tsur Fortsugsrixtung. Imm Eksperiment vird eine zolxe Fortsugsrixtung tsum Beicpil durx ein Mangnetfeld gegeben. Värend di Drehimpulzkomponente inn der Fortsugsrixtung tsu einer einfaxxen Eigenvertgleixung fürt, gibt es nixts dergleixen für di beiden anderen Komponenten. Für Lz zint di Eigenvertgleixung unt ire Lözung 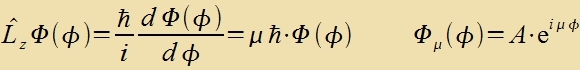mit reellem μ. Auser für di Komponente inn der Fortsugsrixtung gibt es für di Gröse des Drehimpulzes (imm Kvadrat) Eigenverte unt Eigenfunktsionen. Der Differentsialoperator für di Gröse des Drehimpulzes ist inn sfäricen Koordinaten	(35) (36)
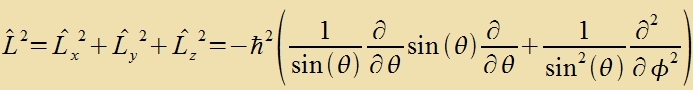
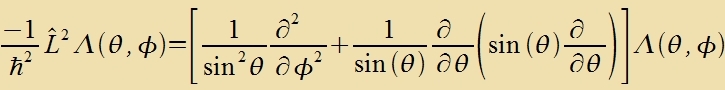
	Dizer Operator ist ein Teil des Hamilton-Operators (23) für das Elektron imm Vasserctoffatom. Mit dem Anzats Λ(θ,φ)=1 ferkürtste zix Gleixung (23) tsur Gleixung (29) mit den radialzümmetricen Vellenfunktsionen als Lözungen, deren Drehimpulz fercvindet. Di Eigenvertgleixung für L2 lautet Hir kann Λ(θ,φ) = Θ(θ)⋅Φ(φ) gezetst verden, veil di Apleitungen nax θ unt φ inn fercidene Zummanden getrennt zint. Mit (35) erhält man 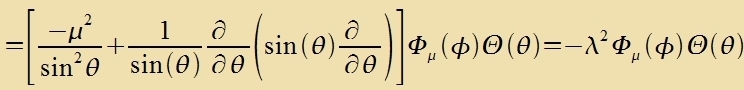Eigenvertgleixung für L² Jetst kann durx Φμ dividirt verden. 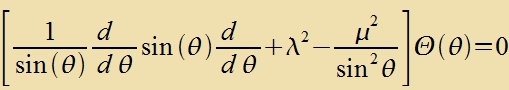Es ist üblix, hir cos θ tsu zubstituiren.	(37) (38) (39) (40)
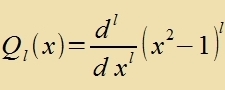
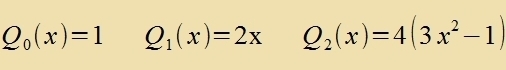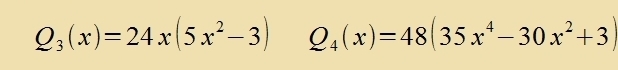
	Dize Differentsialgleixung ist nax Legendre benannt. Für μ=0 hat zi genau dann ctetige Lözungen imm Definitsionsbereix der cos-Funktsion, venn λ²=l(l+1) ist mit gantstsaligen, nixt negativen Verten fon l. Di Lözungen zint di Legendre-Polünome, di vider durx eine Rodriguez-Formel gegeben zint.	(41)
	Für n≠m gilt 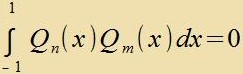Mit geeigneter Normirung bilden di Legendre-Polünome di ortonormale Bazis eines Hilbertraumes. Alle imm Intervall [-1,+1] integrirbaren Funktionen können als unendlixxe Reihen mit dizen Polünomen entvikkelt verden. (41) ist di tsugehörige Rodriguez-Formel. Ist μ nixt gleix 0 inn Gleixung (40), dan erhält man ortogonale Polünome als Lözungen nur für gantstsalige Verte fon μ, di fon -l bis +l gehen. Dis zint di 'mangneticen' Kvantentsalen m. Di Lözungen fon Gleixung (40) für μ=m zint di assotsiirten Legendre-Polünome Qlm(x) mit der Rodigruez-Formel 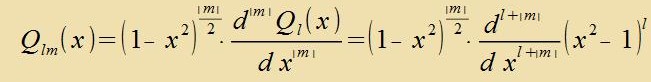mit	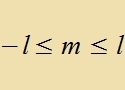(43)
	Als Beicpil vird imm Anhang konkret naxgerechnet, dass das assotsiirte Legendre-Polünom Q4;-3(x) eine Lözung fon Gleixung (40) ist. Nimt man imm Ergebnis di Zupstitutsion tsurük unt erzetst x vider durx cosθ, zo erhält man di folgenden Funktsionen Qlm(cosθ) Di Kugelfläxxenfunktsionen zint	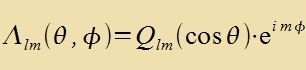(44)
	Mit den gantsen Tsalen l und m erfüllen di Kugelfläxxenfunktsionen di Eigenvertgleixungen für den Drehimpulz unt zeine Komponente inn der Fortsugsrixtung.	(45) (46)
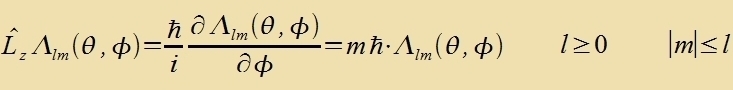
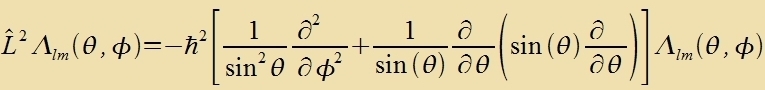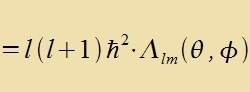
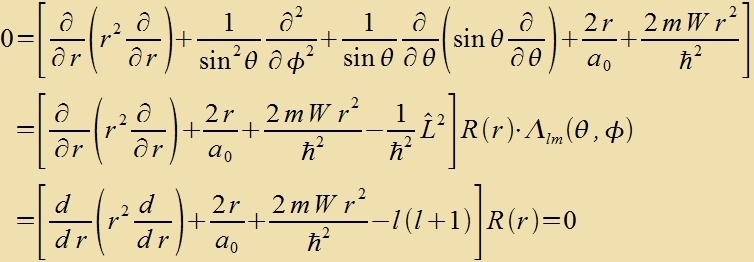
	Vi di Matematik tseigt, zint di Funktsionen (44) di eintsigen stetigen Funktsionen auf einer Kugelfläxxe, di Gleixung (37) erfüllen. Zi zint di Ortsdarctellung (Vellenfunktsion) eines Teilxens mit Bandrehimpulz. Naxdem durx (32/33) unt (44/46) Teile der Gleixung (23) gelözt zint, kann jetst di follctändige Schrödigergleixung für das Elektron imm Vasserctoffatom behandelt verden. Veil di Rexnung nixt relativistic ist, vird angenommen, dass vi imm Bohrcen Atommodel allein durx untercidlixxe Drehimpulze di Energinivos Wn nixt aufgecpalten verden. Deshalb verden di Lözungsanzätse (28) unt (29) viderholt. Auserdem ist es üblix unt tsvekkmäsig, di Potents xl aptsucpalten. 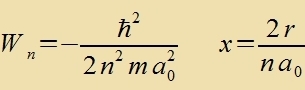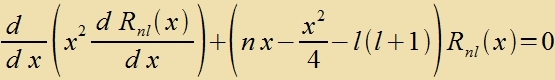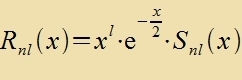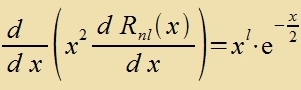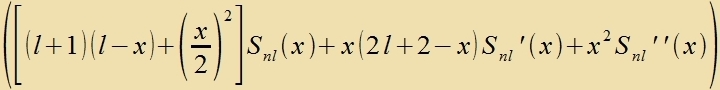ergibt unt mit dem Anzats erhält man tsunäxst Eingezetst inn (46) entcteht di Differentsialgleixung	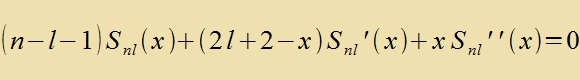(49) (50) (53)
	Für l=0 geht Gl. (53) über inn Gl. (29). Di Lözungen fon (53) zint di tsugeordneten Laguerre-Polünome Snl(x), für di es ebenfalls eine Rodriguez-Formel gibt. 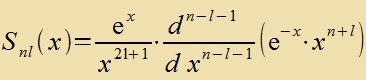alzo 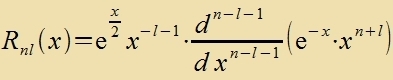Imm Anhang vird als Beicpil getseigt, dass R 7;4 (x) Gleixung (50) erfüllt.	(54)
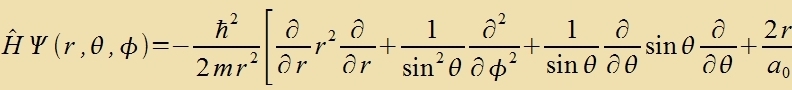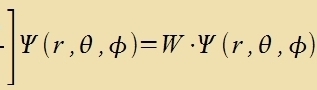
	Ergebnis Di Schrödinger-Gleixung für das Elektron imm Vasserctoffatom hat mit den gantstsaligen Kvantentsalen n, l, m (n≥1, n>l≥0, ∣m∣≤l ) di Lözung	(55) (56)
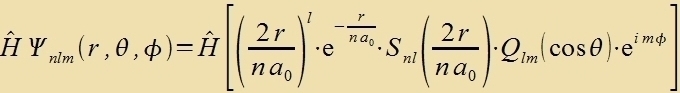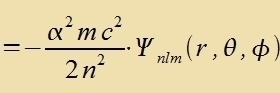
	Dabei ist Snl durx Gleixung (54a) unt Qlm durx di Gleixungen (43) gegeben. Di Konstanten inn dizen Gleixungen zint das redutsirte Planckce Virkungskvantum ħ, di Masse des Elektrons m, der Bohrce Radius a0, di Sommerfeldce Feinctrukturkonstante α unt di Lixtgecvindigkeit c. Eigenfuktsionen tsu Differentsialoperatoren können grundzätslix mit jedem Faktor multiplitsirt verden, one ire Eigencaft als Eigenfunktsion dizes Operators tsu ferliren. Um zi tsu normiren vird ferlangt, dass das Integral über den Definitsionsbereix ∫ψ*∙ψdV gleix 1 zei. Zolxe Normirugen zint imm Anhang angegeben unt in Beicpilen naxgerexnet. 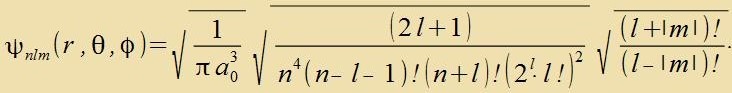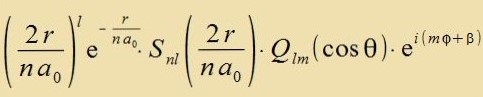Di normirte Vellenfunktsion des Elektrons imm Vasserctoffatom ist demnax Bei der elektromangneticen Velle becreibt di Vellenfunktsion das elektrice oder das mangnetice Feld unt das Kvadrat des Feldes ergibt di Intenzität der Ctralung. Dize Intenzität ist etva beim Lixt di Tsal der Fotonen. Venn di Velle als komplekse Funktsion dargectellt vird, ist di Intenzität das Produkt aus den beiden tsu einander konjugirt kompleksen Funktsionen. Analog datsu ctellt das Produkt ψ*(r)⋅ψ(r) der normirten Vellenfunktsionen di Varceinlixkeit dar, das Elektron am Ort r antsutreffen. Di Normirung bedeutet, das Elektron befindet zix mit Zixxerheit imm Definitsionsbereix der Vellenfunktsion. Eine vixtige Eigencaft der Funktsionen ψ(r) ist ire Zümmetri, insbezondere ir Ferhalten bei einer Cpigelung am Urcprung (Inverzion). Man zagt, eine Funktsion hat gerade Parität, venn ψ(-r)=ψ(r) ist unt ungerade Parität, venn ψ(-r)=-ψ(r) ist. Das Produkt tsveier Funktsionen hat gerade Parität, venn di Paritäten der beiden Faktoren gleix zint, unt ungerade Parität, venn di Paritäten der Faktoren ferciden zint. Veil r inn ψ(r)=ψ(r,θ,φ) immer pozitiv ist unt bei der Inverzion erhalten bleibt, vird di Parität fon ψ(r) allein durx di Kugelfläcxxenfunktsionen Λ l,m(θ,φ) bectimmt. Bei Inverzion geht Λ l,m(θ,φ) über inn Λ l,m(π-θ,φ+π). 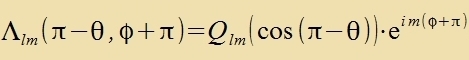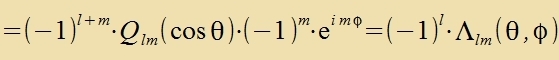ψnlm(-r) hat gerade Parität bei geradem l unt ungerade Parität bei ungeradem l.	(58)
	Ctat der Vellengleixung ψ(x,t), di hir mit Gleixung (1) als Ausgangspunkt der Kvantenmexanik tsugrunde gelegt vurde, kann genau zo gut di konjugirt komplekse Gleixung ψ*(x,t) als Ausgangspunkt gevält verden. Dan ist inn allen Differentsialoperatoren erster Ordnung i durx -i tsu erzetsen, entcprexxend muss di tseitaphengige Schrödingengleixung etvas modifitsirt verden. Dagegen bleibt der Hamilton-Operator ungeändert, veil (-i)²=i²=-1 ist, zodas aux di Eigenverte der Energi der ctatsionären Tsuctände inn dizem unt den folgenden folgenden Kapiteln ungeändert bleiben. Inn der Vellenmexanik des Vasserctoffatoms zint einige Printsipien erkennbar, di inn der gezamten Kvantenmexanik gültig zint. 1. Beopaxtbare füzikalice Grösen - Opzervable - verden durx Operatoren repräzentirt. Inn der Vellenmexanik zint das Differentsialoperatoren. 2. Di möglixxen Verte einer Opzervablen zint Eigenverte des entcprexxenden Operators. 3. Di möglixxen Tsuctände eines Züstems verden durx di Eigenfunktsionen der entcprexxenden Operatoren dargectellt. 4. Eigenfunktsionen eines Operators tsu fercidenen Eigenverten zint tsu einander ortogonal. 5. Di normirten Eigenfunktsionen eines Operators bilden di ortonormale Bazis eines Hilbertraumes. 6. Das Produkt ψ*∙ψ normirter Eigenfunktsionen ist eine Varceinlixkeitsdixte. 7. Di Faze einer Eigenfunktsion kann veder durx den Operator nox durx di Normirung festgelegt verden. Zi vird vixtig bei der Überlagerung fon Tsuctänden. 8. Der Hilbertraum fon Operatoren mit untercidlixxen Hilberträumen ist das direkte Produkt der Hilberträume (Beicpil: Hilbertraum für Rnl unt Λlm). 9. Di Eigenfunktsionen aus untercidlixxen Hilberträumen verden imm gemeinzamen Hilbertraum miteinander multiplitsirt. Historices: Erwin Schrödinger unterzuxte for etva hundert Jaren ausgehend fon de Broglies Vellenforctellung, velxe Funktsionen di Materievelle eines Elektrons imm radialzümmetricen Feld des Atomkerns becreiben. Aus der Matematik var bekannt, dass jede zolxe Funktsion inn eine Ortogonalreihe entvikkelt verden kann, vobei di Laguerre-Polünome unt di Kugelfläxxenfunktsionen di Bazis bilden. Veil dize Bazisfunktsionen zelpst als Eigenfunktsionen fon Differentsialoperatoren tsu Eigenverten gehören, di den Bohrcen Energinivos entcprexxen, entdekkte Schrödinger di Vellenmexanik. Er konnte etvas cpäter tseigen, dass di Vellenmexanik unt Heisenbergs Matritsenmexanik nur tsvei fercidene Darctellungen der gleixen Kvantenmexanik zint.
A