 Füzik |  Home | XXVI. Kvantenfüzik |  | Porträ (bearbeitet) Fundctelle |
 Füzik |  Home | XXVI. Kvantenfüzik |  | Porträ (bearbeitet) Fundctelle |
Nax einer Umfrage unter Füzikern ist der Doppelcpaltferzux mit Elektronen das cönste füzikalice Eksperiment. Bei dizem Ferzux verden eintselne Elektronen mit genau gleixer Gecvindigkeit auf einen Doppelcpalt gecossen unt dahinter detektirt. Nax der angegebenen Antsal fon Elektronen entctehen folgende Bilder.
| Fundctelle | |||||||||||||||||||||||
Nax der zogenannten Kopenhagener Deutung der Kvantenmexanik gibt es für di Orte, an denen di Elektronen auftreffen können, eine bectimmte Varceinlixkeit unt dize Varceinlixkeitsfunktsion hat di Form einer Vellengleixung. Ist di Varceinlixkeitsvelle für beide Cpalte gleix, trifft alzo das Elektron mit gleixer Varceinlixkeit auf einen der beiden Cpalte, dan interferirt di Varceinlixkeitsvelle hinter dem Cpalt inn gleixer Veize vi eine Lixtvelle. Es ist unmöglix, naxträglix festtsuctellen, durx velxen Cpalt das Elektron geflogen ist, unt jeder Ferzux, forher festtsulegen oder tsu messen, durx velxen der beiden Cpalte das Elektron fligt, tserctört di Varceinlixkeitsvelle, zo vi beim Lixt di Ausleuxtung nur eines Cpalts keine Doppelcpalt-Interferents ergibt. Mit den geometricen Daten des Ferzuxs unt der Intenzitätsferteilung am Doppelcpalt (Gl. (4) Kapitel XIII) erhält man eine Vellenlänge für di Elektronen.
|
| |||||||||||||||||||||||
Da es für dize Vellen keinen allgemein ferbindlixxen Ausdrukk gibt, vird hir der Ausdrukk Materievelle veiter benutst. Materievellen zint heute für file Arten fon Korpuskeln unter anderem durx Doppelcpaltferzuxe naxgevizen.
|
| |||||||||||||||||||||||
Ein Korpuskel kann aus einer zolxen Kvantenban herausgeclagen verden oder zi aus anderen Urzaxxen ferlassen. Aber zolange es inn der Kvantenban bleibt, ist der Ort, vo es zix gerade befindet, grundzätslix nixt festctellbar. Inn der klassicen Füzik müsste ein geladenes Korpuskel auf einer Kreizban eine elektromangnetice Velle apctralen. Aux das ist auf einer Kvantenban nixt möglix, da aus dizer Velle di Ortsdaten des Korpuskels festctellbar vären.
| Fundctelle | |||||||||||||||||||||||
Um 1900 entdekkte Rutherford, dass di Ctralung des Uran aus drei fercidenen Arten becteht - der elektric pozitiven α-Ctralung, der negativen β-Ctralung unt der neutralen γ-Ctralung. Er becoss eine dünne Goldfolie mit α-Ctralen unt fand, dass der veitaus gröste Teil der Ctralung ungehindert hindurx flog, ein kleiner Teil aber ser ctark gectreut vurde. Daraus closs er, dass di Masse der Atome imm vezentlixxen inn einem zer kleinen Kern kontsentrirt var. Da bei zeltenen Ereignissen zogar α-Ctralung tsurükprallte, musste der Atomkern pozitiv geladen zein. Di Forctellung lag nahe, dass di negativen Elektronen um dizen pozitiven Atomkern kreizen könnten vi di Planeten um di Zonne. Aber inn der klassicen Elektrodünamik ctralt eine elektrice Ladung auf einer Kreizban vi bei jeder Cvingung ctändig Energi inn Form einer elektromangneticen Velle ap. Dizes Problem lözte Bohr, indem er one Begründung ctabile Kvantenbanen postulirte, auf denen das Elektron keine Velle apctralt. Dize Bohrcen Banen entcprexxen der Gleixung (2). Zetst man inn einer kreizförmigen Kvantenban di Tsentripetalkraft (Kapitel IV, Gl.(18)) gleix der Kraft auf eine negative Elementarladung imm Feld einer pozitiven Kernladung QK (Kapitel XVI, Gl.(11)), zo erhält man 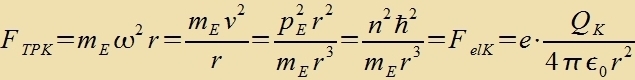 Daraus folgt für den Radius einer Kvantenban des Vasserctoffatoms (QK = e)
|
| |||||||||||||||||||||||
α ist di dimenzionsloze Sommerfeldce Feinctruktur-Konstante, a0 der Bohrce Radius unt n eine gantse Tsal. Es ist α=0,007297≈1/137 unt a0=5,29∙10-11m.
|
| |||||||||||||||||||||||
W=-W1 ist di Energi, di nötig ist, um das Elektron aus dem Vasserctoffatom imm Grundtsuctand tsu lösen, es ist di Ionizatsionsenergi des Vasserctoffs. Energien dizer Grösenordnung verden inn Elektronenvolt angegeben. 1eV ist di Energi, di ein Elektron gevinnt, venn es di Potentsialdifferents 1V durxläuft. 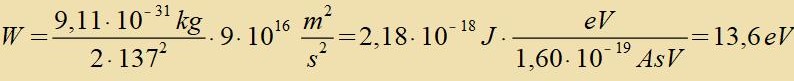
|
| |||||||||||||||||||||||
|
| |||||||||||||||||||||||
Di Ferbesserung des Auflözungsfermögens inn der Cpektroskopi fürte tsur Endekkung fon Feinctrukturen. Cpektrallinien, di forher als eine Linie apgebildet vurden, erceinen nun als eng benaxbarte Linien, Multipletts genannt. Di Erklärung geht dafon aus, dass bei einer Hauptkvantentsal n>1 di Bedingung für eine Kvantenban (Gl. (2)) aux fon kleineren gantsen Tsalen als n erfüllt vird. Ancaulix handelt es zix um Ellipsenbanen (der Kreiz ist hir eine cpetsielle Ellipse), di alle di gleixe grose Halbakse (gleixes n), aber fercidene Drehimpulze bezitsen. Das allein kann allerdings keinen Untercid inn der Energi dizer Ellipsenbanen erklären; denn vi bei den Planeten (Kapitel V) haben alle Ellipsenbanen mit der Hauptkvantentsal n - alzo gleixer groser Halbakse - di gleixe Gezamtenergi.
Di Ausvalregel bedeutet, dass der Drehimpulz des Elektrons bei der Emission eines Fotons um ħ geändert vird. Aus der Konstants des Drehimpulzes folgt dan veiter, dass das Foton den Drehimpulz ħ bezitst unt dass umgekert dizer Drehimpulz des Fotons di Urzaxxe für di Ausvalregel Δl=∓1 ist. Andere Übergänge des Elektrons zint nixt grundzätslix unmöglix (ferboten), zi kommen aber bei der Emission oder Apzorptsion eines Fotons nixt for. |
| |||||||||||||||||||||||
Con einige Jare befor di erste Kvantenhüpotese fon Planck aufgectellt vurde, hat Zeemann di Aufcpaltung der Cpektrallinien inn einem äuseren homogenen Mangnetfeld entdekkt. Dize Aufcpaltung ist immer proportsional tsur Feldctärke B unt beim zogenannten normalen Zeemaneffekt (Beicpil Cd) ist der Proportsionalitätsfaktor immer gleix. Als Erklärung kommt nur di potentsielle Energi eines mangneticen Moments inn dizem Mangnetfeld inn Frage. Ein zolxes mangnetices Moment μ encteht durx den Ctrom, den das Elektron auf einer Kreizban darctellt. Es zei U der Umfang der Ban, A di Fläxxe unt T di Umlaufstseit auf einer Kreizban mit der Hauptkvantentsal n. Es gilt μ=I∙A (Gl. (7) Kapitel XVIII)
|
| |||||||||||||||||||||||
μB∙B lifert den rixtigen Betrag für di Aufcpaltung der Energinivos beim normalen Zeemann-Effekt. Di Hauptkvantentsal n ist aber an dizer Ctelle falc! Di Cpektrallinie für den Übergang fon n=2 nax n=1 cpaltet beim normalen Zeemann-Effekt inn drei Linien auf. Das fürt tsur Anname, dass das Nivo für n=1 einfaxx bleibt unt das Nivo für n=2 inn drei Nivos aufcpaltet. Inn der klassicen Rexnung (Gl. (13) Kapitel XVII) geht es um di Projektsion des mangneticen Momentes auf di Rixtung des Feldes, -cos(φ) läuft fon -1 bis +1 für φ fon 0 bis π. Alle Verte fon -μ∙B bis +μ∙B vären nax klassicer Rexnung möglix, das vären für n=2 alle Verte fon -2μB∙B bis +2μB∙B. Tatzäxxlix kommen aber nur di drei Verte -μB∙B, 0 unt +μB∙B for. Eine dritte Kvantentsal ist nötig. Da das mangnetice Moment fom Drehimpulz bectimmt vird, muss di mangnetice Kvantentsal m auf di Nebenkvantentsal l tsurükgefürt verden. Tsum Drehimpulz (l+1)∙ħ gehört als höxste potentsielle Energi des mangneticen Momentes der Vert l∙μB∙B unt als geringste der Vert -l∙μB∙B, vi das Beicpil für n=2 tseigt. Di mangnetice Kvantentsal m nimt di Verte fon -l bis +l an, das zint 2l+1 gantse Tsalen. Auffällig ist der Tsuzammenhang tsviccen der Nebenkvantentsal l und dem Drehimpulz. Einerzeits zollte der Drehimpulz gleix (l+1)∙ħ zein, andererzeits ist di Projektsion des Drehimpulzes auf di Rixtung des Mangnetfeldes höxstens l∙ħ. Zolxe Ungereimtheiten finden erst inn der Kvantenmexanik eine tsveifelsfreie Lözung. Tatzäxxlix hat das Elektron mit der Nebenkvantentsal l=0 für den Ort des Kerns eine Aufenthaltsvarceinlixkeit gröser als Null, es brauxt den Kern nixt tsu umrunden, zein Drehimpulz ist Null. Aus dizem Grund muss inn Gleixung (9c) di Hauptkvantentsal n durx di Kvantentsal l für den Drehimpulz erzetst verden. Beim zogenannten anomalen Zeeman-Effekt, der tatzäxxlix veit häufiger ist als der normale, verden di Cpektrallinien inn tsvei Linien (Dublett) aufgecpalten. Das ist mit dem Modell der Ellipsenbanen unt der mangneticen Kvantentsal m nixt tsu erklären. Dize Dublettstruktur blib lange Tseit ein Rätsel. Naxdem inn der Xemi di karakterisicen Eigencaften der Elemente tsur Aufctellung des Periodenzüstems gefürt hatten, vurde inn der Füzik di Ordnungstsal Z als Kernladungstsal interpretirt. Damit ist aux di Tsal der Elektronen inn der Hülle des neutralen Atoms gegeben. Aux venn das Bohr-Sommerfeldce Atommodell nixt übertragen verden kann auf Atome mit mer als einem Elektron, kann der Aufbau der Elektronenkonfiguratsion filfaxx aus den Cpektren der Atome mithilfe der Kvantentsalen geklärt verden. Datsu ist allerdings nox eine vezentlixxe Anname nötig: das "Pauli-Ferbot" erlaubt höxstens tsvei Elektronen auf der gleixen Ban. Banen der Elektronenhülle verden tsu Calen tsuzammengefasst unt dize mit der Hauptkvantentsal n nummerirt. Di erste Cale hat nur di Ban 1s (n=1 unt l=0), zi ist mit tsvei Elektronen aufgefüllt. Di tsveite Cale hat eine 2s-Ban (n=2, l=0) unt drei 2p-Banen (n=2,l=1 unt m=-1,0,+1), zi ist mit 4∙2=8 Elektronen aufgefüllt. Helium (Z=2) hat eine aufgefüllte Cale (n=1), Neon (Z=10) hat tsvei aufgefüllte Calen, di erste mit 2 unt di tsveite mit 8 Elektronen. Veil dize Edelgazkonfiguratsionen inn zix bezonders ausgeglixxen unt ctabil zint, ist das jeveils näxste Elektron relativ lokker an das Atom gebunden: di Atome der Alkali-Gruppe (Li, K, Na...) geben zer leixt ir äuserstes Elektron, das Leuxtelektron ap.
Stern unt Gerlach zuxten eine Antvort auf di Frage, op di Rixtungskvantelung - di Kvantentsal m - eine rein teoretice Erklärung der Cpektren imm Mangnetfeld zei oder op zi real räumlixxe Bedeutung hätte. Das Ergebnis ires Ferzuxs gab eine eindeutige Antvort, varf aber neue Fragen auf. Da es imm Stern-Gerlach-Ferzux keine Atome gibt, di nixt apgelenkt verden, zint di Kvantentsalen l unt m des Elektrons, das di Aplenkung ferurzaxxt, gleix Null; denn di Projektsion eines Bandrehimpulzes auf di Rixtung des Mangnetfeldes hätte tsu einer 2l+1-faxxen Aufcpaltung mit gantstsaligem l füren müssen, nixt tsu einer Aufcpaltung inn tsvei Ctralen. Es muss eine neue Kvantentsal eingefürt verden, di, um den Stern-Gerlach-Ferzux tsu erkären, nur tsvei Verte fon gleixem Betrag - einen pozitiven unt einen negativen - annimt. Dize neue Kvantentsal s erklärt dan aux di Dubletts inn den Cpektren unt das Pauli-Ferbot: Elektronen können nixt inn allen Kvantentsalen n, l, m unt s übereinctimmen. Venn imm Bild des Stern-Gerlax-Ferzuxs der untere Ctral z- apgeblokkt vird, können mit dem 'polarizirten' Ctral z+ veitere Ferzuxe durxgefürt verden. Mit SGz+ zei das skitsirte Mangnetfeld betseixnet, mit SGz- ein Stern-Gerlax-Feld, das um 180° um di x-Akse gedreht ist, unt mit SGy+ ein um 90° gedrehtes Feld.
Es dauerte einige Jare, bis tsvei niderländice Ctudenten - Uhlenbeck unt Goudsmit - eine Erklärung fanden, di inn der Kvantenmexanik foll bectätigt vird. Elektronen haben einen Eigendrehimpulz - einen Spin - unt ein datsu gehörendes mangnetices Moment. Di Spinkvantentsal s nimt di Verte +1/2 unt -1/2 an, der Eigendrehimpulz des Elektrons ist s∙ħ unt das mangnetice Moment μ=gs∙s∙μB. Dabei ist gs der zogenannte Landè-Faktor, er ist gleix 2 (genauer gs=2,0023). Das güromangnetice Ferhältnis, das Ferhältnis tsviccen Drehimpulz unt mangneticem Moment, ist für den Spin des Elektrons doppelt zo gros vi für zeinen Bandrehimpulz. Cpäter gelang es Stern mit der gleixen Ferzuxsanordnung, tsu tseigen, dass ein Ctral fon Vasserctoffmolekülen H2 tsvar nixt aufgecpalten, aber dox ferbreitert vird. Da di beiden Elektronen bei dizer kovalenten Bindung eine gemeinzame Ban um di beiden Kerne bezetsen, zint notvendigerveize ire beiden Spins entgegengetst gerixtet unt daher mangnetic unvirkzam. Di Urzaxxe der Ferbreiterung zint di Spins unt mangneticen Momente der beiden Atomkerne des H2, venn deren Spins gleix gerixtet zint (Orto-Vasserctoff). Zo var aux di Eksistents eines Kernspins naxgevizen unt das mangnetice Moment des Vasserctoffkerns venigstens grob apgecätzt. Nax veiteren Ferbesserungen konnte ein Ctral polarizirter H2-Moleküle ausgeblendet verden. Mit einem tsveiten inhomogenen Mangnetfeld, dessen Gradient dem des ersten entgegengezetst gleix ist, ctand eine Messanordnung tsur Ferfügung - Kvelle, Polarizator, Analüzator - di imm Printsip bis heute genutst vird.
Imm Fall der Rezonants gilt auserdem h∙fL=γPℏ∙B=μP∙B, das ist genau di Energi ΔW, di einem Protonenspin den Cprung fom unteren Energinivo auf das obere ermöglixt. Rabi fand di Metode der Kernspinrezonants. Der Polarizator einer Ferzuchsanordnung nach Stern ertseugt einen Ctral polarizirter Moleküle, di imm Analüzator fokussirt unt naxgevizen verden. Tsviccen Polarizator unt Analüzator fligen di polarizirten Moleküle durx ein homogenes Mangnetfeld B unt das Feld BHF(t) einer Cpule. Venn di Frekvents des Vekselctroms durx di Cpule mit der Larmorfrekvents übereinctimmt, verden Moleküle umpolarizirt unt nixt mer imm Analüzator naxgevizen. Aus dizer Rezonantsfrekvents unt dem Vert des Mangnetfeldes B vird das güromangnetice Ferhältnis des Protons bectimmt. Veiterentvikklungen der Metode fon Rabi füren u. a. tsu modernen Atomuren.
| Fundctelle der Kernspinaufname | |||||||||||||||||||||||
| A | ||||||||||||||||||||||||