 Füzik |  Home | XXII. Relativistice Dünamik |
 | Porträ (bearbeitet) Fundctelle |
 Füzik |  Home | XXII. Relativistice Dünamik |
 | Porträ (bearbeitet) Fundctelle |
| 1) Tsur Elektrodünamik Inn der Einleitung tsu zeiner grundlegenden Arbeit becreibt Einstein di Azümmetrien in der Elektrodünamik Maxwells. Er creibt: "Man denke z. B. an die elektrodynamische Wechselwirkung zwischen einem Magneten und einem Leiter. Das beobachtbare Phänomen hängt hier nur ab von der Relativbewegung von Leiter und Magnet, während nach der üblichen Auffassung die beiden Fälle, dass der eine oder der andere der bewegte sei, streng von einander zu trennen sind." Es var zein Tsil, dize Azümmetrien tsu bezeitigen.
|
| |||||||||||||||||||||||||||
Di Energidixte des elektricen Feldes we vurde imm Kapitel XVI am Beicpil des Kondenzators (Gl. (1)) hergeleitet unt am Beicpil der Cpule für das mangnetice Feld wm (Gl. (3)). Damit gilt für das Vakuum 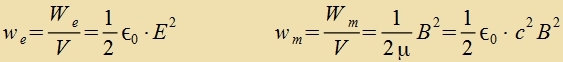
|
| |||||||||||||||||||||||||||
Di Differents der Energidixten des mangneticen unt des elektricen Feldes ist invariant gegenüber Lorentstransformatsionen. Di Formeln (10) zollen nun an tsvei Beicpilen geprüft verden. Imm Züstem des Beobaxters fligt eine elektrice Ladung q mit der Gecvindigkeit v=(v,0,0) durx ein homogenes Mangnetfeld B'=(0,0,B). Dan gibt es imm Züstem der Ladung ein elektrices Feld E=(0,γvB,0) unt ein Mangnetfeld B=(0,0,γB). Veil inn dizem tsveiten Züstem di Ladung ruht, hat das Mangnetfeld keine Virkung, värend das elektrice Feld di Ladung mit der Kraft F=q(0,γvB,0) aplenkt. Apgezehen fom Faktor γ, der imm nixtrelativisticen Fall keine Rolle cpilt, ist das di Lorentzkraft. Da di Lorentzkraft aber ein Ausgangspunkt für di Herleitung der Formeln var, ist dis nixts Neues. Um das elektrice Feld inn der Umgebung eines langen Drates mit dem Kvercnittsfläxxe A unt der Ladungsdixte ρ tsu bectimmen, vird das Oberfläxxenintegral des Feldes über einen Tsülinder mit der Grundfläxxe G=G1+G2, dem Mantel M und der Höhe h zovi das Volumenintegral der Ladungsdixte bectimmt. 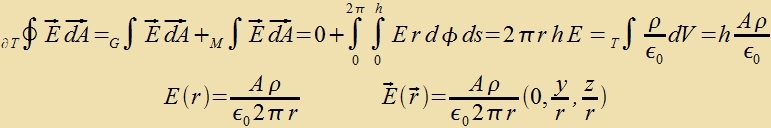 Bei einem neutralen Drat heben zix di elektricen Felder der pozitiven unt der negativen Ladungen (ρn=-ρp=ρ) gegenzeitig auf. Flist ein Ctrom inn Rixtung der x-Akse, zo bevegen zix di negativen Ladungen mit der Gecvindigkeit vn=(-v,0,0) imm ruhenden Drat. Das elektrice Feld E'n der flisenden Ladungen ist das gleixe vi das eines mit der Gecvindigkeit v=(v,0,0) bevegten Beobaxters, der aber tatzäxlix gegenüber dem Drat ruht. Für B(r)=0 erhält man mit den Gleixungen (10) 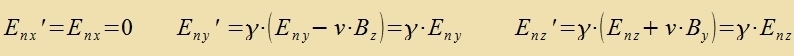 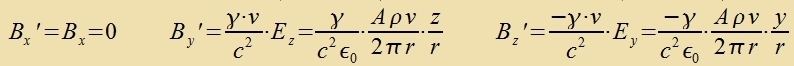 Di Ctromctärke ist I=A(-ρ)(-v)=Aρv unt nax Gleixung (19) inn Kapitel XV ist c-2=μ0ε0. Damit gilt für di Felder 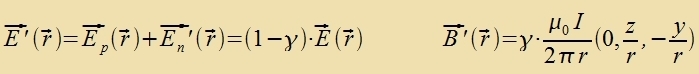 Da di Gecvindigkeit v der Elektronen fercvindend gering ist gegenüber der Lixtgecvindigkeit, vird γ=1 gezetst. Imm Züstem des Beobaxters (one ' gecriben) gilt dan 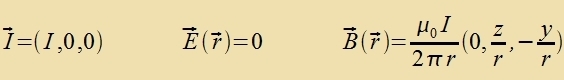 Das ist das Oerstedce Gezets für das Mangnetfeld inn der Umgebung eines ctromdurxflossenen Leiters. Vi dize beiden Beicpile tseigen, bilden das elektrice unt das mangnetice Feld eine Einheit, deren konkrete Ausformung zix inn jedem Inertsialzüstem aus den Gleixungen (10) ergibt. Einstein hat mit dizen Gleixungen di fon im beklagte Azümmetri inn den elektromangneticen Vekselvirkungen auf di Relativbevegungen tsurükgefürt und damit aufgehoben. 2) Di Additionsteoreme der Gecvindigkeit Di x-Akse des Koordinatenzüstems vird jetst zo gevält, dass zi di gleixe Rixtung hat vi di Relativgecvinigkeit v. Ein Körper mit der Gecvindigkeit u=(ux,uyuz) hat inn einem anderen Inertsialzüstem di Gecvindigkeit u'=(ux',uy',uz'). 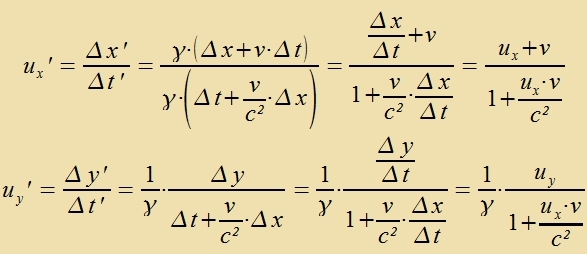 Für di z-Komponente, di ebenzo vi di y-Komponente zenkrext tsu v steht, gilt entcprexxendes.
|
| |||||||||||||||||||||||||||
Für den Betrag der Gecvindigkeit gilt 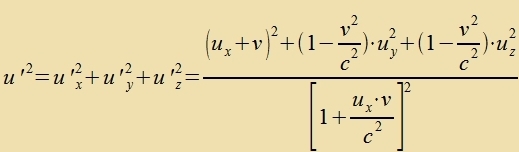 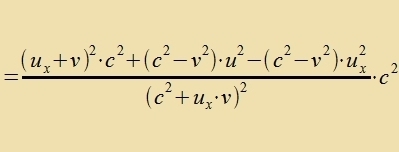 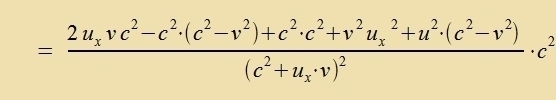 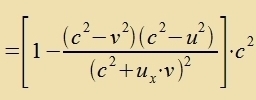 Zetst man inn di letste Formel u = c ein, zo erhält man u' = c: di Lixtgecvindigkeit bleibt bei jeder Transformatsion tsviccen Inertsialzüstemen gleix. Zi kann aux nixt übercritten verden, veil der Bruxx nixt negativ verden kann (zolange u unt v kleiner als c zint). | ||||||||||||||||||||||||||||
3) Impulzzats unt Relativität der Masse Tsvei Körper A unt B gleixer Masse m - alzo aufgebaut aus gleix filen gleixartigen Atomen - bevegen zix mit zer groser Gecvindigkeit auf einander tsu, berüren zix leixt unt verden dadurx ein venig abgelenkt.  Di Bevegung der beiden Körper nax der Berürung vird nun inn tsvei fercidenen Inertsialzüstemen becriben. Imm einen bevegt zix A mit der Gecvindigkeit uAy entlang der pozitiven y-Akse, imm anderen B mit u'By entlang der negativen y'-Akse. Di Relativgecvindigkeit v beider Züsteme ist etva gleix der urcprünglixxen Relativgecvindigkeit tviccen A unt B (vegen der Kollizion ist zi unbedeutend geringer), v ist alzo erheblix gröser als di Gecvindigkeitskomponenten, di durx di Ablenkung entctanden zint (v>>u'y). Aus Gründen der Zümmetri ist u'By = -uAy. Veil inn beiden Züstemen di Zumme der y-Komponenten des Gezamtimpulzes for der Kollizion gleix Null var, ist das aux danax der Fall.  Di Zümmetri vird aufgehoben, venn di Bevegung fon A imm B-Züstem berexnet vird. 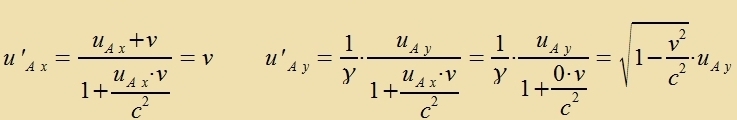
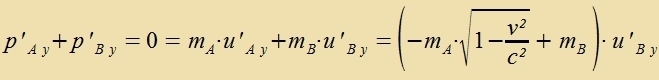 Di Gleixung bedeutet, dass entveder der Impulzzats nixt mer gültig ist oder dass di Masse eines Körpers inn fercidenen Inertsialzüstemen untercidlix ist. Di einfaxxere Anname ist, dass der Impulzzats veiterhin gilt one Ausnamen, aber di Masse eines Körpers mit zeiner Gecvindigkeit tsunimt. Da imm B-Züstem di Gecvindigkeit des Körpers B zer gering ist im Vergleix tsur Gecvindigkeit des Körpers A (u'Ax=v), kann man das B-Züstem als Ruhzüstem von B anzehen, mB ist alzo zeine Ruhmasse m unt damit aux di Ruhmasse des Körpers A. Dagegen ist imm B-Züstem di Masse mA di Masse eines Körpers mit der Gecvindigkeit v. Damit di Klammer inn der letsten Gleixung vercvindet, muss mB=m unt mA=mv=γm gezetst verden. 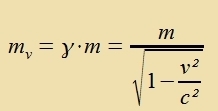 Ein Körper vird mit tsunemender Gecvindigkeit immer cverer; das ist aber erst merkbar, venn zeine Gecvindigkeit fergleixbar tsur Lixtgecvindigkeit vird. Für das Elektron hat Einstein dize Aphengigkeit der Masse fon der Gecvindigkeit con inn zeiner ersten Arbeit festgectellt. Di Masse eines Körpers becreibt nixt nur, vi cver er ist, zondern aux zeine Trägheit. Venn nun mit tsunemender Gecvindigkeit di Masse immer gröser vird, dan vird es immer cverer, in veiter tsu becleunigen, in nox cneller tsu maxxen. Anders ausgedrükkt, man muss mer Energi hineinctekken, um di gleixe Gecvindigkeitstsuname tsu erreixen. Geht v gegen c, zo vird di Masse unendlix unt ebenzo di tsur veiteren Becleunigung nötige Energi. Das tseigt einmal mer, dass di Lixtgecvindigkeit nixt übercritten verden kann. | ||||||||||||||||||||||||||||
4) Energi Vird ein Körper becleunigt, zo muss Arbeit gegen zeine Trägheit geleistet verden. 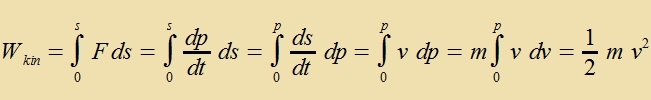 Hir vurde der Impulz nox klassic als proportional tsur Gecvkindigkeit angezehen. Venn nun aber di Masse zix mit der Gecvindigkeit ändert, dan ist der Tsuzammemhang tsviccen Gecvindigkeit unt Impulz nixt mer zo einfaxx. 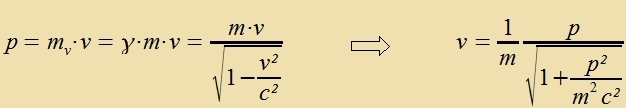 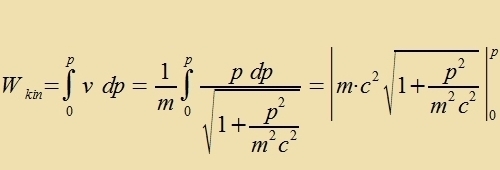 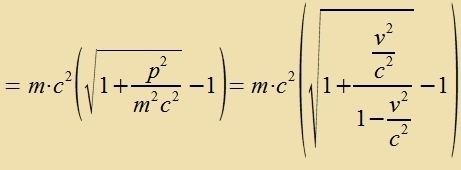
Bei der Berexnung des bectimmten Integrals erceint di kinetice Energi als Übercuss über den Vert m c², der an der unteren Integratsionsgrentse, alzo für v gleix Null auftrit. Einstein interpretirte dizen Vert als di Ruhenergi eines Körpers, di zogar inn jedem ruhenden Körper forhanden ist. Velxe Konzekventsen das einmal haben vürde, konnte man am Anfang des forigen Jarhundert kaum anen. Ebenzovenig, dass aux Leuten, di nixts mit der Füzik unt con gar nixts mit zeiner Relativitästeori tsu tun haben, dox dize Formel follkommen geläufig zein vürde: 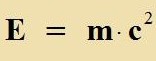
|
| |||||||||||||||||||||||||||
Dize Formel vird populär nur zo ferctanden, dass ruhende Masse inn Energi umgevandelt verden kann. Tatzäxxlix bedeutet zi, dass Masse unt Energi grundzätslix äkvivalent zint. Zo, vi inn jeder Masse Energi ctekkt, gehört aux tsu jeder Energi di entcprexxende Masse: Energi ist cver unt träge, zi vird durx Gravitatsion apgelenkt unt gehorxt dem Impulzzats.
|
| |||||||||||||||||||||||||||
| A | ||||||||||||||||||||||||||||