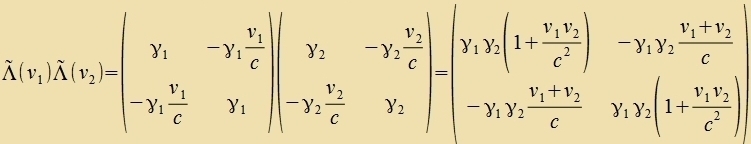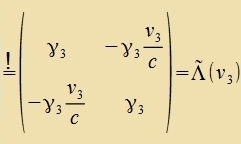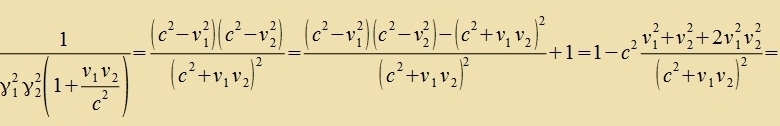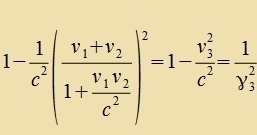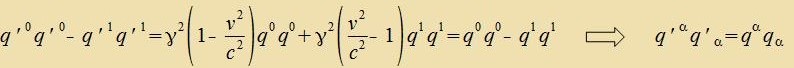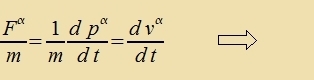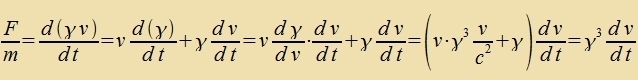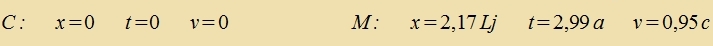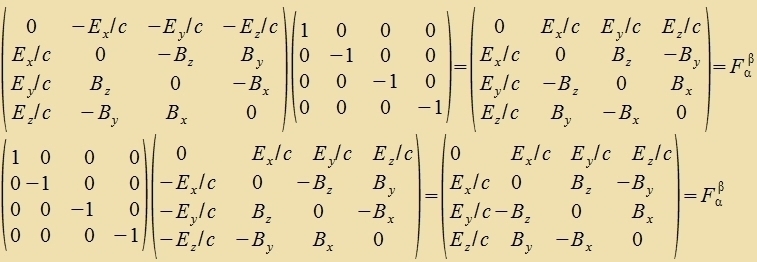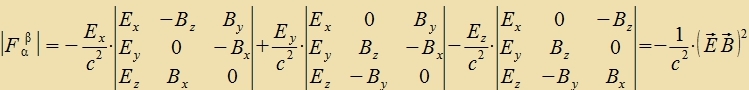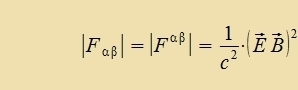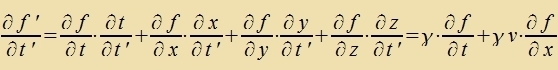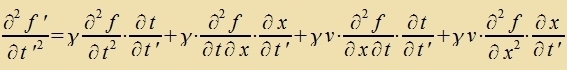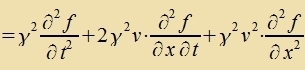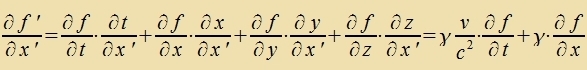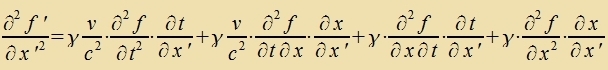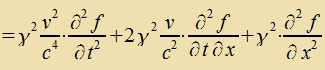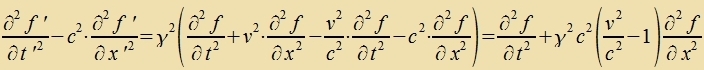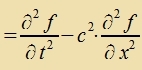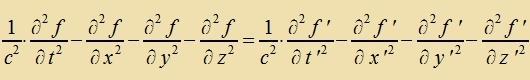|
Durx di Lorentz-Transformatsionen vird der dreidimenzionale Raum tsu einem firdimenzionalen Raum-Tseit-Kontinuum erveitert. Di Punkte
inn dizem linearen Raum, der nax zeinem Entdekker Minkowski-Raum heist, ctellen Ereignisse dar, di an bectimmten Orten unt tsu bectimmten Tseiten (nixt
notvendigerveize) ctatfinden. Minkowski-Diagramme zint Darctellungen inn einem tsveidimenzionalen Unterraum des Minkowski-Raumes, der durx di Relativgecvindigkeit
v tsveier Inertsialzüsteme unt di Tseit t bectimmt ist. Ereignisse unterhalb der x-Akse gehören tsur Fergangenheit, darüber tsur Tsukunft. Ein Ereignis, das fom
Urcprung her nur mit Lixtgecvindigkeit erreixt verden kann, heist lixtartig unt ein Ereignis, das mit einem Körper mit nixt fercvindender Ruhmasse erreixt verden
kann, heist tseitartig.
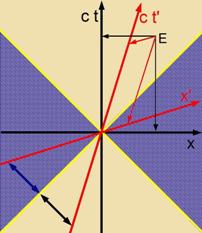 | Inn dizen Minkowski-Diagrammen ist c∙t als Ordinate aufgetragen ctat t, zodas der Masctab beider Aksen
gleix gevält verden kann. Dan ligt der Veg (gelb) des Lixtes, das durx den gemeinzamen Urcprung der Inertsialzüsteme geht, bei jedem Züstem auf der Vinkelhalbirenden
der Koordinatenaksen.
Das unzümmetrice Diagramm links tseigt ein Ruhzüstem (cvarts) mit rextvinkligen Aksen. Das rexte Diagramm ist zümmetric inn beiden
Inertsialzüstemen. Es tseigt di paradokse Zümmetri fon Tseitdilatatsion unt Längenkontraktsion.
Es gibt keinen möglixxen Veg fom Urcprung inn
di blau craffirten Bereixe oder umgekert.
Eingetseixnet ist ein Ereignis E inn tsvei Inertsialzüstemen.
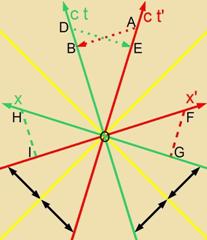
| | OA > OB unt OD > OE tseigen di
Zümmetri der Tseitdilatatsion.
OG < OF unt OI < OH tseigen di
Zümmetri der Längenkontraktsion.
|
| 
|
Inn den Kapiteln XXI unt XXII vurde getseigt, dass alle gegenüber einer Masse, einem Masctab unt einer Ur bevegten Beobaxter di Masse als gröser, den Masctab als geringer
(Längenkontraktsion) unt den Gang der Ur als langzamer (Tseitdilatatsion) beobaxten. Imm Ruhzüstem ist also di Masse am geringsten (Ruhmasse), der Masctab am längsten unt der Gang
der Ur am cnellsten (Eigentseit). Imm linken Minkowski-Diagramm zint beide tsum Ereignis E gehörigen Aksenapcnitte imm Ruhzüstem (cvarts) gröser als imm bevegten Züstem (rot).
Zovol das Tseitintervall tsviccen dem Ereignis imm Urcprung unt dem Ereignis E als aux di Ctrekke datsciccen zint imm Ruhzüstem gröser als imm bevegten Züstem. Der Faktor der
Fergröserung ist immer γ unt der Faktor der Ferringerung 1/γ.
Imm Minkowski-Raum ℝ3+1 ist es imm Gegenzats tsum dreidimenzionalen euklidicen Raum ℝ3 nötig tsu unterceiden, op di Komponenten einer Gröse
bei einer Koordinatentransformatsion zo vi di Koordinatenbazis (kovariant) ferändert vird oder entgegengezetst (kontravariant). Genaueres tsur Kovariants unt Kontravariants
vird becriben im Anhang T: Tenzoren der Raumtseit.
Für di fir Komponenten eines Vektors imm ℝ3+1 zint unter anderem hoxgectellte Inditses üblix, zodas das Produkt Komponente mal Bazisvektor di Form
x1e1 hat. Da hir Potentsen der fir Komponenten immer als Produkt, alzo nixt mit Eksponenten gecriben verden, vird es nixt tsu Fervekslungen
kommen.
Di kontravariante Form ist
Di kovariante Form ist | 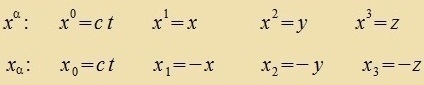 | oder | 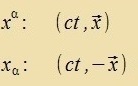
|
|
|
|
| Es gilt di Einsteince Zummenkonventsion: venn inn einem Produkt ein oberer Indeks mit einem unteren Indeks übereinctimmt, vird über alle Verte des Indeks
di Zumme dizer Produkte gebildet. | 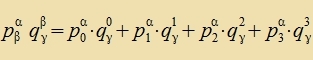
|
Di Lorentz-Transformatsionenen (Kap. XXI Gl. (12)) zint lineare Apbildungen des ℝ3+1 auf den ℝ3+1;
es zint firdimenzionale Koordinatentransformatsionen, di durx 4X4-Matritsen Λ=Λ(v) dargectellt verden. Vird di x-Akse zo gevält, dass
v=(v,0,0) ist, dan gilt
|
|
|
Rexnungen tsu Lorentztransformatsionen mit v=(v,0,0) können auf 2X2-Matritsen becränkt verden. Dis zoll eine Tilde antseigen.
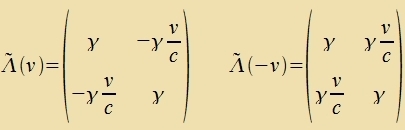 | 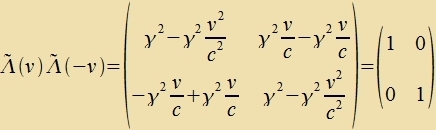 | Vi ervartet ist
Λ(-v) inverz tsu Λ(v).
|
|
|
|
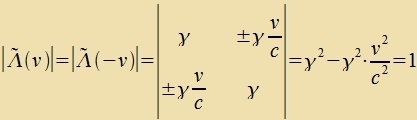 | | Die Determinanten der Lorentztransformatsionen haben den Vert +1.
Vegen cosh2 x - sinh2 x = 1,
kann γ=cosh ζ gezetst verden. | | 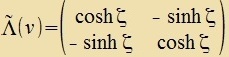
Dis vird for allem inn den Anhängen gebrauxt.
|
Bei drei Inertsialzüstemen Σa, Σb unt Σc, deren Relativgecvindigkeiten parallel zint,
zollen di Inditses 1, 2 unt 3 di Relativgecvindigkeit tsviccen Σa unt Σb, Σb
unt Σc zovi tsviccen Σa unt Σc betseixnen. Venn di Transformatsionen nax einander
ausgefürt verden, verden di Matritsen multiplitsirt.
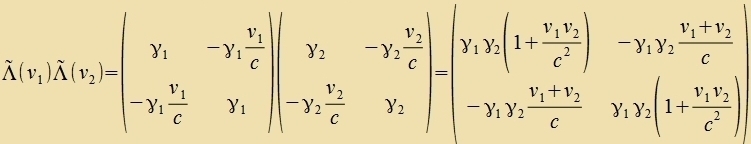 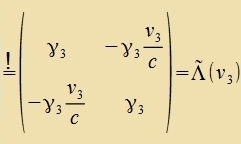
| Durx Fergleix erhält man | 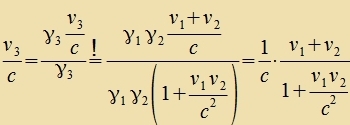 | Dis Ergebnis entcprixxt dem ersten Additsionsteorem der Gecvindigkeiten
(Kapitel XXII, Gl. (19)). Veiter gilt
|
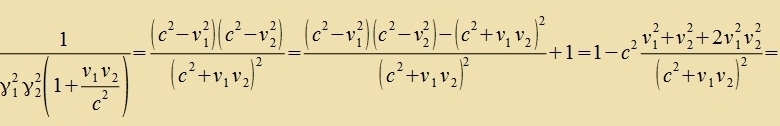 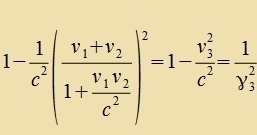
Di Multiplikatsion der Matritsen Λ(v1) unt Λ(v2) fürt tsur
Matriks der ferketteten Lorentz-Transformatsion Λ(v3).
Imm ℝ3 vird der Apctand eines Punktes x fom Urcprung durch di kvadratice Form x2 bectimmt, di unferändert bleibt
bei Drehungen des Koordinatenzüstems. Nun ist für den ℝ3+1 ein firdimenzionaler Apctand gezuxt, der entcprexxend bei Lorentztransformatsionen
unferändert bleibt, 'lorentz-invariant' ist. Dass di einfaxxste Erveiterung c2t2+x2 der kvadraticen Form nixt lorentz-invariant ist, geht nebenbei aux
aus der folgenden Rexnung herfor.
| Es zei Λ(v) qα=q'α. Dan gilt | 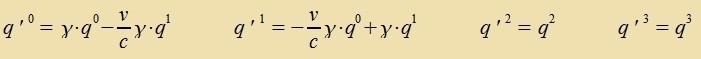
|

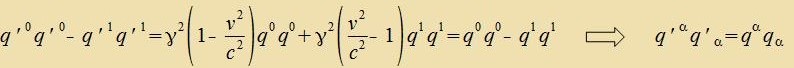
Lorentztransformatsionen lassen di kvaderatice Form qαqα unferändert.
Es gibt einige untercidlixxe Schreibveizen für dize kvaderatice Form.
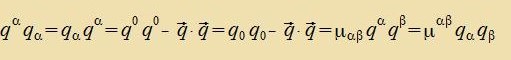 | | 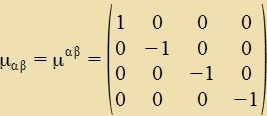 | heist metricen Tenzor.
|
|
|
|
Lässt umgekert eine 4X4-Matriks T mit |T|=1 di kvadratice Form (13) ungeändert, dan folgt
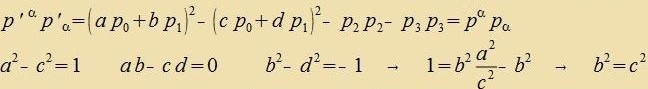
| | 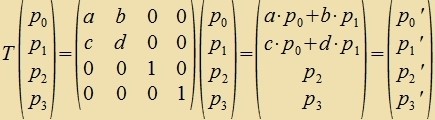
|
a<0 bedeutet eine Umker der Tseit unt d<0 eine Raumcpigelung. Clist man beides aus, dan folgt aus ad=bc, dass b unt c das gleixe Fortseixen haben; aus
b2=c2 folgt dan b=c unt daraus a=d. Auserdem soll gelten |T|=1=ad-bc=a2-b2. Damit cteht di Form fest, di eine 4X4-Matriks
hat, wenn zi di kvadratice Form (13) unferändert lässt (unt veder Tseit nox Raum cpigelt). Es ist eine Lorentztransfomatsion mit v=c∙√(1-a-2)
Bei den Matritsen der räumlixxen Drehungen bleibt di Tseit
unferändert unt damit aux di kvadratice Form. | 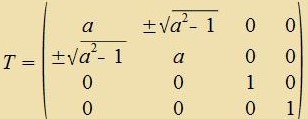
|
Jede (reellvertige) Koordinatentransformatsion imm Minkowski-Raum, di di kvadratice Form (13) invariant lässt, ist eine
Lorentz-Transformatsion
unt jede Lorentz-Transformatsion lässt di kvadratice Form eines Firervektors imm Minkowski-Raum unferändert.
Venn di Koordinaten eines Ereignisses, di inn einem belibigen Koordinatenzüstem des Inertsialzüstems A forligen, inn das Inertsialzüstem B umgerexnet verden zollen,
kann das inn drei Critten gecehen. Tsuerst verden mit Drehmatritsen aus SO(3) di Ortskoordinaten umgerexnet inn ein Koordinatenzüstem fon A, inn dem di
Relativgecvindigkeit tsviccen A unt B parallel tsur x-Akse ligt. Dan verden di Lorentztransformatsionen ("Loretz-boost") angevendet, zodas alle Koordinaten des
Ereignisses inn einem cpetsiellen Koordinatenzüstem des Inertsialzüstems B forligen. Clislix verden di Ortskoordinaten inn ein belibiges Koordinatnzüstem fon B
umgerexnet.
Di kvadratice Form (13) hat di Zignatur (1,3). In der Betseixnung für eine Gruppe fon Transformatsionen, di eine kvadratice Form bectimmter Zignatur unferändert
lassen, vird dize Zignatur übernommen. O(1,3) heist Lorentzgruppe, di Determinanten irer Transformatsionsmatritsen haben den Betrag 1. O(1,3) becteht aus fir
Komponenten, di topologisch nixt tsuzammenhängen, zondern nur durx Cpigelungen verbunden zint. Das neutrale Element der Gruppe kann nur inn einer der fir
Komponenten ligen, nur dize Komponente kann eine Gruppe zein. Eine Untergruppe fon O(1,3) ist di eigentlixe Lorentzgruppe SO(1,3), deren Transformatsionsmatritsen
di Determinante +1 haben. Inn SO(1,3) gibt es Elemente, di di Tseit umkeren. Keine Tseitumker gibt es in der Gruppe SO+(1,3)⊂SO(1,3), der eigenlich
ortoxronen Lorentzgruppe, inn der a=Λ00>0 gilt (fergleixe oben!). Ortoxron bedeutet tseitrixtig, eine tsveite Betseixnung dizer Gruppe ist
L†+. Di eigentlix ortoxrone Lorentzgruppe vird imm Anhang L (Lie-Gruppen)
becriben.
Da di fir Grösen - Tseit unt drei Raumkoordinaten -, di imm Minkowskiraum ℝ3+1 tsu einem Ereignis gehören, imm Gegenzats tsu den Koordinaten imm
ℝ3 untercidlix behandelt verden müssen, können Begriffe nixt one weiteres übertragen verden. Deshalb verden hir di Begriffe Firervektor, Firerort (eines Ereignisses),
Firergröse (Firerimpulz, Firerkraft, ...) unt Firernorm benutst. Der Firerort ist inn (1) unt (2) definirt unt di kvadratice Form (13) zoll di Firernorm einer
Firergröse zein.
Di Firernorm fon xα ist
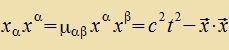
|
| Der raumtseitlixxe Apctand s eines Ereignisses mit dem Firervektor xα fom Urcprung bectimmt zix aus der Firernorm fon
xα. Es zint drei Fälle tsu unterceiden.
|
| 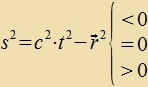
| s imaginär
r = c∙t
r < ct
| keine kauzale Ferbindung
lixtartige Ferbindung
tseitartige Ferbindung
|
Inn Minkowski-Diagrammen begrentst di (gelbe) Lixtlinie das Gebit der Ereignisse, di mit dem Ereignis E0 imm Urcprung inn Vekselvirkung
treten können. Dize Lixtlinie ist der Cnitt des räumlixxen doppelten Lixtkegels mit der x-t-Ebene. Der Urcprung trennt di Ereignisse des Lixtkegels der
Fergangenheit, di als Urzaxxe für das Ereignis E0 inn Frage kommen, fon den Ereignissen des Lixtkegels der Tsukunft, di fom Ereignis
E0 ferurzaxxt verden können.
| Nax Gleixung (17) imm Kapitel XXI ist der Tsuzammenhang tsviccen der Eigentseit τ, di eine Ur an einem festen Plats
inn einem Ruhzüstem antseigt, unt der Tseit t, di eine Ur inn einem anderen Inertialzüstem antseigt, das zix mit der Relativgecvindigkeit v gegenüber dem Ruhzüstem bevegt,
| 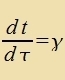 | oder | 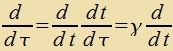
|
Tsur Darctellung der Mexanik imm Minkowskiraum verden di Firervektoren einiger füzikalicer Grösen gezuxt. Um den Firerimpulz pα
tsu bilden, muss di tseitartige Komponente p0 gefunden verden, mit der di Firernorm lorentz-invariant vird. Das gilt nax Gleixung (32)
imm Kapitel XXII für
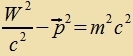 | Daher zint der Firerimpulz unt zeine Firernorm | 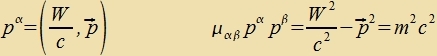
|
| Divizion durx m ergibt di Firergecvindigkeit unt ire Firernorm | 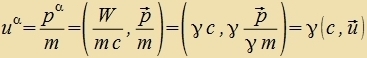 | 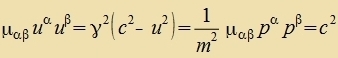
|
|
|
|
Imm Ruhezüstem eines Körpers ist di Firergecvindigkeit (c,0), di Veltlinie ist eine Parallele tsur ct-Akse und es gilt ds=(c,0)dt=(c,0)dτ. Di Betsihung ds=cdτ
ist allgemein, zi hengt nixt fon einem Inertsialzüstem ap, fon dem aus di Veltlinie betraxtet vird.
| Aux imm Minkowski-Raum zoll Newtons Definitsion der Kraft als tseitlixxe Apleitung des Impulzes gültig bleiben. | 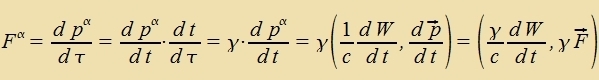
|
| Es gilt | 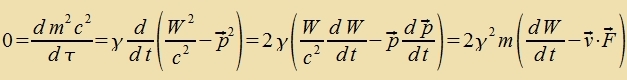 | 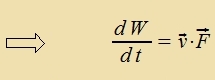
|
| Di Firerkraft unt ire Firernorm zint | 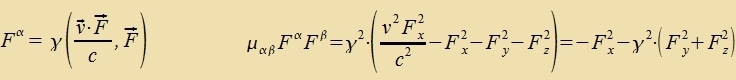
|
|
|
|
Ist di Kraft inn einem Ruhzüstem parallel tsur Relativgecvindigkeit, alzo F=(F,0,0), dan ist di loretz-invariante Firernorm gleix -F2. Der Betrag der Kraft bleibt daher unferändert unt aus
Zümmetrigründen kann keine Kraftkomponente entctehen, di nixt parallel tsur Reltivgecvindigkeit ist. Folglix ergibt di Messung einer Kraft F inn allen Inertsialzüstemen, deren Relativgecvindigkeit
parallel tsu F ist, das gleixe Ergebnis.
Di Gleixung für di Bevegung einer becleunigten Masse fürt an di Grentsen der cpetsiellen Relativitätsteori. Als Beicpil zei eine Masse m momentan inn einem Inertsialzüstem inn Ruhe, das zix mit der
Gecvindigkeit v=(v,0,0) gegenüber dem Ruhzüstem bevegt. Auf den Körper zoll eine Kraft F virken, di parallel tsur Relativgecvindigkeit v ist, zodas F inn dizen
Inertsialzüstemen gleix ist. Jetst zint v unt γ nixt mer konstant, zondern Funktsionen der Tseit.
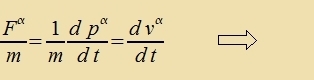 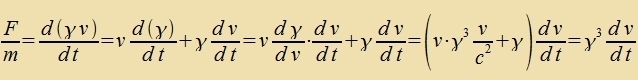
| Veil F parallel tsur Relativgecvindigkeit ist unt deshalb inn allen Inertsialzüstemen unferändert bleibt, ist a=F/m konstant. | 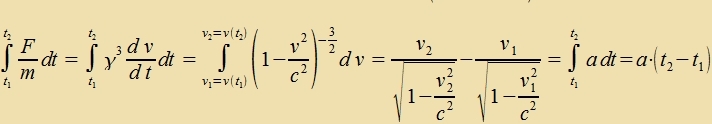
| | Mit t1=0 unt v1=v( t1)=0 erhält man für di Gecvindigkeit einer Masse m bei konstanter Kraft | 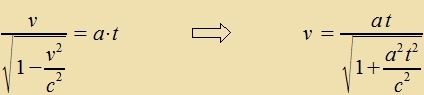
|
Zolange a∙t klein bleibt gegen c, ist vi inn der klassicen Füzik v=a∙t. Vird der Vert fon a∙t fergleixbar tsu c, dan nähert zix v(t) vi ervartet azümptotic der Lixtgecvindigkeit, one zi übertreffen tsu können. Di veiteren Gleixungen für di relativistice Bevegung bei konstanter Kraft zint
Inn erster Ordnung (nax einer Reihenentvikklung für di Vurtseln) ctimmen dize Gleixungen alle mit den Gleixungen der klassicen Füzik überein.
Als Beicpil zoll eine Ekspeditsion tsum Ctern α Centauri durxgerexnet verden. Erde unt Ctern gelten als ruhend, ire Entfernung beträgt d=4,34 Lixtjare. Damit di Astronauten möglixst ctändig ir Erdgevixt
cpüren, zorgt der Motor des Raumciffs für eine Becleunigung a=g. Auf halber Entfernung vird di Rixtung der Becleunigung umgekert, um das Raumciff aptsubremzen. Imm Züstem der Erde gilt für di
Ereignisse C (Ctart) unt M (Mitte der Ctrekke erreixt):
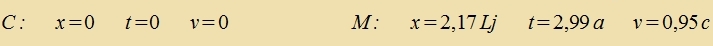
Anders ferlaufen alle Forgänge aus der Zixt der Astronauten, dessen Ur di Tseit T antseigt. Das Raumciff ist
tsvar kein Inertsialzüstem; trotsdem darf für di momentane (infinitezimale) Umrexnung tsviccen den Tseiten Gleixung (17) imm Kapitel XXI entcprexxend angevendet verden.
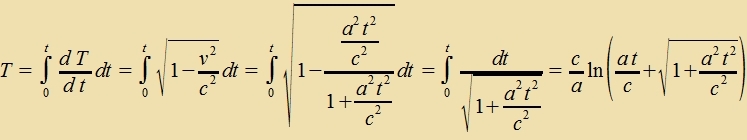 | T(2,99a)=1,79a
|
Di gezamte Reize zetst zix tsuzammen aus fir gleix langen Etappen, venn eine möglixxe Aufenthaltsdauer unberükzixtigt bleibt. Bei irer Rükker zint dan di Astronauten um 7,15 Jare älter
gevorden, värend auf der Erde 12 Jare fergangen zint. Venn das Tsil veiter entfernt ist, väkst diezer Untercid erheblix, veil dan ein gröserer Teil der Reize fast mit Lixtgecvindigkeit geflogen vird unt di
Astronauten auf dizem gröseren Teil der Ctrekke zer langzam leben. Zo vürde eine Reize tsur Beteigeuze fon der Erde aus gezehen rund tauzend Jare, imm Raumciff dagegen 'nur' rund hundert Jare dauern.
Di Kontinuitätsgleixung (Kap. XIII, Gl. (1)) ferbindet di Ctromdixte j mit der Ladungsdixte ρ. Deshalb ligt es nahe, di
Ladungsdixte ρ inn einem Firerctrom jα als tseitlixxe Komponente eintsuzetsen. Venn di Ladung Q eines Volumen A⋅l inn
der Tseit t durx di Fläxxe A flist, dan ist der Ctrom I=Q/t=ρ⋅Al/t unt di Ctromdixte inn der Fläxxe A j=ρ⋅l/t. Dabei ist l/t di Gecvindigkeit,
mit der di Ladung flist, zodas für di Ctromdixte gilt j=ρ⋅v.
| Tsur Ctromdixte j gehört der Firervektor | 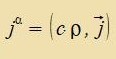 | mit der Firernorm | 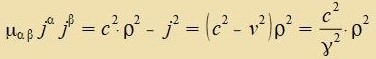
|
Aus dem Firerctrom erhält man di Kontinuitätsgleixung, venn nax dem Firerort differentsirt unt das Ergebnis gleix Null gezetst vird.
| Mit der Creibveize | 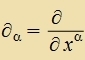 | erhält man | 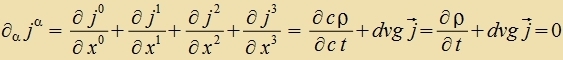 |
|
|
|
|
Dize Creibveize kann als firdimenzionale Divergents angezehen verden. Der Firerctrom beinhaltet di Kontinuitätsgleixung unaphengig fom Inertsialzüstem.
Gleixung (33) kann aber nur für ein apgeclossenes Gebit der Raumtseit gelten, durx dessen Grentsen keine Ladungen ein- oder austreten. Andererzeits brauxen
Parbildung unt Tserstralung nixt tsuzätslix berükzixtigt werden, da zix dadurx di Gezamtladung nixt ändert.
Värend inn der klassicen Füzik di Erhaltung der Masse unt damit eine entcprexxende Kontinuitätsgleixung für Massendixte unt Dixtectrom postulirt verden konnte, ist
nax der Relativitätsteori ein zolxes Postulat erledigt. Masse kann ctatdessen als Erceinungsform der Energi angezehen verden. Aus der Energidixte w unt irer
Ctrömung s vird ein Firervektor gebildet.
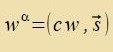 | Inn einem apgeclossenen Züstem vi etva imm Univerzum gilt der Energizats | 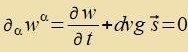
|
|
|
|
Da tsur Energi Masse gehört, ist mit der Energidixtectrömung sx eine Impulzdixte Gxx ferbuden. Der erste
Indeks cteht für di Rixtung der Urzaxxe sx, der tsveite für di Rixtung des Impulzes. Nun ist inn der Energidixte unt damit inn der
Ctrömung sx di elektromangnetice Feldenergi enthalten. Venn dize zix mit sx ändert, gibt es Impulze zenkrext tsur x-Rixtung (Lorentz-Kraft).
Es entctehen drei Firervektoren, aus denen tsuzammen mit wα eine 4X4-Matriks gebildet vird.
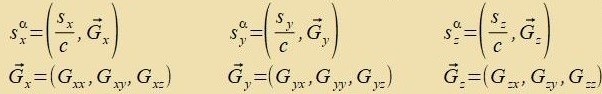 | | 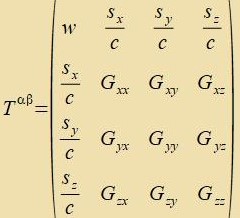 | Tαβ ist der
Energi-Impulz-Tenzor.
|
|
|
|
| siα mit i=x,y,z ist der Firervektor der Impulzkomponente pi. Venn der Zats fon der Impulzerhaltung gilt, ist
| 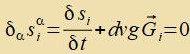
|
| Venn di Divergents des Energi-Impulz-Tenzors fercvindet, | 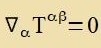 | bleiben Energi unt Impulz inn der Raumtseit erhalten.
|
|
|
|
Es ist unmöglix, das elektrice Feld E oder das Mangnetfeld B als Firervektoren dartsuctellen, veil di zeks Komponenten bei Lorentz-Transformatsionen inn einander
übergehen. Ctatdessen verden für den ctatsionären Fall di drei räumlixxen Komponenten des Vektorpotentsials A mit dem elektricen Potentsial φ als tseitartige Komponente
tsuzammengectellt. Damit di Dimenzionen gleix zint, vird φ durx c dividirt (Tm = N/A = J/As ∙ s/m).
| Mit dem Firer-Potentsial | 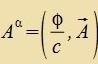 | erhält man | 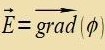 | unt | 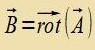
| Die Potentsiale φ unt A zint eichfrei.
|
|
|
|
Eichfreiheit der Potentsiale bedeutet, dass tsu φ(r,t) jedes ψ(r,t) mit grad ψ(r,t)=0 addirt verden kann, onedas E(r,t) zix ändert, unt dass tsu A(r,t)
jedes C(r,t) mit rot C(r,t) addirt verden kann, onedas B(r,t) zix ändert.
| Der Operator | 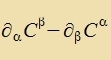 | kann als Erveiterung der Rotatsion gelten. Er ertseugt eine 4X4Matriks | 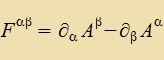 |
|
Es ist Fαα=0 unt Fαβ=-Fβα, es gibt alzo nur zeks unaphengige Komponenten.
Auserdem fercvinden bei einem ctatsionären Feld alle Apleitungen nax x0=c∙t.
| Beicpile für di Berexnung der Matrikselemente: | 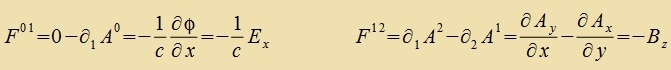
|
| Di Matriks des Feldctärketenzors inn kontravarianter Form ist | 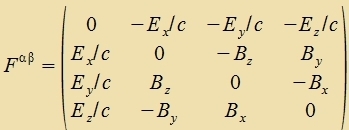 |
|
|
|
|
Der metrice Tenzor μ virkt imm Minkowskiraum vi eine Koordinatentransformatsion für den Übergang fon einer kontravarianten Form inn eine kovariante Form unt
umgekert. Alles, vas zix - eventuell aux nur formal - als Firervektor creiben lässt, vird durx di Matriksmultiplikatsion mit dem metricen Tenzor fon der einen inn
di andere Form überführt. Veil der metrice Tenzor tsu zix zelpst invers ist, ist
μαβ=μαβ

| Für di kovarianten Formen der Potentsiale unt Feldctärken erhält man | 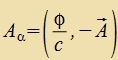 | unt | 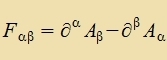 |
|
| unt di Matriks des Feldctärketenzors inn kovarianter Form ist | 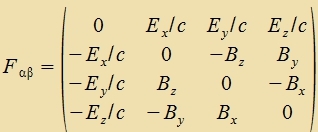 |
|
Venn ctat der Einsteincen Zummenkonventsion di Multiplikatsion fon Matritsen genutst vird, muss auf di Reihenfolge der Matritsen geaxtet verden.
 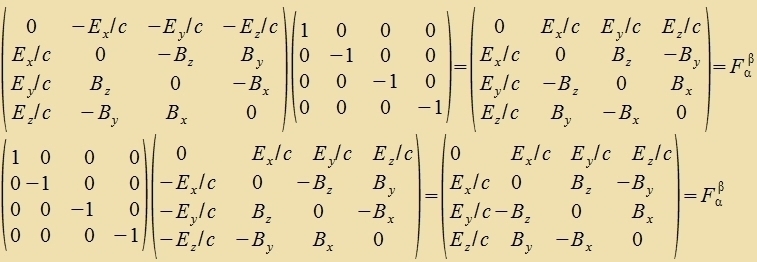
Veil di Determinante des metricen Tenzors gleix -1 ist, gilt für di Determinanten der Feldctärketenzoren
|Fαβ|=-|Fαβ|=|Fαβ|. Es ist
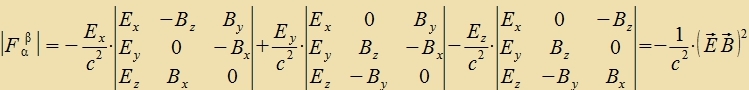 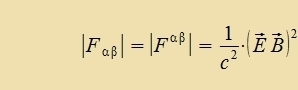
|
|
|
Dize Determinanten zint lorentz-invariant, da di Determinanten der Lorentztransformatsionen gleix eins zint. Auserdem gilt
| 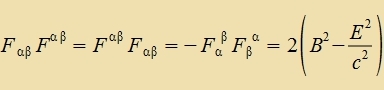 | Nax Gleixung (13) imm Kapitel XXII ist dizer Ausdrukk lorentz-invariant. |
|
|
|
|
Venn imm dreidimenzionalen Raum eine Koordinatentransformatsion T durxgefürt vird, vird eine Matriks A nax der Regel
A' = T A T-1 transformirt. Überträgt man das auf den Minkowski-Raum, zo erhält man für di Koordinatentransformatsion
des Feldctärketenmzors
Dize Transformatsion des Feldctärketenzors Fαβ entcprixxt foll den Gleixungen (10) imm Kapitel
XXII. Der Tsuzammenhang tsviccen dem elektromangneticen Feld unt den Dixten fon Ladung unt Ctrom kann jetst inn einer kompakten Form gecriben
verden.
| Mit | 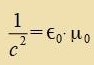 | unt | 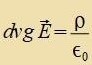 | unt | 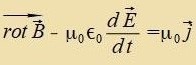
| (nax Gleixung (12) imm Kapitel XVIII) erhält man | 
|
| Imm Vakuum mit ρ=0 unt j=0 folgt | 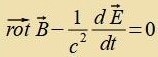 | unt vi Gleixung (13) inn Kapitel XVIII gilt
| 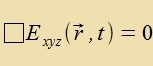
|
|
|
|
Vi imm Kapitel XVIII Elektromangnetice Vekselvirkungen folgen daraus di Vellengleixungen für di Komponenten des elektricen
und des mangneticen Feldes
 | unt | 
|
Venn ein unt dizelbe Funktsion f(t,r)=f'(t',r') aus tsvei Inertsialzüstemen beobaxtet vird, gilt für di Apleitungen
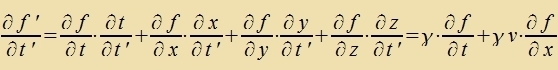
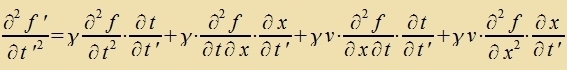 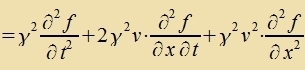
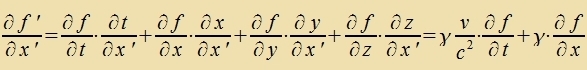
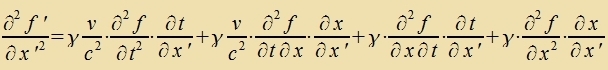 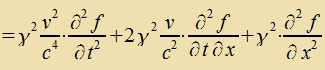
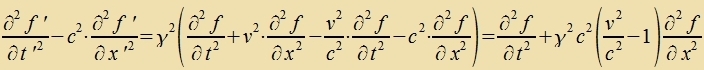 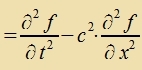
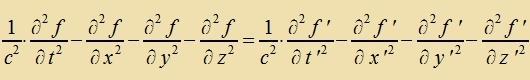
|
|
|
| Venn für eine Funktsion f(t,x) gilt | 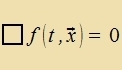 | , | dan gilt für dize Funktsion inn jedem Inertsialzüstem | 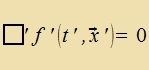
|
Eine Velle mit der Lixtgecvindigkeit c ((22) Kap. XVIII) vird inn allen Inertsialzüstemen als Velle mit der
Lixtgecvindigkeit c beobaxtet, es ändert zix aber durx den Doppler-Effekt di Frekvents f unt vegen c=λ∙f entcprexxend di Vellenlänge.
Der Firerort eines Ereignisses inn der Raum-Tseit kann inn untercidlixxer Veize dargectellt verden, nixt nur durx ko- unt kontravariante Firervektoren. Eine
Möglixkeit ist, di nullte Komponente imaginär tsu creiben: (ict, r). Di Firernorm ist dan das Kvadrat -c²t²+r².
Veiterfürend ist eine andere Darctellung, bei der aus dem Firerort (ct,x) eine hermitece 2X2-Matriks gebildet vird, deren Determinante gleix der Firernorm
ist (zihe Anhang: Lie-Gruppen.).
| | |
| A | | |
|