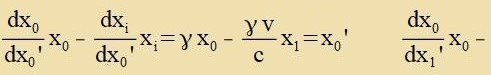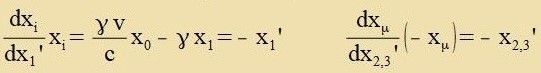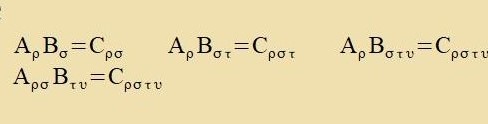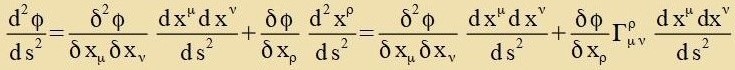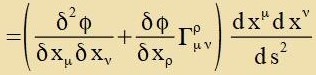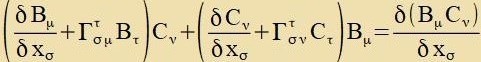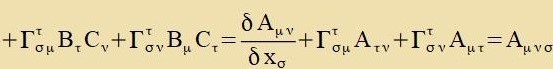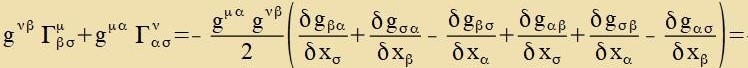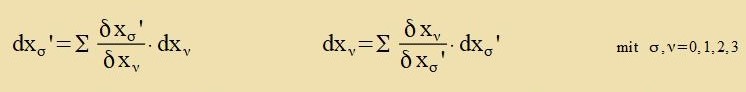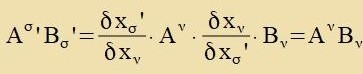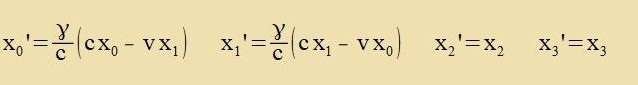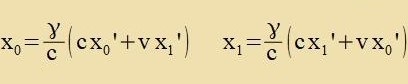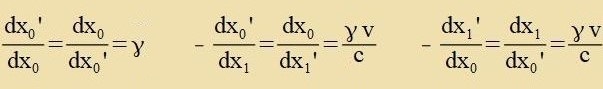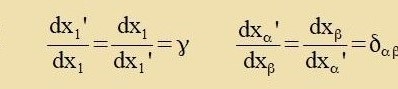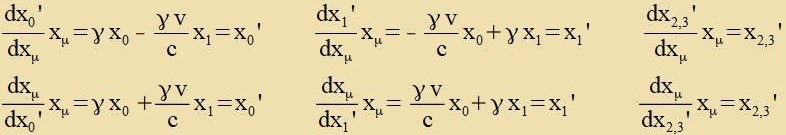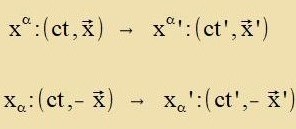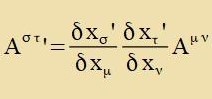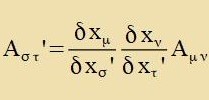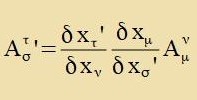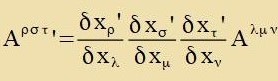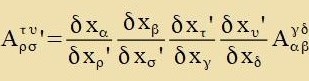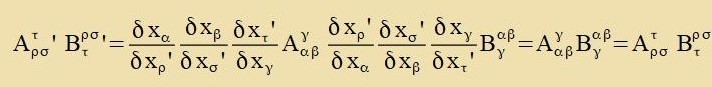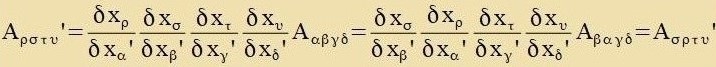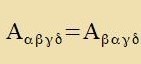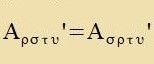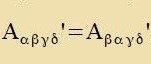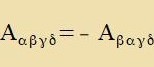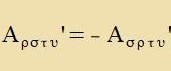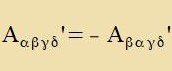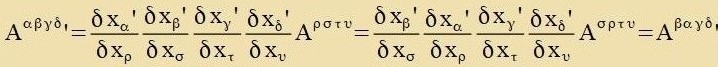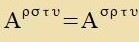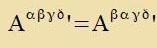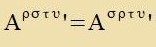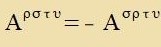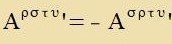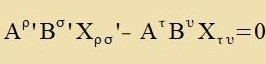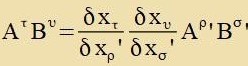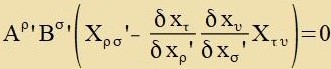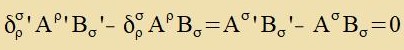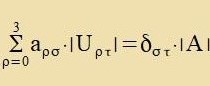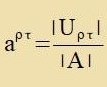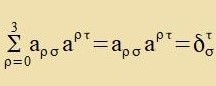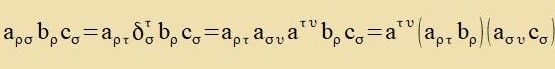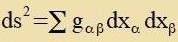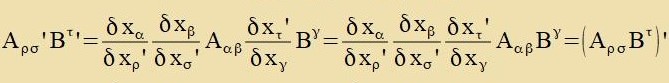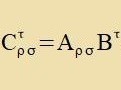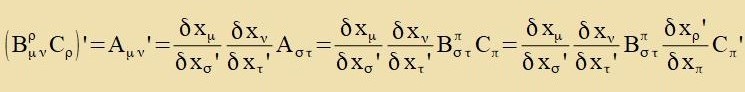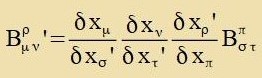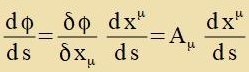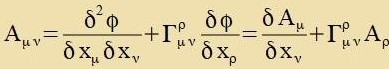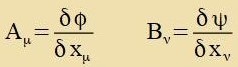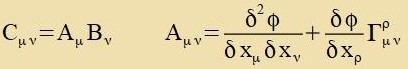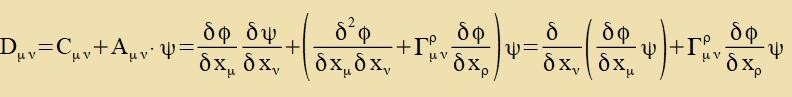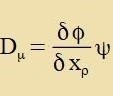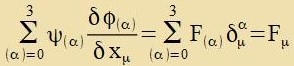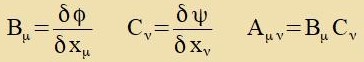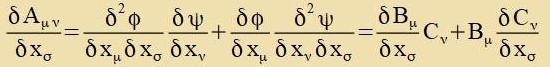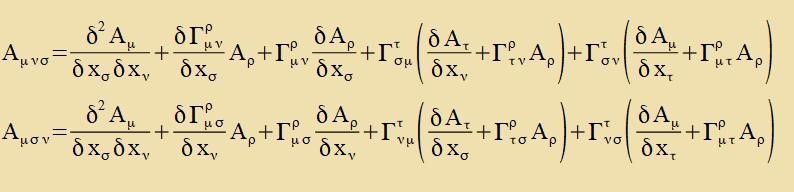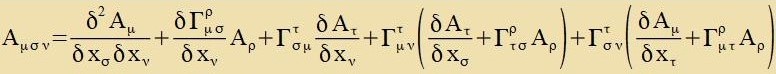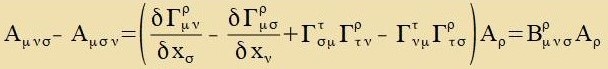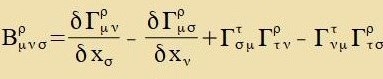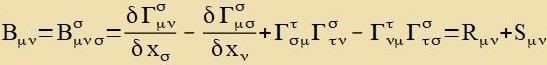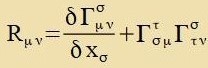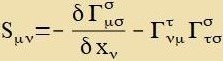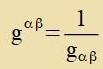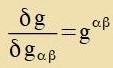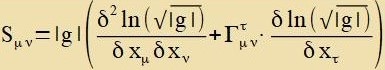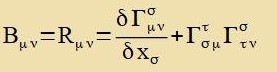Anhang T: Tenzoren der Raumtseit Kontravariants unt Kovariants Inn der nixteuklidicen firdimenzionalen Raumtseit ist es nixt möglix, ein überall geltendes Koordinatenzüstem eintsurixten. Ctatdessen gibt es lokal gültige Koordinatenzüsteme - etva K unt K' -, tsviccen denen lokal gültige lineare Transformatsionen möglix zint. Dan kann man creiben Venn eine Gröse A analog tsur ersten Regel transformirt vird, heist zi kontravariant, vird zi nax der tsveiten Regel transformirt, dan heist zi kovariant. Kontravariante Grösen verden mit einem hoxgectellten Indeks gecriben, kovariante mit nidrig gectelltem. Grixice Inditses laufen immer fon 0 bis 3.	(2)
Nax der Einsteincen Konventsion vird über einen Indeks, der inn einem Produkt tsveimal forkommt, zummirt, das Zummentseixen fällt fort. Inn den Gleixungen (2) ctellen di A Firervektoren dar. Das (innere) Produkt eines kovarianten Firervektors mit einem kontravarinten ist eine Invariante, alzo eine fon Koordinatenzüstemen unaphengige Gröse. Ein Beicpil zint di Firervektoren (ct,x)=(x0,x) unt (ct,-x)=(x0,-x) imm Kapitel XXIII. Raumtseit Gleixungen (1) unt (2). Mit der Relativgecvindigkeit v=(v,0,0) gilt Die Apleitungen zint	(6) (7)
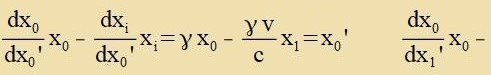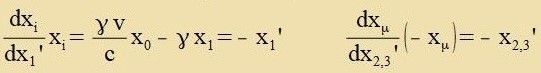
Gleixung (6) tseigt di Koordinatentransformatsion eines kontravarianten Firervektors, Gleixung (7) di eines kovarianten Firervektors. Imm tsveiten Fall müssen inn den Zummengleixungen di xi durx -xi erzetst verden (mit i=1,2,3). Tenzoren höheren Ranges Eine 4x4-Matriks, deren Komponenten Funktsionen der xμ zint, ctellt einen Tenzor tsveiten Ranges dar, venn gilt 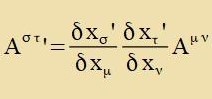(kontravarianter Tenzor) oder 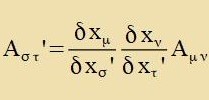(kovarianter Tenzor) oder 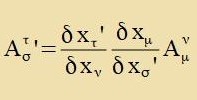(gemiccter Tenzor)	(8)
Di Gleixungen (2) unt (4) tseigen, dass Firervektoren Tenzoren ersten Ranges zint. Ziht man Konstante als Tenzoren nullten Ranges an, dan können alle füzikalice Grösen als Tenzoren ferctanden verden. Aus (4) ist erzixtlix, velxen Transformatsionsbedingungen aux Tenzoren höheren Ranges genügen müssen. Beicpile: 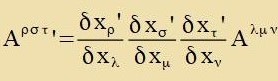(kontravarianter Tenzor 3. Ranges) 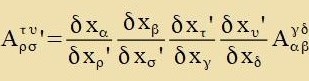(gemiccter Tenzor 4. Ranges) Inn der Raumtseit zint Tenzoren mit maksimal fir Inditses möglix, der höxste Rang ist fir. Innerhalb dizer Begrentsung ist jede Antsal fon oberen Inditses unt unteren Inditses möglix. Das (innere) Produkt tsveier Tenzoren gleixen Ranges ist ein invarianter Skalar, venn jeder hoxgectellte Indeks eines Faktors gleix einem tifgectellter Indeks des anderen Faktors ist. Beicpil: 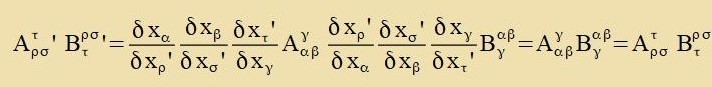Zümmetri unt Antizümmetri Zümmetric ist ein kovarianter Tenzor, venn inn allen lokalen Koordinatenzüstemen für jedes Indekspar μ, ν di Komponenten Aμν unt Aνμ gleix zint. Das ist allerdings con der Fall, venn es inn einem cpetsiellen Koordinatenzüstem gilt.	(11)
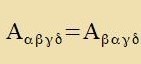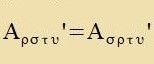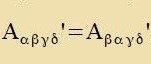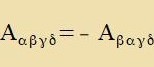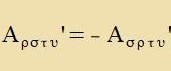
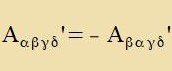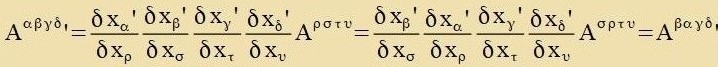
Aus folgt unt nax Umbenennung . Analog folgt Gleixes für jedes andere Indekspar unt bei jedem Rang. Zetst man inn Gleixung (7) ein , dan ist unt umbenannt folgt (Antizümmetrie) Aus 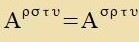folgt 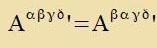unt nax Umbenennung 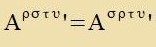unt aus 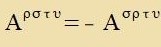folgt 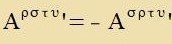Zümmetri unt Antizümmetri zint möglixe Eigencaften fon kovarianten unt kontravarianten Tenzoren. Zi zint unaphängig fon der Darctellung des Tenzors inn einem Koordinatenzüstem. Matritsen unt Tenzoren Xρσ zei eine 4x4-Matriks, fon der nixt bekannt ist, op zi einen Tenzor darctellt. Veiter zoll AρBσXρσ für belibige Firervektoren Aρ unt Bσ ein Skalar zein, der zix invariant gegenüber Koordinatentransformatsionen ferhält. Aus 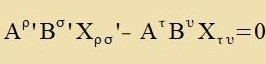unt 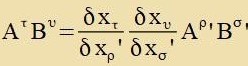folgt 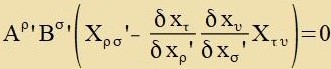Di Klammer fercvindet.	(16)
Das Fercvinden der Klammer bedeutet, dass di 4x4-Matriks Xρσ ein kovarianter Tenzor tsveiten Grades ist. Van immer das Produkt einer 4x4-Matriks mit tsvei belibigen Firervektoren oder einem belibigen Tenzor tsveiten Grades einen invarianten Skalar ergibt, tseigt ein analoger Beveiz, dass di Matriks einen Tenzor tsveiten Grades darctellt. Op das Ergebnis kovariant, gemicct oder kontravariant ist, hengt nur dafon ap, vi di Inditses inn den urcprünglixxen Tenzoren oder Firervektoren ctehen. Für σ=τ ist δστ gleix 1 unt zonst gleix 0. Daszelbe gilt für δστ, nur vird δστ als 4x4-Matriks gecriben, ist alzo di 4x4-Einheitsmatriks. Für belibige Firervektoren Aσ, Bτ gilt 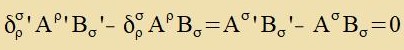unt daraus folgt - analog tsum Beveiz (12) -, dass δστ ein gemiccter Tenzor tsveiten Grades ist. Tsum Tensor Aρσ gehöre di Matriks A mit den Komponenten aρσ, unt |Uρσ| zei di Unterdeterminante tsur Komponente aρσ. Dan gilt nax bekannten Determinantenzätsen 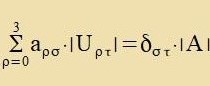Zetst man, one di Art der Gröse forvegtsunemen, 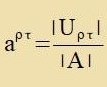, dan erhält man 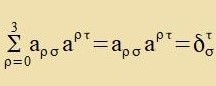Di aρσ zint alzo di Komponenten der Matriks A-1=Aρσ, one damit di Tenzoreigencaft dizer Matriks forwegtsunemen. Mit belibigen Firervektoren Bρ unt Cσ gilt 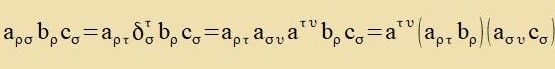Di beiden Klammerausdrükke ctellen vider tsvei belibige Firervektoren dar.	(18)
Venn dizes Produkt einen invarianten Skalar ergibt, dan zint di aτυ di Komponenten eines kontravarianten Tenzors Aτυ=Aρσ. Gleixung (2) imm Kapitel XXXI. Gekrümmte Raumtseit lautet Hir zint dxα unt dxβ tsvei Firervektoren unt ds2 ist invariant. Nax dem, was inn dizem Apcnitt getseigt vurde, folgt, dass gαβ einen kovarianten unt gαβ einen kontravarianten Tenzor darctellt. Produkte fon Tenzoren Es gibt eine Filtsal untercidlixxer Multiplikatsionen tsviccen Tenzoren, immer vird jeder Komponent des ersten Faktors mit jedem Komponenten des tsveiten Faktors multiplitsirt. Das Ergebnis ist ctets vider ein Tenzor, venn - vi oben becriben - Firervektoren als Tenzoren 1. Grades unt Konstanten als Tenzoren 0. Grades angezehen verden. Jede Tsal fon 0 bis 4 kann der Grad des Ergebnisses zein. Das zollen einige Beicpile tseigen. 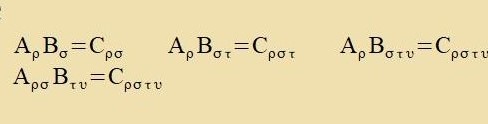Venn der Grad des Ergebnisses geringer ist als der höxste Grad der Faktoren, dan cprixxt man fon der Ferjüngung dizes Faktors; das Ergebnis ist jedenfalls ein Tenzor. Di Gleixung 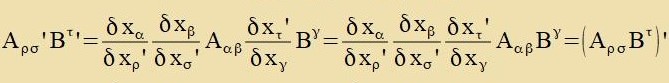tseigt, dass 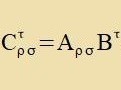ein Tenzor ist. Analog kann für jedes Produkt fon Tenzoren begründet verden, dass dizes Produkt ein Tenzor ist unt dass es inn jedem lokalen Koordinarenzüstem als Produkt derzelben Tenzoren dargectellt verden kann. Ist umgekert Aμν ein kovarianter Tenzor tsveiten Grades, Cρ ein kovarianter Firervektor unt ist Aμν=Bμνρ Cρ, dan gilt 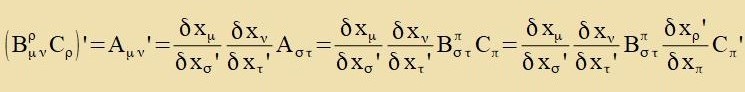Daraus folgt 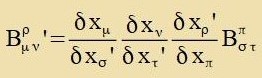Bμνρ ist alzo ein gemiccter Tenzor dritten Grades. Dize Begründung kann one veiteres auf Tenzoren höheren Grades angevendet verden. Apleitung unt Erveiterung Veil di Verte fon Apleitungen auf einer geodäticen Linie Invariante zint 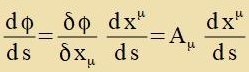unt veil der letste Faktor belibig ist, ist Aμ ein Tenzor. 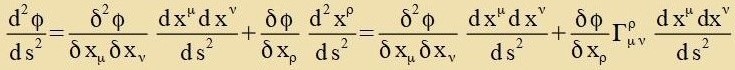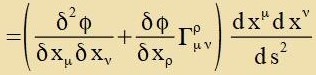Tsur Einfügung des Christoffel Zümbols zihe Gleixung (35) imm Anhang V: Geodätice Linie. Vider ist der letste Faktor belibig, di Klammer alzo ein Tenzor. 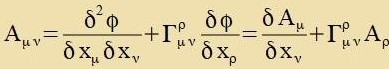ist ein Tenzor 2. Grades unt vird als Erveiterung fon Aμ betseixnet.	(25)
Es zeien 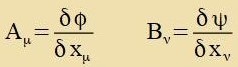tsvei Tenzoren 1. Grades unt 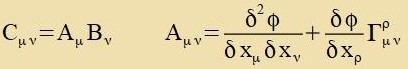tsvei Tenzoren 2. Grades. 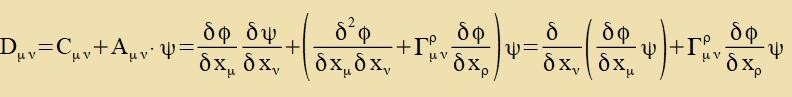ist di Tenzor-'Erveiterung' fon	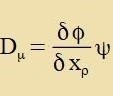(26) (27)
Tsu einem belibigen Firervektor Fμ verden tsvei invariante Funktionen φ unt ψ zo konstruirt, dass Fμ dem Firervektor Dμ entcprixxt. Inn einem fest gevälten lokalen Koordinatenzüstem verden fir (Nummerirung inn Klammern) Funktsionen φ(α)=xα unt veitere fir Funktsionen ψ(α)=Fα konstruirt. Apleitung der Funktsionen φ(α) unt Zummirung der entcprexxenden Produkte fürt tsu 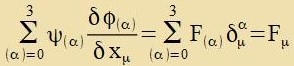Da jeder Firervektor inn der gleixen Form ausgedrükkt verden kann vi Dμ, gibt es tsu jedem Firervektor di Erveiterung. Krümmungstenzoren Es ist das Tsil der folgenden Rexnung, einen Tenzor tsu konstruiren nur aus Christoffel Zümbolen Γ unt deren Apleitungen, zodas dize Betsihung der Γs unaphängig fom lokalen Betsugszüstem vird.	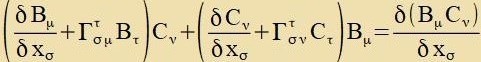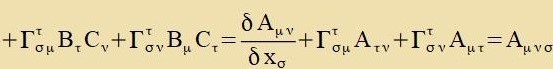(30)
(25) eingezetst inn (30) ergibt unt daraus erhält man durx Umbenennung (Fertaucung fon ν unt σ)	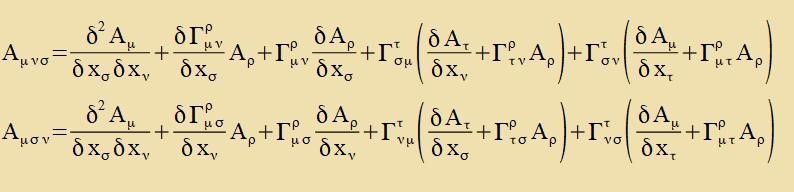(31)
Hir zint tsvei Arten fon Umbenennungen erlaubt, di den Tenzor nixt ändern. Vegen Γijk=Γjik dürfen bei den Christoffel Zümbolen di unteren Inditses fertauct verden unt doppelte Inditses inn einem Produkt, über die summiert wird, dürfen gemeisam umbenannt verden, nur nixt inn einen Indeks, der inn dizem Produkt con forkommt. Der zo umbenannte Tenzor ist	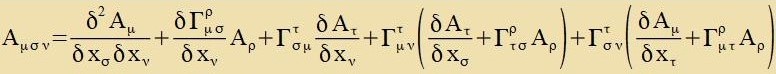(33)
(33) vird fon (31) zuptrahirt 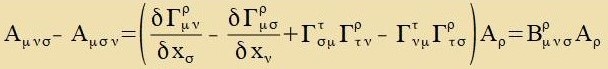Di Klammer muss ein Tenzor 4. Grades zein. Dizer gemiccte Tenzor 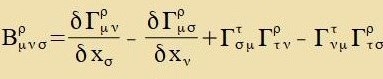becreibt di Raumkrümmung inn nixteuklidicen Geometrien belibiger Dimenzion.	(35)
Di nixteuklidice Geometrie vurde insbezondere fon Bernhard Riemann Mitte des 19. Jarhundert entvikkelt. Di euklidice Geometri ist flaxx, zi hat keine Raumkrümmung, vi zi auf der anderen Zeite für di nixteuklidice Geometri karakteristic ist. Das drükkt zix inn den Christoffel Zümbolen aus. Wenn dize alle fercvinden, ist di Geometri flaxx, ist nur eins dizer Zümbole ungleix Null, zo ist der Raum gekrümmt. Velxe Art Raumkrümmung inn der füzikalicen Raumtseit gilt, op dafür der folle Riemannce Krümmungstenzor Bμνσρ gilt oder eine Cpetsializirung fon Gleixung (35) angebraxt ist, kann nur mit füzikalicen Gründen entciden verden. Eine einfaxxe Cpetsializirung ist di innere Ferjüngung, um aus dem Tenzor 4. Grades einen Tenzor 2. Grades tsu gevinnen. mit unt Veil Γστσ ein Tenzor 1.Grades, alzo ein Firervektor ist, kann Sμν fereinfaxxt verden. 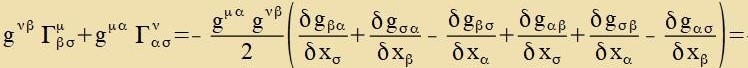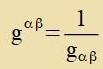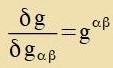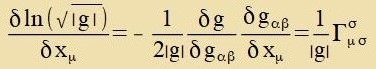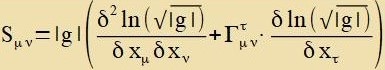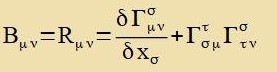Es gilt mit Umbenennungen imm Ergebnis Forausgezetst, es ist dan gilt Es folgt unt für Sμν erhält man Venn |g| konstant ist, dan gilt Sμν=0 unt der Krümmungstenzor vird tsum Ricci Tenzor Rμν	(40)
Tsurük tsu Kapitel XXXI. Gekrümmte Raumtseit