Inn einem einfaxx tsuzammenhengenden Gebit G des Raumes R_n zei K_n di Menge aller tsveimal ctetig differentsirbaren Kurven x(t), di alle den Anfangspunkt x_A=x(t_A) unt den Endpunkt x_B=x(t_B) haben. Di Variable t ist der Parameter für den Durxlauf der Kurven - t muss hir nixt als Tseit ferctanden verden. Di Apleitung fon x(t) nax t, di durx einen Punkt gekentseixnet vird, ist nax der Forauszetsung für di x(t) mindestens einmal ctetig differentsirbar. Veiter zei eine Funktsion g(t,u,v) gegeben, di inn G belibig oft nax allen Komponenten fon u unt v differentsirbar ist.

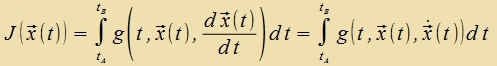ist ein Funktsional der Funktsion g(t,u,v), das aphengig ist fon der Kurve x(t) aus Kn.

(1)

Es zoll eine notvendige Bedingung hergeleitet verden dafür, dass J(x(t)) minimal ist gegenüber J(y(t)) für benaxbarten Kurven y(t) aus K_n.

Es zei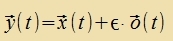 mit 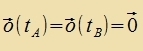Veil y(t) tsveimal ctetig differentsirbar ist, gilt das Gleixe für o(t). Imm übrigen ist o(t) belibig, zodas jedes y(t) aus Kn dargectellt verden kann.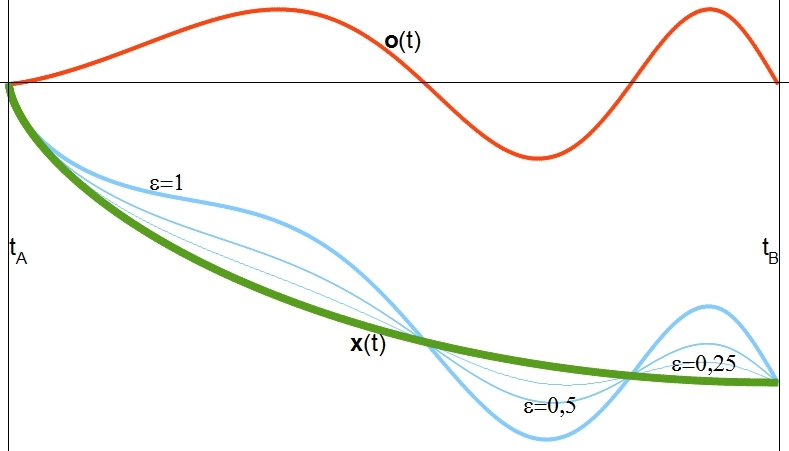

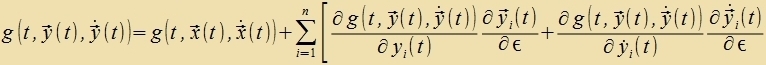
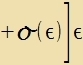
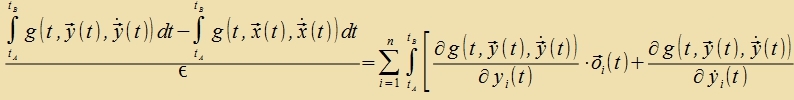
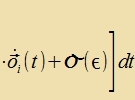
Der Integrand des Funktsionals vird inn eine Reihe nax Potentsen fon ε entvikkelt. Es ist dabei unnötig, di Funktsion g(t,u,v) partsiell nax t tsu differentsiren, da dt/dε=0 ist. Glider höherer als erster Ordnung verden inn o(ε)∙ε tsuzammengefasst.





Venn ε gegen 0 geht, dan fercvindet o(ε), y(t) geht über inn x(t) unt der Differentsialkvotsient vird tsur Apleitung des Funktsionals (A1) an der Ctelle x(t). Eine notvendige Bedingung dafür, dass das Funktsional über di Kurve x(t) minimal ist gegenüber den näxst benaxbarten Raumkurven aus K, ist, dass dize Apleitung vercvindet.

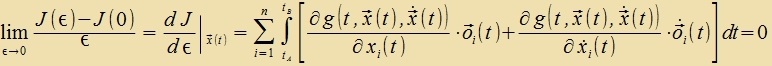(5)

Durx partsielle Integratsion erreixt man, dass o_i(t) ausgeklammert verden kann, der hox geleitete Ausdrukk fercvindet, veil o_i(t_A)=o_i(t_B)=0 ist.

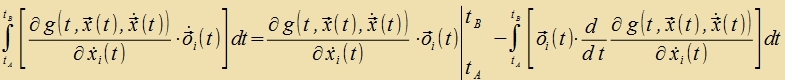
Tsviccenergebnis:

Venn das Funktsional (1) minimal ist, dan gilt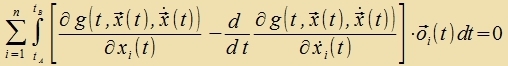

(7)

Es vird nun tsuzätslix forausgezetst, dass es für di Kurven x(t) aus K_n keine Tsvangsbedingungen gibt, dass alzo di x_i(t) unaphengig fon einander zint. Dan gibt es aux keine über di Definitsion hinausgehenden Becränkungen für di Kurven o(t), zi können frei ausgevält verden, um di Bedingung (A7) tsu fereinfaxxen. Zint etva alle o_i(t) gleix Null für i≠k, dan bleibt fon der Zumme nur der Zummand für i=k übrig. Das gilt für jedes k=1,...n, zodas di Zumme inn di n eintselnen Zummanden tserfällt.

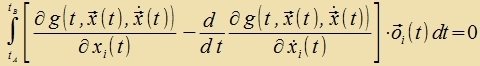für i fon 1 bis n.

Väre di Funktsion inn der ekkigen Klammer für ein t mit t_A ≤ t ≤ t_B ungleix 0, dan gäbe es für dize ctetige Funktsion ein apgeclossenes Interall, in dem zi ungleix null väre, one das Fortseixen tsu vekseln. o(t) vird nun zo gevält, dass es inn dizem Intervall pozitiv, zonst aber überall Null ist. Das Integral väre dan ungleix 0. Es ist alzo nixt möglix, dass di ekkige Klammer imm Intervall t_A ≤ t ≤ t_B irgendvo nixt fercvindet. Daraus folgen di Euler-Lagrange-Gleixungen für i=1 bis n:

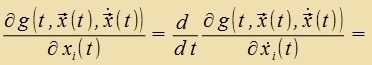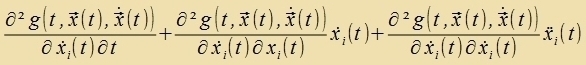(9)

Imm zer häufigen Fall, dass der Integrand inn (1) nixt eksplitsit fon t aphengt, lassen zix di Gleixungen (9) fereinfaxxen.

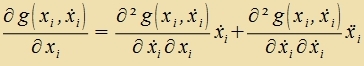(10)

Veiter gilt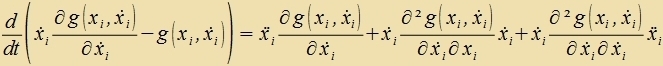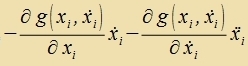

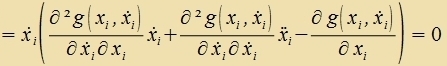Der letste Critt folgt aus (10). Damit erhält man als notvendige Bedingung dafür, dass das Funktsional (1) minimal vird, di zogenannte Beltrami Identität

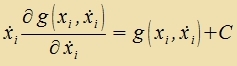mit i=1 bis f unt konstanten C.

(13)

Forausgezetst ist, dass di x_i(t) tsveimal stetig differentsirbar unt fon einander unaphengig zint. Auserdem muss g(x_i(t),dx_i(t)/dt) stetig differentsirbar zein unt darf nixt eksplitsit fon t aphengen.


Dize matematicen Herleitungen zint frei fon irgendvelxen füzikalicen Inhalten. Veder ist di Antsal f der Komponenten x_i festgelegt, nox ire Art. Veder für den Kurvenparameter t nox für den Integranden, di Funktsion g, ist eine füzikalice Bedeutung gegeben. Erst bei der Anvendung muss geklärt verden, für velxe füzikalicen Grösen di Funktsion g, der Parameter t unt di x_i ctehen.

Bei den häufigsten Anvendungen inn der Füzik ist der Kurvenparameter t di Tseit unt der Integrand eine Energi, di als Lagrange-Funktsion L gecriben vird. Da aber inn den zeltensten Fällen di Bankurve inn kartezicen Koordinaten ausgedrükkt vird, zint di Argumente inn der Lagrange-Funktsion 'ferallgemeinerte Koordinaten' q, di zo gevält verden, dass zi fon einander unaphengig zint. Ire Tsal f ist der Freiheitsgrad des Züstems. Das Funktsional ergibt eine Virkung
S = ∫ W dt, unt venn dize Virkung nax dem d'Alambertcen Printsip ekstremal verden zoll, folgen aus den Euler-Lagrange-Gleixungen (9) di Lagrange-Gleixungen der Füzik unt als Zonderfall di einfaxxere Beltrami Identität (10).

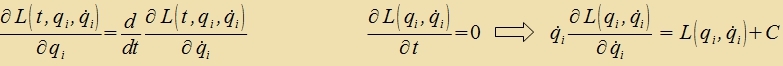für i=1,....f

(14)

Matematic gezehen erfüllen Lözungen fon (4) nur eine notvendige Bedingung. Op das aux hinreixend ist, ist für di Füzik venig interessant. Vixtig ist nur, op zolxe Lözungen eine füzikalic reale Bedeutung haben.

Tsurük tsu Kapitel VI. Analütice Mexanik

Variatsionsrexnung für Felder

Das Funktsional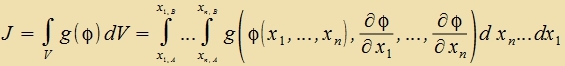

zoll minimal verden.

(15)

Das n-dimenzionale Volumen V, über das integrirt vird, ist durx di Integratsionsgrentsen festgelegt. Eine Variatsion der x_i imm Volumen V bevirkt keine Änderung. Daher brauxt nur di Aphengigkeit der Funktsion g fon φ unt, venn g inn erster Näherung entvikkelt vird, di Abhengigkeit fon den partsiellen Apleitungen berükzixtigt verden. Tsur Variatsion der Funktsion φ(x₁, ... ,x_n) vird eine Funktsion ε∙o(x₁, ... ,x_n) datsu addirt, di auf dem Rand fercvindet.

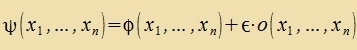
Inn erster Näherung gilt dan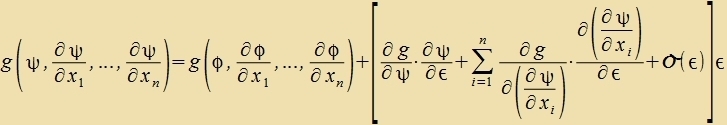
Der Differentsenkvotsient des Funktsionals ist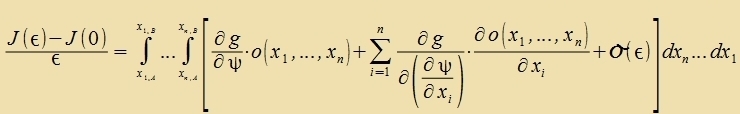

Venn ε gegen Null geht, fercvindet der letste Zummand inn der Klammer, ψ geht gegen φ unt es entcteht di Apleitung des Funktsionals an der Ctelle φ, di gleix Null zein muss, venn das Funktsional für di Funktsion φ ein Minimum annimt.

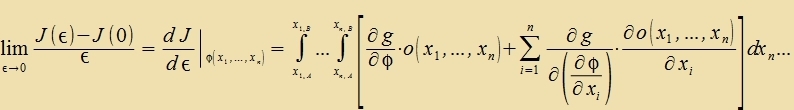
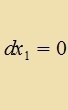
Nax partsieller Integratsion ist das erste Glid gleix Null, veil eine Funktsion auf dem Rand vercvindet.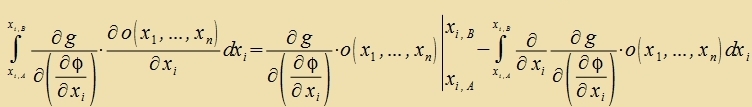

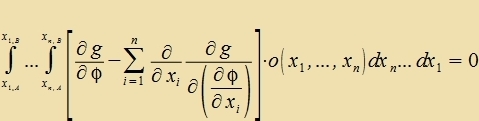Väre der Integrand inn einem Punkt P unt deshalb vegen der Ctetigkeit inn einer Umgebung fon P pozitiv (oder negativ), dan vird o(x1, ... ,xn) zo gevält, dass es inn dizer Umgebung pozitiv unt zonst Null ist. Das Integral väre ungleix Null. Vidercpruxx!

Venn das Funktsional (1) für di Funktsion φ(x1, ... ,xn) minimal ist gegenüber eng benaxbarten Funktsionen, dan gilt di Lagrange-Gleixung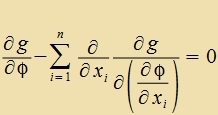

(22)

Mit n=4 unt n4=t erhält man di Lagrange-Gleixung für ein Feld imm dreidimenzionalen Raum.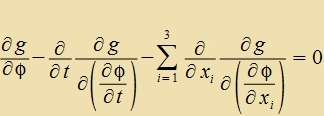

(23)

Geodätice Linie

Inn einem Raum belibiger Dimenzion vird di geodätice Linie bectimmt, indem di Variatsion über das Funktsional S=∫ds gleix Null gezetst vird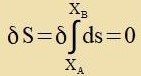
Inn einem firdimenzionalen nixteuklidicen Raum zei das gegenüber dem lokalen Koordinatenzüstem invariante Linienelement gegeben durx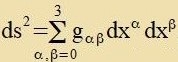

Hir unt imm folgenden zint di x^μ kontravariante Koordinaten. Durx eine Funktsion λ(x_ν) kann eine Car fon Fläxxen bectimmt verden, di di Kurven tsviccen den beiden Punkte X_A unt X_B cneiden. Di Koordinaten x^μ der geodäticen Linie können dan durx λ ausgedrükkt verden unt eine Variatsion fon λ fürt tsu einem Punkt auf einer benaxbarten Kurve. Zo kann aus allen Kurven tsviccen X_A unt X_B dijenige ausgevält verden, für di das Funktsional S=∫ds einen Ekstremvert annimt. Es gilt

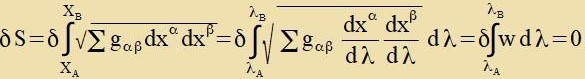Hir ist w definirt durx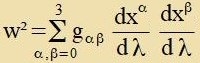

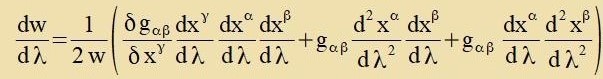
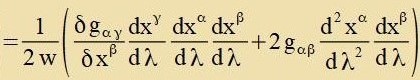
Imm folgenden gilt Einsteins Zummenkonventsion. Danax vird inn Produkten über einen grixicen Indeks, der inn tsvei Faktoren auftrit, fon 0 bis 3 zummirt, das Zummentseixen fällt fort. Um vi inn den beiden forigen Apcnitten di erste Näherung der Funktsion w(λ) tsu bectimmen, vird di Apleitung bectimmt. Di Änderungen nax dem tsveiten Gleixheitstseixen zint als reine Umbenennungen tsulässig.



Damit kann di Apveixung ΔS der raumtseitlixxen Veglänge einer Kurve fon der geodäticen Linie inn erster Näherung angegeben verden. Vider vird vi con oben inn dizem Kapitel einer der beiden Zummanden im Integranden partsiell integrirt.

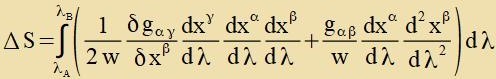
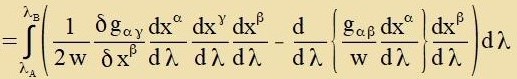
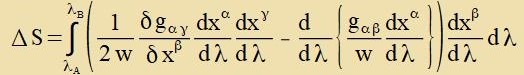Da der letste Faktor belibig ist, folgt, dass di Klammer (...) fercvindet.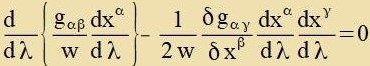

Mit λ=s folgt w²=1 aus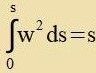

Di Euler-Lagrange-Gleixungen für di geodätice Linie lauten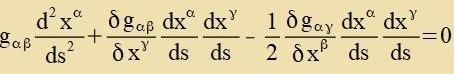

(31)

Es gilt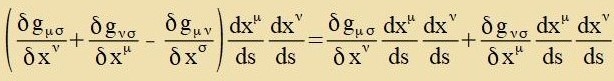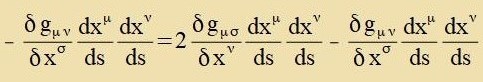

Damit kann Gleixung (31) umgeformt verden tsu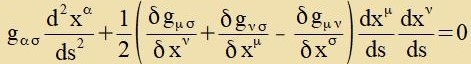

Ist clislix gασ di tsu gασ inverze Matriks, dan gilt

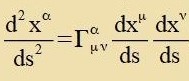mit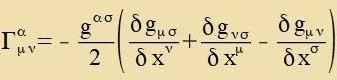

(35)

Dizes Gleixungszüsten gibt di Bedingungen an für eine geodätice Linie inn der nichteuklidicen Geometri, di imm neuntsenten Jarhundert insbezondere fon Riemann unt Christoffel entvikkelt vurde. Di Γ^α_μν zint di Christoffel-Zümbole tsveiter Art.



Tsurük tsu Kapitel XXXI. Gekrümmte Raumtseit