Fundctelle
|
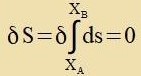
Für di Raumtseit hat Minkowski das Linienelement ds mit
ds2=c2⋅dt2-x2=μαβ⋅dxαdxβ definirt. Hir unt imm folgenden
vird di Einsteince Zummenkonventsion angevendet unt grixice Inditses laufen ctets fon 0 bis 3. Mit dem metricen Tenzor gαβ ctatt
μαβ erhält man
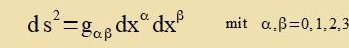 | Das vird eingezetst inn (1) | 
| | (1)
(2)
|
|
| Di gαβ bilden eine 4x4-Matriks | 
| Erzetst man gαβ durx μαβ, zo erhält man | 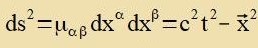
| | (3)
|
|
Damit di Ferformung der Raumtseit durx Gravitatsionsfelder dargectellt verden kann, muss der metrice Tenzor gαβ zix fom Tenzor
μαβ der cpetsiellen Relativitätsteori unterceiden unt ortsaphengig zein. Das clist ein, dass der Untercid tsviccen gαβ
unt μαβ inn veiten Gebiten der Raumtseit gering ist oder azümptotic fercvindet. Dize Nähe tsviccen beiden Tenzoren vird durx einige
Annamen gezixxert, di der cpetsiellen Relativitätsteori entcprexxen:
|
a) di gαβ zint reelle Funktsionen der xα
b) gαβgαβ ist di 4X4-Einheitsmatriks E
c) di Determinante gαβ ist g=-1, alzo eine Konstante
d) venn bei einer Koordinatentransformatsionen aαβ tsviccen lokalen Züstemen |aαβ|=±1 gilt, bleibt Anname c) erhalten
| | (4)
|
|
Füzikalice Grösen, di zix mit dem Ort inn der Raumtseit ändern, zint Invariante, vekseln aber ire Darctellung je nax dem, inn velxem Betsugszüstem zi dargectellt
verden. Di fercidenen Darctellungen gehen bei Koordinatentransformatsionen inn einander über, vobei dize Transformatsionen eine matematice Gruppe bilden, zodas di
Darctellung inn jedem Züstem eindeutig ist. Um inn der nixteuklidicen Geometri Naturgezetse tsu becreiben, reixen Vektoren unt Firervektoren nixt aus, dafür zint
Tenzoren nötig. Matematice Grundlagen tsur Rexnung mit Tenzoren zint becriben inn Anhang T: Tenzoren der Raumtseit. Dort vird
insbezondere imm Apcnitt Matritsen unt Tenzoren getseigt, dass di Matriks G einen kovarianten Tenzor darctellt unt
vi der tsugehörige kontravariante Tenzor tsu bilden ist.
Di Euler-Lagrange-Gleixungen für di Variatsion (2), alzo di Bedingungen für eine geodätice Linie zint hergeleitet imm
Anhang V: Geodätice Linie.
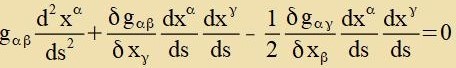
| Inn anderer Formulirung: | 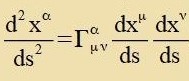 | mit | 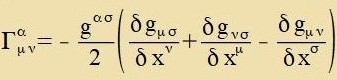 | unt | 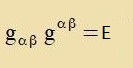
| | (5)
(6)
|
|
Durx die Christoffel Zümbole Γ vird di Virkung einer Raumkrümmung auf di Geodäten dargectellt.
Nax zeiner Relativitätsteori vird di Gravitatsion inn der Raumtseit Einsteins hauptzäxxlixxes Arbeitsfeld. 1908 creibt er inn einem Artikel über
gravitative Rotfercibung unt drei Jare cpäter über Lixtaplenkung durx eine Masse. Inn einem Artikel, den er 1913 gemeinzam mit Marcel Grossmann
feröffentlixt, creibt er, es zei zein Tsil, Poisson's Gleixung Δφ=4πρ durx eine Gleixung der Form
κ⋅Θμν=Γμν tsu ferallgemeinern. Inn dizer Gleixung ist
κ eine Konstante, Θμν der Energi-Impulz-Tenzor (heute meist Tμν gecriben) unt
Γμν ein nox tsu bestimmender Tenzor tsveiter Ordnung vi Θμν, der durx
Differentsialoperationen aus dem metricen Tenzor gμν tsu bilden zei unt dessen Divergents vi di fon
Θμν fercvinden müsse. Inn dizem Artikel zint alle Betsihungen fon (1) bis (6) ervänt, nixt aber irgend ein
Krümmungstenzor. Als Einstein cpäter beginnt, den Riemanncen Krümmungstenzor tsu analüziren, ctellt er fest, dass di Rexnungen vezentlix einfaxxer
verden, venn di Determinante des metricen Tenzors gαβ gleix der Deteminante μαβ der
Minkowski Raumtseit ist. Unter dizer Bedingung ist aux gevärleistet, dass imm Vakuum mit gröser verdender Entfernung fon jeder Masse ein glatter
Übergang fon gαβ tsu μαβ ctatfindet. Einstein ctellt für Räume one Materie
di "einfache Regel" auf, "daß √-g=1" zein zoll, unt dize Regel fürt datsu, dass imm ferjüngten Riemanncen Krümmungtenzor
Bσμνσ
di Hälfte der Zummanden fortfällt. Di fraglixxen Tenzoren zint (zihe Krümmungstenzoren)
Der Ricci Tenzor Rμν vird nixt vi gefordert divergentsfrei zein. Aber imm Vakuum, vo der Energi-Impulz-Tenzor fercvindet, cpilt das
keine Rolle.
| Einsteins Feldgleixungen für das Vakuum zint | 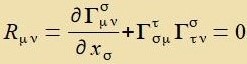 |
| | (8)
|
|
Als Mitte des 19. Jarhunderts geklärt var, velxen Einfluss di gegenzeitige Massenantsihung der Planeten auf ire Banen hat, blib als unerklärter Rest eine
Periheldrehung inn der Ban des Merkur. Mit der Gleixung Rμν=0 berexnete Einstein 1915 näherungsveize di Raumkrümmung in der
Umgebung der Zonne unt tseigte, dass dize Raumkrümmung di Urzaxxe für di Periheldrehung der Merkurban unt für eine Lixtaplenkung am Zonnenrand fon
1,75 Bogenzekunden ist. Bezonders di Bectätigung der Lixtaplenkung durx eine Ekspeditsion tsur Zonnenfinsternis 1919 maxxte Einstein tsu einer veltberümten
Perzönlixkeit. Venige Monate nax Einsteins Näherungsrechnung fand Schwarzschild mit der Schwarzshild-Metrik eine eksakte Lözung der Gleixung (8) unt berexnete
di genauen Verte für di Periheldrehung unt di Lixtaplenkung (zihe Kapitel XXXII Metriken der Raumtseit). Durx den Erfolg der
Vakuumlözungen var bevizen, dass der Ricci Tenzor di Raumkrümmung inn der Umgebung einer Masse rixtig becreibt. Um aus dem Ricci Tenzor einen divergentsfreien
Tenzor tsu bilden, fand Grossmann mithilfe der Bianchi-Identität di geeignete Ergäntsung, zodas nun der Einstein Tenzor
Gμν dem Energi-Impulz-Tenzor Tμν (zihe Kapitel XXIII Raumt-Teit) mit einem
konstanten Faktor κ gleixgezetst verden konnte.
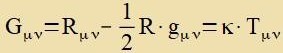 | mit dem Ricci Skalar | 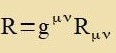
| | (9)
|
|
Der Riemannce Krümmungstenzor Bρμνσ gilt für Räume belibiger Dimenzion,
durx di Cpetsializirung Bρμνσ=Bμν entcteht ein Tenzor, der durx
eine 4X4-Matriks dargestellt verden kann unt damit für firdimenzionale Räume gilt. Di Becneidung des Riemann Tenzors Bμν
auf den Ricci Tenzor Rμν ändert daran nixts unt zo ist Rμν der einfaxxste Tenzor, mit dem di
Raumtseit becriben verden kann. Tsu dizen Tenzoren kann jeveils durx Kontraktsion ein Skalar gebildet verden, der di Ctärke der Krümmung beschreibt.
Väre der Ricci Skalar gleix Null, dann väre di Raumtseit flaxx. Ctatt di Differents tsviccen Rμν unt
κTμν mit dem Ricci Skalar austsugleixen, kann dis aux mit einem aus dem Energi-Impulz-Tenzor gevonnenen Skalar gecehen.
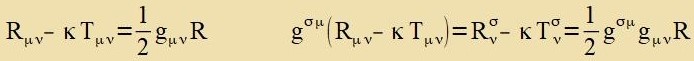
Man kann annemen, dass der metrice Tenzor mit geringen Apveiungen diagonal ist unt di Apveixungen der Diagonalelemente fon der Eins gering zint unt zix gegenzeitig
ausgleixen; denn di Determinante zoll gleix -1 zein. Dan vird di Zumme der Kvadrate gleix 4. Bei der Kontraktsion mit σ=ν entcteht
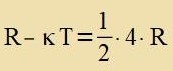 | Eingezetst inn Gleixung (9) ergibt eine tsveite Form der Feldgleixung | 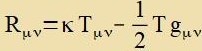
| mit | 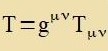
| | (11)
|
|
Di Konstante κ kann mithilfe eines belibigen Beicpils betimmt verden. Di Kvelle des tseitlix kaum feränderlixxen Becleunigundsfeldes inn der
Zonne unt irer Umgebung ist deren Energidixte w=ρ⋅c2. Lässt man tseitlixxe Änderungen beizeite, dan ist
T=w=ρ⋅c2 unt es gilt δgμν/δx0≈0
| Mit i=1,2,3 folgt | 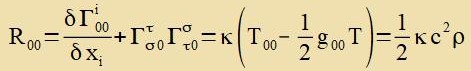 | unt | 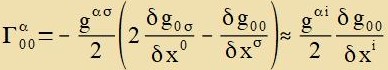
| | (12)
|
|
| Der Parameter s vird inn Gleixung (6) für di geodätice Linie durx di Tseit t erzetst. | 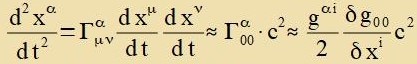
| | Mit α=i unt vegen gii≈1 entcteht eine Vektorgleixung | 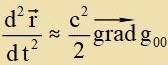
| Das Becleunigungsfeld vird durx den Gradienten fon g00 bectimmt.
| | (13)
(14)
|
|
| Veiter gilt | 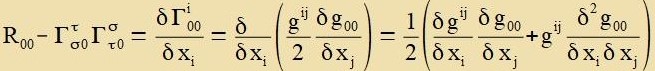
|
Inn der Zonne unt inn irer Umgebung ist di Apveixung fon der euklidicen Geometri gering. Di Christoffelzümbole, di dize Apveixung becreiben, zint inn der
Zonnenumgebung daher kleine Grösen unt Produkte tsveier Christoffelzümbole nox kleiner. Dagegen können Apleitungen nax den xi,
insbezondere di tsveite Apleitung grösere Verte annemen. Damit gilt für R00 näherungsveize:
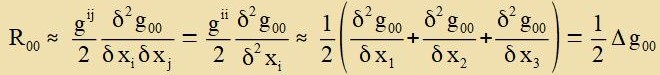 | unt mit Gleixung (12a) folgt | 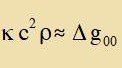
|
| Integratsion über di Zonnenkugel lifert | 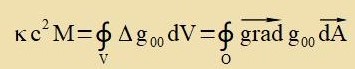 | M und V zint Masse unt Volumen der Zonne.
|
Imm letsten Integral vird über di Oberfläxxe O einer belibige Kugel mit dem Radius r gröser als der Zonnenradius integrirt. Vegen der Kugelzümmetri
zint Gradient unt Fläxxenelement dA parallel unt der Betrag des Gradienten auf der Kugel konstant. Mit Gleixung (14) erhält man:
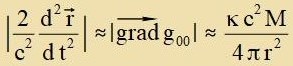 | Vi beim Newtoncen Gravitatsiongezets ist d2r/dt2 proportsional tsu
M/r2 | 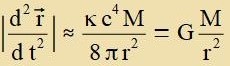
|
Einsteins Feldgleixungen (9) enthalten das Newtonce Gravitatsionsgezets als fereinfaxxte Näherung.
| Der Fergleix ergibt | 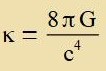 | unt | 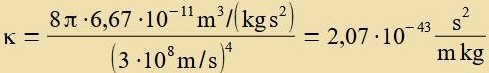
|
Veil durx di Allgemeine Relativitätsteori der apzolute Raum nixt mer als Träger aller füzikalicen Forgänge inn Frage kam, zuxte Einstein nax einem
neuen Modell für das Veltall. Als nax zeinen Rexnungen dizes Model nixt ctabil var, vas der allgemeinen Forctellung vidercprax, fügte er eine kosmologice Konstante
Λ inn di Feldgleixungen ein.
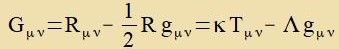 | (20)
|
|
Ein Modell für das Veltall var Gegenctand häufiger Diskussionen tsviccen Einstein unt Willem de Sitter. Einsteins Leitide var lange Tseit das Machce Printsip, nax
dem di Urzaxxe der Trägheit fon Körpern di Massenferteilung imm Veltall zei, värend de Sitter das Machce Printsip für eine rein filizofice Ide hilt. 1917 entvikkelte
de Sitter ein Model mit Tμν=0, inn dem file Velten möglix zint (zihe Kapitel XXXVII Alternativen.).
Di Gecixte der kosmologicen Konstante Λ ist zer vekselhaft. Tseitveize vurde zi gectrixxen, dan vider eingezetst unt ebenzo vekselhaft var ire Bedeutung. Λ cpilt heute
vider eine Rolle bei dem Ferzux, mit Gleixung (20) di tseitlixxe Entvikklung des Kosmos tsu becreiben, unt auf Λ gründet aux de Sitter zein Model.
Als di ART entctand, gab es für eine Überprüfung nur di Periheldrehung des Merkur unt di Lixtaplenkung am Zonnenrand. Di ART vurde veiter entvikkelt,
es gab aber lange nixts Neues, auf das die Teori angevendet verden konnte. Erst inn neuerer Tseit haben di Beobaxtungen fon Cvartsen Löxxern unt fon
Gravitatsionvellen eindeutig bectätigt, dass di ART Raum unt Tseit rixtig als gekrümmte Raumtseit becreibt.
|





