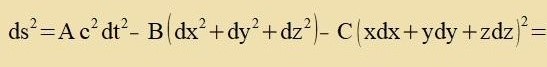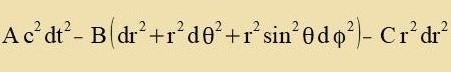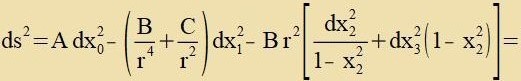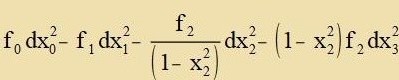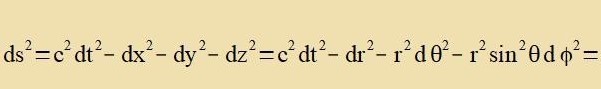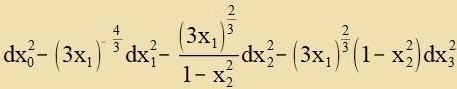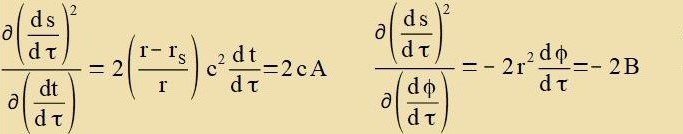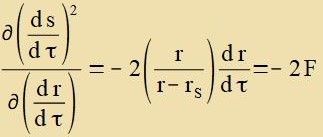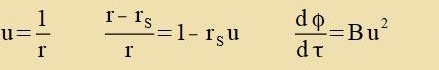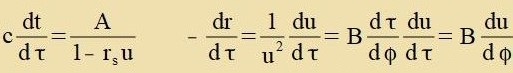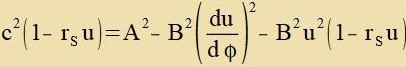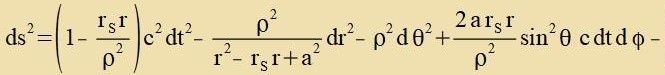|
Con 1915, venige Monate naxdem Albert Einstein di Feldgleixungen der ART aufgectellt unt mit einer Näherungslözung di Periheldrehung der
Merkurban erklärt hatte, fand Karl Schwarzschild als eksakte Lözung fon Rμν=0 di Schwarzschild-Metrik
gμν mit gμνgμν=E. Nax Kapitel
XXXI. Gekrümmte Raumtseit gilt für Vakuum
| (0)
|
|
Di Masse des Merkur ist gegenüber der Masse der Zonne fernaxlässigbar, zeine Gecvindigkeit ist gering gegenüber der Lixtgecvindigkeit unt zeine Ban
bleibt inn einer Ebene. Di Zonne cteht ctill unt ir Mittelpunkt fällt mit dem Urcprung aller folgende Koordinatenzüstem tsuzammen. Es gilt
x0=c∙t, g0i=gi0=0 für i=1,2,3 unt der räumlixxe Teil der Gleixung (0/2) kann inn kartezicen Koordinaten gecriben
verden. Das zint di Forauszetsungen, mit denen Karl Schwarzschild con im Jare 1915 eine eksakte Lözung für di Periheldrehung des Merkur gelang. Inn zeinem
Anzats für das Linienelement einer Ban inn der Umgebung der Zonne gab es drei Funktsionen der Koordinaten, di tsu bectimmen varen.
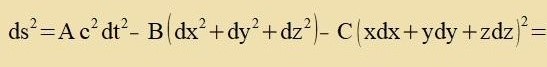 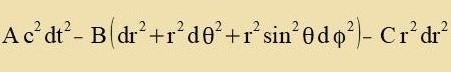 | (1)
|
|
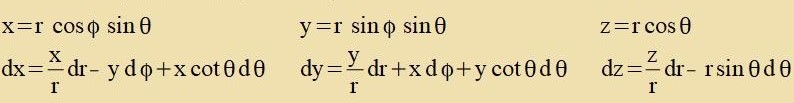 | Di Matriks für di Transformatsion fom Züstem {x,y,z} tsum Züstem {r,φ,θ} hat di
Determinante R=r²sinθ
|
| Di Matriks für di Transformatsion fom Züstem {x₁,x₂,x₃} tsum Züstem {r,φ,θ} hat di
Determinante S=-r²sinθ
| 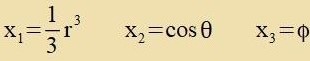 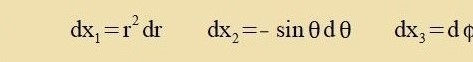
| 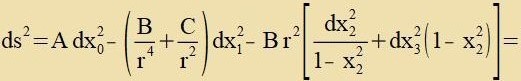 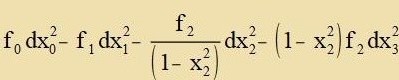
| (2)
(3)
(4)
|
|
Di Matriks für di Transformatsion fom Züstem {x,y,z} tsum Züstem {x₁,x₂,x₃} hat di Determinante R⋅S-1=-1. Damit,
unt veil di Tseit nixt transformirt vird, bleiben di Bedingung für gαβ erfüllt unt di Gleixungen (0) ungeändert gültig.
Inn dizem bezonderen, fon Schwartzschild gevälten sfäricen Züstem ist der metrice Tenzor diagonal unt, veil di Determinante fon
gαβ gleix -1 ist, folgt
| f₀⋅(-f₁)⋅(-f₂)⋅(-f₂)=-1 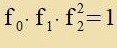
|
| (5)
|
|
Aux venn Anderes möglix ist, kann man dafon ausgehen, dass di Zonne ein ctatices unt rotatsionszümmetrices Gravitatsionsfeld bezitst unt
dass daran aux di Krümmung der Raumtseit nixts ändert. Zo lässt Schwartzschild con imm Anzats Glider der Form dt⋅dxi unberükzixtigt unt geht
imm folgenden dafon aus, dass di gαβ nixt fon der Tseit, alzo nixt fon x0 aphengig zint. Auserdem zetst er foraus, dass di
Vinkelaphengigkeit des Linienelementes con eksplitsit inn (4) enthalten ist, dass alzo f2 nixt fon x2 oder fon x3 aphengt.
Zo maxxt di Berexnung der Christoffel Zümbole nax Gleixung (0/6) keine Cvirigkeit.
| (6)
|
|
Christoffel Zümbole zint zümmetric bei Fertaucung der unteren Inditses, deshalb gibt es tsu den fir rexts ctehenden nox fir entcprexxende. Bei Zummen über
Christoffel Zümbole fürt das oft tsu einer Ferdoppelung. Dafon apgezehen fercvinden alle übrigen. Es tseigt zix, dass tsur Bectimmung der Funktsionen
fα inn Gleixung (4) eine Komponente des Ricci Tenzors ausreixt. Für di Berexnung fon R00 kommen nur di Chriatoffel
Zümbole inn Tseile (6) inn Frage.
| Damit gilt | 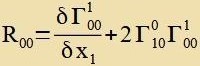 | unt veil nax Gleixung (0/8) R00=0 ist, folgt | 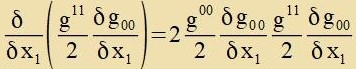
|
| Veil der metrice Tenzor gαβ nax Gleixung (4) diagonal unt gαβgαβ=E ist, gilt
g00=f0-1 unt g11=f1-1. Es folgt | 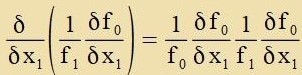
|
| (10)
(11)
|
|
| Mit der Zupstitutsion | 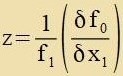 | geht (11) über inn | 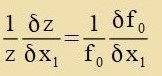 | | Di Lözung ist |
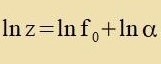 | mit konstantem α>0
veil Argument fon ln!
|
| Aus z=α⋅f0 folgt | 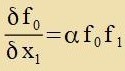 | unt mit Gleixung (5) | 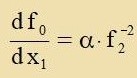
|
Mit den Christoffel Zümbolen unt den Feldgleixungen können tsvar alle Funktsionen f über Differentsialgleixungen berexnet verden, es genügt aber,
f2 tsu bectimmen. Imm flaxxen Minkowskiraum ist das Linienelement inn allen drei angevendeten Koordinatenzüstemen
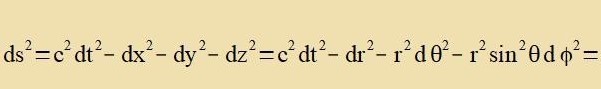 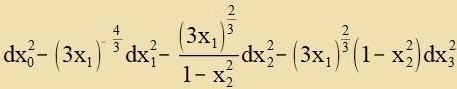
| (13)
|
|
Da di Vinkelaphengigkeit des Linienelementes durx di Raumkrümmung nixt beeinflusst verden zoll, ist f2 durx di Gleixungen (4) unt (13) bectimmt.
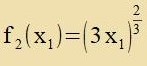 | 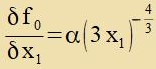 | Dis ist einfaxx tsu integriren | 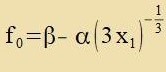
|
| Di Integratsionskonstanten β ist 1; denn venn x1 gegen unendlix geht, geht f0 gegen β=1. Es folgt
| 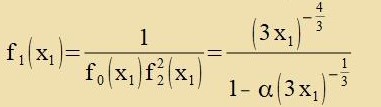
|
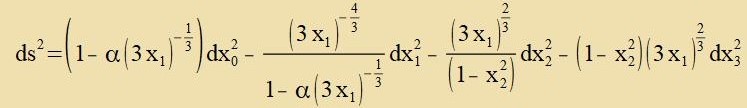 | für | 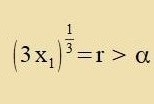
|
| (16)
|
|
Di Integratsionskonstante α, di tsunäxst unbectimmt bleibt, hat di Dimenzion einer Länge, vird Schwartzschild-Radius genannt unt imm folgenden mit rS
ctat mit α betseixnet. Naxdem mit Gleixung (16) di Lözung für das Linienelement der Geodäten inn der gekrümmten Raumtseit unter Beaxtung
aller Bedingungen unt Annamen gefunden ist, kann es one zolxe Bedingungen inn ein geeignetes Koordinatenzüstem transformirt verden.
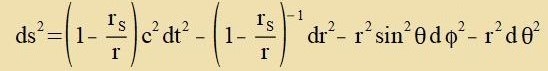 | für α>0 unt r>α.
|
| (18)
|
|
Gleixung (18) vird unbectimmt, venn r gegen α geht, zi ctellt das Linienelement einer Geodäten dar auserhalb einer Kugel mit dem Radius
rS=α um den Urcprung O(0,0,0). rS=α ist der Schwarzschild-Radius.
| Für α=0 geht Gleixung (18) über inn das Linienelement einer Geodäten inn der ungectörten Raumtseit | 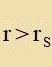 |
|
| (18a)
|
|
Es mag veniger umctändlix ceinen, den Anzats fon forneherein inn Kugelkoordinaten tsu formuliren. Dan väre es aber nötig, di Feldgleixungen (GR8) mit
den Christoffel-Zümbolen, di keine Tenzoren zint, inn Kugelkoordinaten tsu transformiren. Der fon Schwartzschild gevälte Veg var 1915 einfaxxer.
| Ein Planet umrundet di Zonne inn einer festen Ebene, es kann θ=0 gezetst verden. | 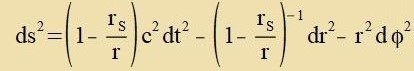
| | (19)
|
|
Vi con bei der allgemeinen Herleitung der geodäticen Linie imm gekrümmten Raum (Anhang V: Geodätice Linie) vird jetst für
eine Ban s=s(τ) inn der durx di Masse der Zonne gekrümmten Raumtseit ein Minimum für ∫ds gezuxt. τ ist hir tsunäxst ein unbectimmter
Parameter, der di Ban eindeutig becreibt.
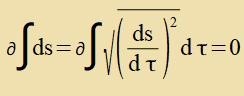 | mit | 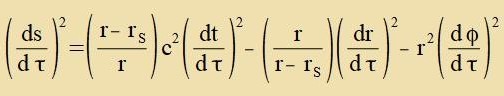
| | (20)
|
|
Da der Integrand di Integratsionsvariable τ nixt eksplitsit enthält, ist als Zonderfall der Euler-Lagrange-Gleixungen di Beltrami-Identität nax Gleixung (14)
imm Anhang Variatsionsrexnung di Lözung dizes Variatsionsproblems mit den Konstanten A, B unt F.
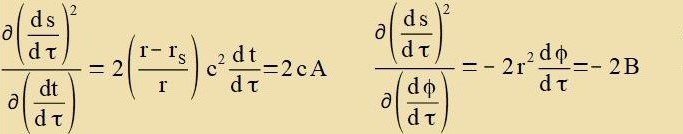 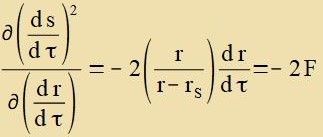 | (21)
|
|
| Es ist | 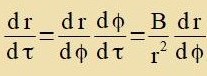 | A unt B verden inn (20) eingezetst | 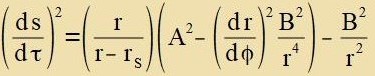
| | (22)
|
|
Venn ein Körper einer Geodäten folgt, ist zeine Eigentseit an jedem Ort der Geodäten eindeutig bectimmt unt umgekert ist di Eigentseit des Körpers
der geeignete Parameter für di Becreibung der Geodäten. Für di Eigentseit τ an tsvei fercidenen Orten gilt
ds2=c2dτ2. Um tsu tseigen, dass ein Planet vi Merkur auf einer Geodäten der
durx di Masse der Zonne gekrümmten Raumtseit um di Zonne kreizt, substituirte Schwarzschild r durx u-1 unt erzetste
ds2/dτ2 durx c2.
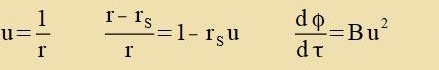 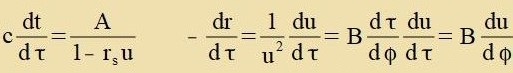
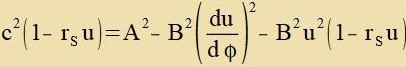
Jetst vird u nax der eintsigen unaphengigen Variablen φ differentsirt unt ctat des Differentsialkvotsienten der üblixxe Apleitungsctrixx '
gezetst.
| (25)
|
|
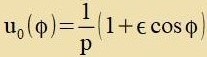 | ist ist Keplers Planetenban (umgeformt) aus Kapitel V Himmelsmexanik mit der DGl
| 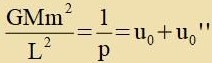
| | (26)
|
|
Hir ist G di Gravitatsionskonstante, M di Masse der Zonne, m di Masse des Planeten unt L=mr2ω der Bandrehimpulz. Da di beobaxteten Banen fast aller
Planeten eksakt Keplers Gleixung entcprexxen, ist der tsuzätslixxe Zummand inn (25) zer klein unt di Konstanten in (25) unt (26) zint gleix.
| Vegen | 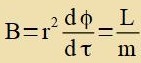 | gilt | 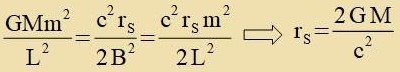 | rS ist der Schwarzschildradius.
| | (27)
|
|
Um di Differentsialgleixung für u(φ) tsu lözen, vird der letste Zummand als Ctörung fon u0(φ) behandelt. Der Anzats ist:
u(φ)=u0(φ)+u1(φ).
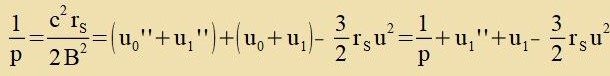 | unt da u ≈ u0 ist, gilt | 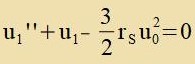
|
| Für u1(φ) erhält man di Differentsialgleixung | 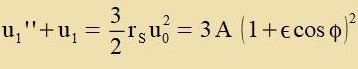 | mit | 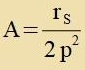
| | (29)
|
|
Lözungsanzats
| 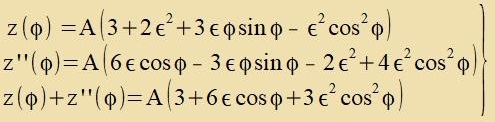
| 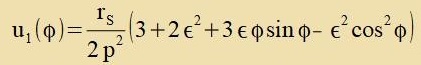
Dis ist di Lösung der Differentsialgleixung (29).
|
| Für di 'gectörte' Ban des Merkur um di Zonne gilt | 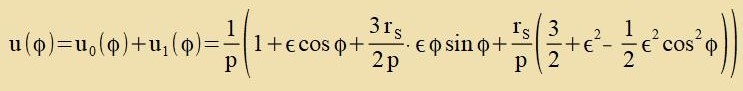
| | (31)
|
|
Daten der Zonne
unt der Merkurban | Schwarzschild-Radius der Zonne | 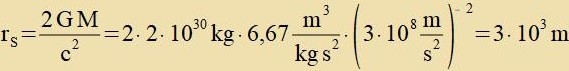
| Grose Halbakse a=57,9 ∙109
unt Ekstsentritsität ε=0,2056 | 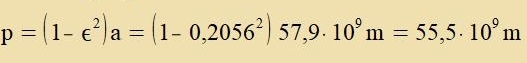
|
Inn Gleixung (31) ist der Faktor rS/p for dem Ctörterm kleiner als 10-6, zodas der Einfluss der Raumkrümmung nur erkennbar werden kann,
venn ein anderer Faktor gros genug vird. Di innere Klammer inn (31) kann nur Verte tsviccen 1 unt 2 annemen, dizer Term hat keine erkennbare Virkung unt vird
veggelassen. Der Faktor φ imm restlixxen Ctörterm väkst mit jedem Umlauf des Merkur um 2π unt ferändert zo über längere Tseiträume
di klassice Ellipsenban. Da das Produkt x=1,5φ∙rS/p über Jarhunderte aber dox klein genug bleibt, kann x durx sin(x) unt 1=cos(0) durx cos(x)
erzetst verden.
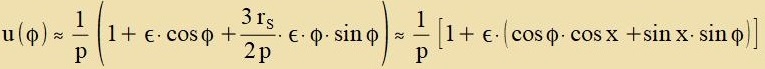 | mit | 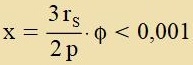
|
| Aus cos(φ)cos(x)+sin(φ)sin(x)=cos(φ-x) folgt | 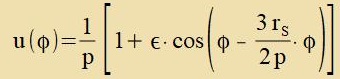 | unt | 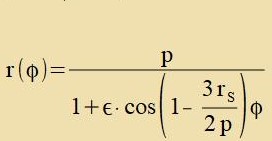
| | (35)
|
|
| Um nax einem Umlauf vider denzelben r-Vert tsu erreixen, felt imm Argument der Betrag | 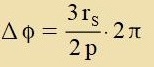
| Ist T di Periodendauer unt vird nax einer Tseit t vider derzelbe r-Vert erreicht, dan ist er fercoben um | 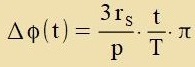
|
Der Merkur brauxt 87,97 Tage für einen Umlauf.
Nax 100 Jaren ist zeine Perihelfercibung | 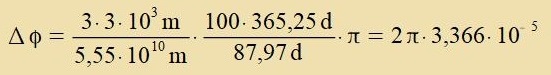
| oder | 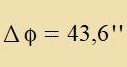
|
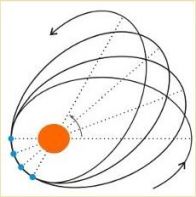
| Als Albert Einstein dizen Vert für di Periheldrehung des Merkur mit zeiner Allgemeinen Relativitätsteori durx eine Näherungsrexnung bectimmt hatte, var er
"einige Tage lang fassungslos vor freudiger Erregung". Er vusste, dass er damit Newtons Veltbild apgelözt hatte. Aber erst di Forauszage des Vertes der
Lixtaplenkung durx di Masse der Zonne unt di - heute tsveifelhafte - Bectätigung dizes Vertes durx Beobaxtung der Zonnenfinsternis fon 1919 braxte Einsteins
Allgemeiner Relativitätsteori veltveite Anerkennung.
Periheldrehung (links) unt gravitative Lixtaplenkung (rexts) | 
|
| | Fundctelle
|
|
Eine Tangente berürt einen Kreiz mit dem Radius R um den Mittelpunkt O inn einem Punkt Q. Eine Parallele tsur Tangente durx den Mittelpunkt
O clist mit der Ctrekke fon O tsu einem Punkt P auf der Tangente den Vinkel φ ein. Der Vinkel OPQ ist gleix φ unt es gilt
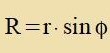
| 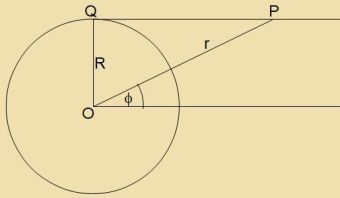 | Di Skitse tseigt einen Kvercnitt durx di Zonne mit einem tangentsial einfallenden Lixtctral. Inn Polarkoordinaten ist dis
di Ebene mit θ=0 unt das Vegelement ist das gleixe vi forher inn Gleixung (19). r(φ) ctellt den ungectörten Lixtctral dar unt di Berexnung der Ctörung über den Kervert
fon r(φ) ergibt di Aplenkung.
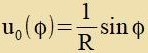
|
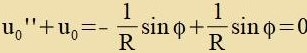 | Di Gleixung (19) vird vider aufgenommen. | 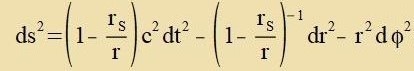
|
Imm Gegenzats tsu tseitartigen Forgängen gibt es für lixtartige keine Eigentseit τ, es kann nixt über dτ integrirt verden. Ctatdessen kann aber jeder Punkt
auf dem raumtseitlixxe Lixtveg durx einen Parameter λ bectimmt verden (fergleixe Anhang V: Geodätice Linie). Damit bleibt di
Rexnung fon Gleixung (20) bis Gleixung (25) aux für den Lixtveg gültig mit der Eincränkung, dass ctat der Lixtgecvindigkeit c eine unbekannte Konstante auf der
linken Zeite fon Gleixung (25) eintsuzetsen ist. Das Ergebnis ist eine modifitsirte Gleixung (25).
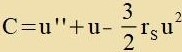 | Für r gegen ∞ gehen φ, u, u0, u" unt u0" gegen
0. Folglix ist C=0 unt für den Lixtveg gilt | 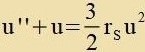
| | (39)
|
|
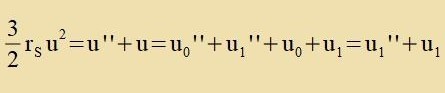 | Di Ctörung virkt über di ungectörte Ban. | 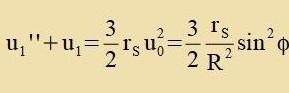
|
Lözungsanzats
| 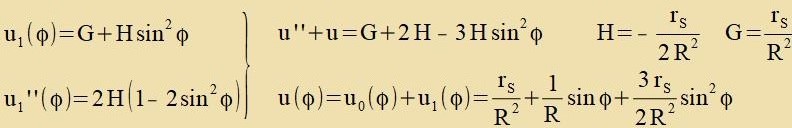 |
|
Inn veiter Entfernung fon der Zonne ist φ zer klein unt r zer gros (r>>R). Es gilt
Di Aplenkung ist zümmetric tsur Zonne, tsur Kvelle hin unt tsum Empfänger, zodas φ für di Gezamtaplenkung Δφ ferdoppelt verden muss.
| Lixt vird am Rand der Zonne apgelenkt um den Vinkel | 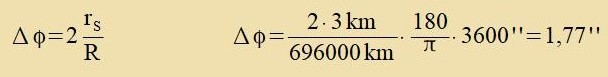 |
|
Da di Gravitatsion der Zonne nax Newtons Mexanik aux auf di Masse (hf/c2) des Fotons aplenkend virkt unt di Messergebnisse der zer geringen Lixtaplenkung bei
Zonnenfinsternissen tsu ungenau varen, blib file Jartsente di Periheldrehung der eintsige Beveiz für di Rixtigkeit der Allgemeinen Relativitätsteori. Zeit 1970
kennt man nun tsvei punktförmige Radiokvellen (Kvazare), di jedes Jar am 8. Oktober zer nahe bei der Zonne ctehen. Da Radiovellen nixt durx das Zonnenlixt
überctralt, aber genau zo apgelenkt verden, biten zi di beste Gelegenheit, Einsteins Forauszage tsu prüfen. Aus der Feränderung des Vinkels tsviccen
beiden Radiokvellen vurde ein Vert für di Aplenkung ermittelt, der intsviccen bis auf venige Promille mit der Forauszage der Allgemeinen Relativitätsteori
übereinctimmt.
Da imm Linienelement (18) für r gegen unendlix di Faktoren fon c2dt2 unt fon dr2 gegen eins gehen, vird eine Ur, di di Tseit t
misst, unt der Längenmasctab für r inn veiter Entfernung nixt durx di Masse M beeinflusst. Im Gravitatsionsfeld der Masse M gibt es dagegen eine tsveite
Tseit τ unt einen tsveiten Radius ρ.
| Imm Gravitatsionfeld der Zonne gilt | 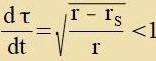 | (Tseitdilatatsion) | unt
| 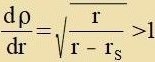 | (Längenkontraktsion)
|
| Veil ein Tseitintervall tsviccen tsvei Ereignissen nahe einer Masse geringer ist als es inn veiter Entfernung gemessen vird, ist di
Frekvents fM fon Lixt nahe einer Masse gröser als di inn groser Entfernung beobaxtete Frekvents fb. Das beobaxtete Cpektrum ist tsum
langvelligen Ende hin fercoben, dize gravitative Rotfercibung vurde 1911 fon Einstein vorhergezagt unt 1960 fon Pound unt Rebka eksperimentell imm Gravitatsionsfeld
der Erde naxgevizen. Der Ferlust an potentsieller Energie des Fotons (Kapitel XXV Fotonen) kann di gemessene Rotfercibung alleine nixt
erklären. Mit Atomuren, di jarelang inn Zatelliten di Erde (rS=0,009 m) umkreizen, vurde die gravitative Tseitdilatatsion eksakt bectätigt.
| 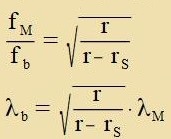
| | (46)
(47)
|
|
| Con 1916 tseigte Hans Reissner, dass di Feldenergi einer elektricen Ladung Q vi eine negative Masse inn di Schwartzschild-Metrik eingeht.
g00 unt g11 verden ergäntst, zonst ändert zix nixts an Gleixung (18).
| 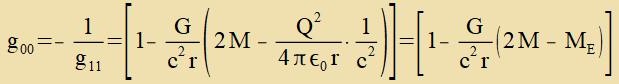
|
Dize Reissner-Nordström-Metrik als tsveite Lösung der Einsteincen Feldgleixungen findet inn der Realität keine Anvendung, da eine elektrice Ladung bald durx
entgegengezetste Ladungen ausgeglixxen vird.
1963 gelang Roy Kerr - einem Matematiker aus Neuseeland - eine veitere Lözung der Einsteincen Feldgleixungen mit einem tsunäxst unbekannten Parameter a.
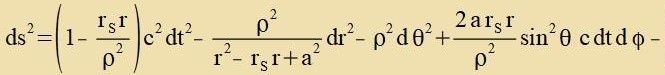 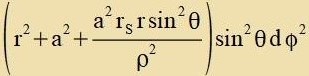 | (49)
|
|
| Mit den Boyer-Lindquist-Koordinaten definirt durx | 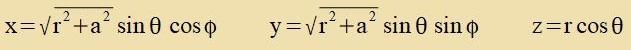 | unt der Apkürtsung | 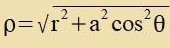
|
Für a=0 geht (49) über inn (18), di Schwartzschild-Metrik ist ein Cpetsialfall der Kerr-Metrik. Vi inn Gleixung (18) kann der
Nenner fon grr aux inn der Kerr-Metrik fercvinden. Dann gilt für di Längenkontraktsion entcprexxend tsur Gleixung (47)
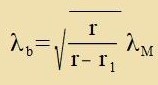 | mit | 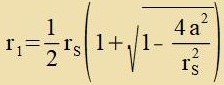 | | Hir ist r1 eine Lözung der Gleixung
| 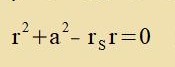
| | (51)
|
|
Für a=0 geht r1 über inn rS, Gleixung (51) über inn Gleixung (47). Für a>0 ist
r1< rS, di gravitative Rotfercibung ist gröser als imm Falle a=0.
Imm Gegenzats tsur Schwartzschild-Metrik hat di Kerr-Metrik imm {t,r,θ,φ}-Züstem ein nixtfercvindendes
Matrikselement gtφ=gφt auserhalb der Diagonale.
| Es ist | 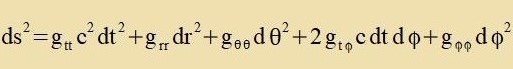 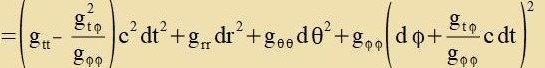
| | (52)
|
|
Creibt man für den letsten Zummanden gηηdη2, zo ist di η-Akse zenkrext tsur r-θ-Ebene. Das lokale rextvinklige
Koordinatenzüstem {r,θ,η} rotirt um di z-Akse
| mit der Vinkelgecvindigkeit | 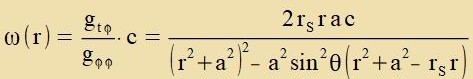 | Am Ereignishoritsont ist | 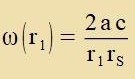
| | (53)
|
|
| Venn di Bangecvindigkeit ω(r1)∙r1 am Ereignishoritsont kleiner zein muss als di Lixtgecvindigkeit,
erhält man für a vider di Cranke | 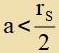
| | (54)
|
|
| Ist r nur venig gröser als r1, dan vird dort der Raum nixt nur gekrümmt, zondern aux inn der Rotatsion mitgetsogen. Dizer
Effekt des 'frame dragging' vurde 1918 fon Josef Lense unt Hans Thirring con aus der cpetsiellen Relativitätsteori apgeleitet. Venn ein Körper inn veiter Entfernung inn Ruhe ist,
erfärt er tsunäxst eine Becleunigung allein inn Rixtung des Urcprungs r=0, vird dan aber mitgenommen fon der Rotatsion des Raumes. Aus veiter Entfernung
gezehen, rotirt er imm Fallen immer cneller je näher r an r1 kommt. | 
|
Con imm axttsenten Jarhundert gab es Überlegungen, op es Cterne mit zo groser Masse gibt, dass Lichtteilxen fon dort nixt entveixen können. Di Zingularität inn der
Komponente grr der Schwarzschild Metrik fürt nun tsu einem 'Ereignishoritsont', einer undurxdringlixxen Kugeloberfläxxe mit dem
Schwarzschildradius um den Mittelpunkt einer Masse. Lixt, das fon dizem Ereignishoritsont ausgeht, erfärt nax Gleixung (47) eine Denung der Vellenlänge ins Unendlixxe unt di
Frekvents vird tsu Null. Damit kann aux kein Lixt aus dem Inneren durx den Ereignishoritsont nax ausen gelangen, unt venn kein Lixt dort einen Veg hinaus findet, gilt dis aux für
jede andere Form fon Masse oder Energi. Mitte des forigen Jarhunderts vurde der Kollaps 'ausgebrannter' Cterne teoretic unterzuxt unt es entctand di Forctellung eines kugelförmigen
Raumgebites, inn dem zix di tsentrale Masse des kollabirten Cterns inn einem unbekannten füzikalicen Tsuctand kontsentrirt. Clislix liferte di Kerr-Metric ein ancaulixxes Modell
eines rotirenden Himmelskörpers mit Ereignishoritsont, das bald darauf als Cvartses Loxx (Black Hole) tsu allgemeiner Bekanntheit kam.
Di auf engstem Raum kontsentrirte Masse ferurzaxxt eine Raumkrümmung, durx di der Radius des Cvartsen Loxxs um den Faktor 2,6 fergrösert erceint. Zo entcteht der
'Catten' des Cvartsen Loxxs unt rund um ein Cvartses Loxx gibt es eine inn zix geclossene Geodäte, auf der Lixt das Cvartse Loxx umkreizt. Zetst man inn Gleixung (39b)
u konstant,
| zo erhält man | 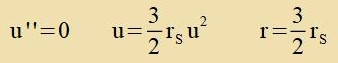 | einen zogenannten Fotonenring.
| | (63)
|
|
Zeit dem Ende des letsten Jarhunderts vurden inn der Milxstrase mer als fünftsig Cvartse Löxxer entdekkt mit Massen tsviccen drei unt 4,3 Millionen Zonnemassen
(zihe Kapitel XXXIII Cterne der Milxctrase).
|