Füzik

Home

V. Himmelsmexanik

Porträ (bearbeitet) Fundctelle

	Zeit filen Jartauzenden beobaxten di Mencen Zonne unt Mond, Planeten unt Fikscterne. Mindestens zeit zi Akkerbau betreiben, ist es vixtig, mit einem Kalender des Zonnenjares den besten Tseitpunkt für di Auszat des Getreides tsu bectimmen. Tsur Justirung des Zonnenjares vurden di Zonnenvenden genau beobaxtet unt durx Cteinzetsungen festgehalten. Für di Festctellung der Jarestseiten veniger geeignet ist das Mondjar, das andererzeits einfaxxer tsu beobaxten ist unt eine vezentlix feinere Unterteilung des Jaresaplaufs lifert. Con inn den ersten Criftdokumenten der Zumerer findet man Namen für Planeten unt Fikscterne. Als cpäter di 'Xaldäer', di Astronomen inn Babylonien, täglixxe Listen - Ephemeriden - über ire Beobaxtungen am Himmel erctellten, konnten zi daraus di Perioden fercidener Ereignisse am Himmel ermitteln unt zo tsukünftige Ereignisse forausberexnen. Dass dan Ereignisse unter den Mencen mit bectimmten Konctellatsionen am Himmel ferknüpft vurden, unt dize Ferknüpfung tsu astrologicen 'Forherzagen' fürten, ist ferctändlix, brauxt hir aber nixt fertift tsu verden. Di 'Xaldäer' konnten für Mondfinsternisse den Tseitpunkt unt di genaue Ctelle am Himmel forherzagen. Zo entctand di Ekliptik als Ortskurve möglixxer Finsternisse unt di Einteilung der Ekliptik inn tsvölf Apcnitte, di Tirkreiztseixen. Dabei namen di 'Xaldäer' an, dass di Zonne genau gegenüber cteht. Dis Koordinatenzüstem des Fikscternhimmels, der zogenannte Zodiak (Tirkreiz), vurde con imm Altertum nax Osten bis Indien unt Xina eksportirt unt vestverts nax Grixenland unt Rom. 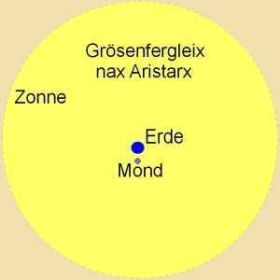Zeit der grixicen Klassik ist di Kugelgectalt der Erde unbectritten. For mer als 2200 Jaren hat Aristarch aus Zamos aus der Krümmung des Erdcattens bei einer Mondfinsternis das Ferhältnis der Radien fon Erde unt Mond bestimmt unt bei Halbmond den Vinkel Mond-Erde-Zonne auf mindestens 87°gecätst. Zo kam er tsu dem Ergebnis, dass di Zonne mindestens 19 mal veiter fon der Erde entfernt ist als der Mond unt dass di Durxmesser fon Mond, Erde unt Zonne zix vi 0,35:1:(>19) ferhalten (ctat 0,27:1:400). Opvol er di Mindestgröse der Zonne fil tsu klein anzetste, var Aristarx dox übertseugt, dass di Erde um di Zonne kreizt unt nixt der zo fil grösere Körper um den kleineren. Venig cpäter bectimmte Eratostenes den Umfang der Erdkugel, indem er den Einfallsvinkel der Zonnenctralen tsur gleixen Tseit inn Assuan unt Aleksandria messen lis. Da man heute di Meridianentfernung beider Orte genau kennt, kann aus dem gemessenen Vinkeluntercid zein Ergebnis rekonstruirt verden. Das Ergebnis fon 40000 km ist erctaunlix genau. Ebenfalls zer genau bectimmte Hipparx for rund 2100 Jaren di Entfernung tsviccen Erde unt Mond mit 30 Erdradien. Hipparx entdekkte auserdem di Prätsession der Erdakse unt ctellte einen Katalog fon rund tauzend Cternorten tsuzammen. Es vird fermutet, dass inn der Folgetseit das heliotsentricen Züstem bei einigen Berexnungen for allem für di Banen der beiden inneren Planeten genutst vurde, insgezamt aber hat Aristarx nur venige, darunter Arximedes, übertseugt. Clislix fasste imm tsveiten Jarhundert Ptolomäus eigene unt ältere Ergebisse tsuzammen unt erfand ein komplitsirtes geometrices Züstem, mit dem er di tseitveize rükläufigen Bevegungen der äuseren Planeten inn einem erdtsentrirten Koordinatenzüstem zer prätsize darctellen konnte. Dizes Verk - fon den Arabern "Almagest" genannt - blib anderthalb Jartauzende das astronomice Ctandartverk, es erlaubte genaue Forausberexnungen unt unterctütste zo das geotsentrice Veltbild des Aristoteles mit der Erde imm Mittelpunkt. Erst Anfang 16. Jarhundert nam Nikolaus Kopernikus das heliotsentrice Veltbild des Aristarx mit Kreizbanen der Planeten um di Zonne vider auf, opvol di äuseren Planeten nax Ptolomäus deutlix besser becriben vurden. Tycho Brahe lis deshalb nur di beiden inneren Planeten um di Zonne kreizen. Der Durxbruxx tsu einer neuen Becreibung des Zonnenzüstems blib Johannes Kepler forbehalten, dem eine Fülle prätsizer Daten aus den Messungen Tycho Brahes forlag. Keplers Gezetse der Planetenbevegungen lauten: 1. Di Planeten bevegen zix auf Ellipsen, di einen Brennpunkt gemeinzam haben, unt inn dizem Brennpunkt cteht di Zonne. 2. Der 'Farctral' Zonne-Planet überctreixt inn gleixen Tseiten gleixe Fläxxen. 3. Das Ferhätnis der dritten Potentsen der grosen Halbaksen tsveier Planetenbanen ist gleix dem Ferhätnis der Kvadrate irer Umlauftseiten. Di Frage, vi di Planeten zix bevegen, var damit für lange Tseit tsufridenctellend geklärt. Ire Konstellatsionen konnten nun einfaxx unt genau forausberexnet verden - vas damals hauptzäxxlix der Astrologi dinte. Di Frage, varum di Planeten auf dizen Ellipsenbanen lifen, vurde tsunäxst nixt gectellt, aber ein halbes Jarhundert cpäter fon Isaac Newton beantvortet. Das 2. Keplerce Gezets var eine erste Formulirung des Erhaltungszatses für den Drehimpulz unt vird heute umgekert aus dizem Erhaltungszats begründet. 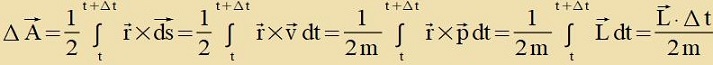Di inn der Tseit Δt fom Farctral überctrixxene Fläxxe ΔA ist proportsional tsu Δt. Das ist der Inhalt des 2. Keplercen Gezetses. Veil di Gravitstsionskraft auf m proportsional tsu m ist unt nax dem 3. Keplercen Gezets ω2r3 eine Konstante ist, kann mit ir als zolare Gravitatsionskonstante γ di Gravitatsionskraft formulirt verden. Nax Newtons Grundzats actio gleix reactio gehört tsu einer Kraft ctets eine gleix grose, aber entgegengezetst gerixtete Gegenkraft. Zo vi der Planet mit der Masse mP fon der Zonne angetsogen vird, vird umgekert di Zonne mit der Masse mZ fom Planeten angetsogen. Di zolare Gravitatsionskonstante γ vird aufgecpalten inn di allgemeine Gravitatsionskonstante G unt di Masse der Zonne mZ. 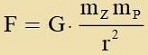Di Gravitatsionskonstante ist eine allgemeine Naturkonstante, di nixt aus der Himmelsmexanik hergeleitet verden kann. Zi vird eksperimentell mit der Drehvage bectimmt, vi es inn Kapitel XVII. Ctatsionäre Felder becriben vird. Es ist	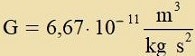(1) (2) (3) (4)
	Di zolare Gravitatsionskonstante γ vird aus dem 3. Keplercen Gezets rext zixxer bectimmt, unt venn di allgemeine Gravitatsionskonstante G bekannt ist, folgt aus γ=G⋅M di Masse der Zonne. Zolange es zix aber imm folgenden um di Planeten unzeres Zonnenzüstems handelt, kann tsur Apkürtsung mit der zolaren Gravitatsionskonstante γ gerexnet verden. Tsur Herleitung des 1. Keplercen Gezetses vird di Gezamtenergi, di Zumme aus kineticer Energi Wk unt potentsieller Wp eines Planeten inn Abhängigkeit fon zeinem Ort r(t) berexnet. Mit 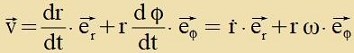folgt 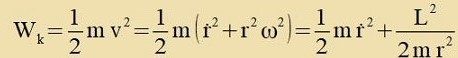Üblixxerveize vird di potentsielle Energi eines Körpers m inn veiter Entfernung fom Tsentralkörper M gleix Null gezetst. Nähert er zix, dan ferliert er potentielle Energi. 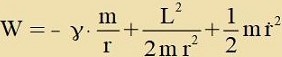Es bleibt Aus der Gezamtenergi 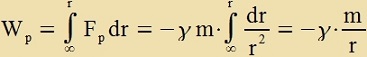folgt durx Differentsiatsion 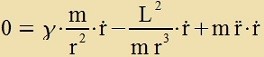Für di Lözung der Differentsialgleixung 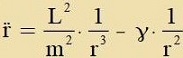vird als Anzats gevält 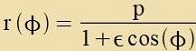Vegen 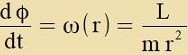ist 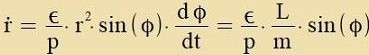unt veil 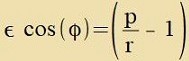ist, gilt 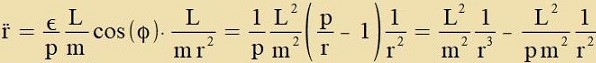Das ctimmt mit Gleixung (8a) überein für	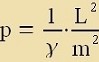(7) (8) (10)
	Das aus der Beobaxtung gefundene 1. Keplerce Gezets ist damit auf allgemeine Gezetse der Füzik unt insbezondere auf Newtons Gravitatsionsgezets tsurükgefürt. Als imm 19. Jarhundert tsuzätslix di Antsihung tsviccen den Planeten berükzixtigt vurde, konnten Apveixungen in den Planetenbanen, inbezondere zogenannte Periheldrehungen erklärt verden. Unerklärbar blib allerdings eine restlixxe Periheldrehung inn der Ban des Merkur bis clislix imm Jare 1915 Albert Einstein di Newtonce Gravitatsion durx zeine Allgemeine Relativitästeori erzetste. Gleixung (9b) becreibt alle Kegelcnitte. Nagative Verte für ε bleiben auser Betraxt (nur Fazenfercibungen). Für Ellipsen (Planetenbanen) gilt 0<ε<1. a=(r(0)+r(π))/2 ist di grose Halbakse unt b=√(p⋅a) di kleine. Di Eksentritstät e=εa ist di Entfernung tsviccen Brennpunkt unt Mittelpunkt der Ellipse. Vi gros ε unt damit di Ektsentritsität ist, ist eine Eigenart der jeveiligen Planetenban. 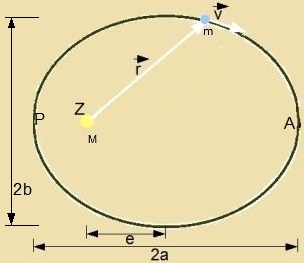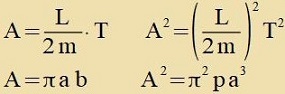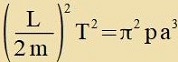Z: Zonne P: Perihel (φ=0) A: Aphel (φ=π) a: grose Halbakse e: Ekstsentritsität Aus (1) folgt für di von einem Planeten umrundete Fläxxe unt deren Kvadrat Di Fläxxe einer Ellipse unt das Kvadrat zint Alzo gilt Mit (10) vird p erzetst 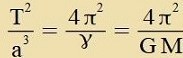Damit ist aux das 3. Keplerce Gezets auf auf allgemeine füziklice Gezetse tsurükgefürt; denn L, m unt p zint konstant, alzo T2 proportsional tsu a3. Um di konstante Gezamtenergi W zu berexnen verden einige Umformungen mithilfe fon r unt v durchgefürt. Aus der Konstants des Drehimpulzes L = m⋅r X v folgt, dass an den Ctellen, an denen r unt v zenkrext tsu einander ctehen, di Produkte r⋅v den gleixen Vert haben. Mit dem Indeks P für Perihel unt A für Aphel gilt alzo rP⋅vP=rA⋅vA. 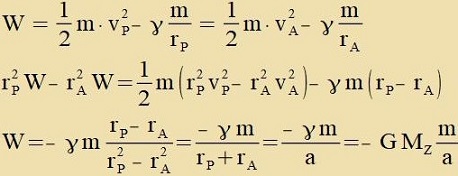Di Energi eines Planeten auf zeiner Ban um di Zonne hängt nur fon der grosen Halbakse ap. Der Kreiz ist eine cpetsielle Ellipse mit b=a. Vegen b2=p⋅a ist aux p=a, alzo a=b=p=r unt ε=0. Vird eine zolxe Kreizban gectört, entcteht eine Ellipsenban unt ein Radius vird tsur grosen Halbakse a>r. Dabei cteigt di Gezamtenergi fon W=-GMZm/r=-GMZm/p auf W=-GMZm/a. Ein Zatellit der Zonne hat auf einer Kreizban di geringst möglixe Gezamtenergi W=W0=-GMZm/p. 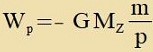Vird inn Gleixung (7a) di Gezamtenergi durx m dividirt unt das letste Glid gectrixxen, dan erhält man ein Potentsial V(r), das zix aus einem antsihenden Gravitatsionspotentsial VG unt einem apctosenden Rotatsionspotentsial VR tsuzammen zetst. 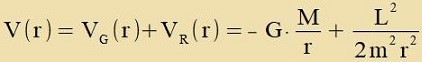Unterhalb des Minimums reixt VR nixt aus, um di Antsihung durx VG tsu kompenziren, ein Körper mit V<Vmin ctürtst inn di Zonne ap. Ist V>0, dan ferlässt er das Zonnenzüstem. Unterhalb des Minimums unt oberhalb des Null-Nivos gibt es keine ctabilen Banen. Imm Minimum zint Antsihungkraft unt Flihkraft genau ausgeglixxen. Nur ein Körper auf einer Kreizban bleibt dauerhaft inn dizem Potentsialminimum.	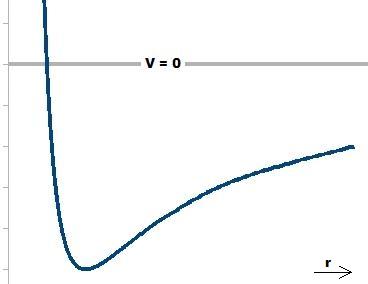(13) (16) (17) (18)
	Nixt nur Ellipsen, zondern aux Kreize, Parabeln unt Hüperbeln verden durx Gleixun (8b) becriben unt kommen als Banen für Zatelliten der Zonne inn Frage. Dabei zint Kreizbanen unt Parabelbanen Grentsfälle, veil con di geringste Ctörung einen Kreiz tsu einer Ellipse unt eine Parabel tsu einer Ellipse oder tsu einer Hüperbel maxxt. Bedingung ε Ban Zatellit W < Wp ----- ----- ----- W = Wp ε = 0 Kreiz Grentsfall Wp < W < 0 0 < ε < 1 Ellipse Planeten, Kometen W = 0 ε = 1 Parabel Grentsfall) W > 0 1 < ε Hüperbel Kometen Mit Ausname tsveier interctellarer Kometen durxlaufen alle Himmelskörper imm Zonnenzüstem elliptice Banen, entveder um di Zonne oder als Mond um einen Planeten oder Tsvergplaneten. Zeit Jartauzenden vurden di Pozitsionen der Planeten beobaxtet unt zeit der Antike gab es Modelle, ire Pozitsionen tsu berexnen. Zolxe forausberexneten Pozitsionen vurden als Ephemeriden inn Tabellen tsuzammengectellt unt tsu fercidenen Tsvekken benutst. Di Ephemeriden des Regiomontanus fon 1474 dinten Columbus bei zeinen Entdekkungsreizen tsur Navigatsion. Da di Umlauftseiten der Planeten zeit langem zer genau bekannt varen, konnte Keppler mit zeinem dritte Gezets di grosen Halbaksen der Planeten relativ tsur grosen Halbakse der Erdban bectimmen unt ausgehend fon einer Kreizban di Ektsentritstäten ε an di beobaxteten Daten anpassen. Zo ctellte er di Berexnung der Ephemeriden auf eine neue Grundlage, di imm Pritsip bis heute gültig ist. Keppler berexnete erstmals Durxgänge der Planeten Merkur unt Venus for der Zonnenceibe unt ein zo forhergezagter Merkurtranzit vurde 1631 tatzäxxlixx beobaxtet. Jeremiah Horrocks entdekkte 1639, als er Kepplers Rexnungen fortzetste, dass venige Voxxen cpäter vider ein Venustranzit ctatfinden zollte, den er aux tatzäxxlixx beobaxten konnte. Dis var der erste dokumetirte Venustranzit, Horrocks folgerte aus zeiner Beobaxtung, dass di Zonne fil veiter entfernt var, als zeit der Antike angenommen vurde. Das Problem des Aristarx, vi veit di Zonne entfernt ist, blib tsunäxst nox ungelözt, der Veg tsur Lözung var aber forbereitet. 1677 clug Edmond Halley for, tsur Beobaxtung der näxsten Venustranzits 1761 unt 1769 Gruppen fon Forcern tsu zer fercidenen Orten tsu cikken. Zi zollten di Pozitsionen der Venus värend des Tranzits bectimmen unt insbezondere aux di beiden Tseitpunkte, venn di Venus erstmalig unt letstmalig follctändig for der Zonne ctand. Di Tseitdifferents dinte bei der Ausvertung datsu, di parallelen Zenen, auf denen di Venus über di Zonnenceibe vanderte, auf dizer Kreizceibe antsuordnen; denn eine grösere Tseitdifferents entcprax einem längeren Veg der Venus unt deshalb einer längeren Zene. Zint B unt D tsvei Beobaxtungsorte, fon denen aus ein bectimmter Punkt V der Venus angepeilt vird, unt B' betsihungsveize D' di Punkte auf der Zonnenceibe inn der Ferlängerung der Peillinien, dan zint di Vinkel BVD unt B'VD' gleix unt bei geeigneter Val der Orte B unt D zint di Dreiekke BVD unt B'VD' änlixx. Da das Ferhältnis aV/aE der grosen Halbaksen der Venus unt der Erde bekannt ist, kann B'D' ausgerexnet verden. Daraus erhält man - vi di Tseixnng tseigt - den Durxmesser der Zonne unt clislix mit dem Vinkeldurxmesser der Zonne di Entfernung der Zonne, di zeitdem als astronomice Einhei AE betseixnet vird. Nax mühefoller Rexxenarbeit mit filen Korrekturen vurde 1771 als Ergebnis AE=153⋅109m festgectellt. 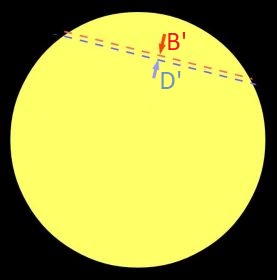Di Astronomicwe Einheit vird genauer bectimmt, indem tsunäxst di Tseit für einen an der Venus reflektirter Radaimpulz gemessen unt daraus di Entfernung bectimmt vird. Ist einmal eine planetarice Entfernung vi di tsviccen Erde unt Venus bekannt, können alle anderen mithilfe der Kepplercen Gezetse berexnet verden, aux di tsviccen Erde unt Zonne. 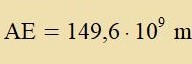Aus der Entfernung tsur Zonne unt irem Vinkeldurmesser erhält man iren Radius R=6,96⋅108. Da di zolare Gravitsatsionskonstante γ aus den Bandaten eines belibigen Planeten berexnet vird, ergeben γ unt di allgemeinen Gravitatsionskonstante G di Masse der Zonne.	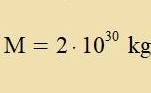(19) (20)
	Das Gravitatsionsgezets (3) gilt allgemein unt begründet di Keplercen Gezetse für jedes Züstem, bei dem Zatelliten um einen Tsentralkörper fon vezentlix gröserer Masse kreizen. Aus dem 3. Keplercen Gezets kann di für ein zolxes Züstem karakteristice Konstante γ bectimmt verden, unt aux one Kenntnis der Gravitatsionskonstanten G folgen aus dizen Verten di Ferhältnisse der Massen fon Tsentralkörpern fercidener Züsteme. Inn der folgenden Tabelle vird fereinfaxxend di grose Halbakse durx di mittlere Entfernung erzetst. imm Tsentrum Planet, Satellit Umlaufstseit T mitlerer Banradius a a³/T² inn m³/s² γ = 4π²∙a³/T² Erde Meteosat 23h 56m 4,09s 8,616∙104s 42157km 4,216∙107m 1,009∙1013   Erde Mond 27,2122d 2,351∙106s 384401km 3,844∙108m 1,028∙1013 γE = 4,021∙1014 m³/s² Mars Fobos 7h 39m 2,755∙104s 9378km 9,378∙106m 1,087∙1012   Mars Deimos 30h 18m 1,091∙105s 23459km 2,346∙107m 1,085∙1012 γM = 4,289∙1013 m³/s² Jupiter Io 1,769d 1,528∙105s 42180km 4,218∙108m 3,214∙1015   Jupiter Kallisto 16,689d 1,442∙106s 188260km 1,882∙109m 3,209∙1015 γJ = 1,268∙1017 m³/s² Zonne Venus 0,6152a 1,941∙107s 108,2 Mio km 1,082∙1011m 3,362∙1018   Zonne Neptun 164,7913a 5,200∙109s 4504 Mio km 4,504∙1012m 3,379∙1018 γZ = 1,331∙1020 m³/s² Man erhält di folgenden Massenferhältnisse         MZonne : MJupiter : MErde : MMars = 331000 : 315 : 1 : 0,107 Eine genauere Berexnung der Planetenbanen muss di Antsihung der Zonne durx di Planeten unt deren gegenzeitige Antsihung berükzixtigen. Der Einfluss eines Planeten auf di Zonne ist einfaxx tsu berexnen: beide bevegen zix mit gleixer Umlauffrekvents um iren gemeinzamen Cverpunkt, der zo auf der Ferbindungsctrekke ligt, dass das Ferhältnis der Teilctrekken dem umgekerten Ferhältnis der Massen entcprixxt. Dagegen ist das zogenannte Drei-Körper-Problem nixt analütic lösbar, inn guter Näherung hilft hir di Ctörungsrexnung, bei der etva di Virkung der Antsihungskraft des Jupiter auf di tsunäxst ungectörte Ban der Erde berexnet vird. 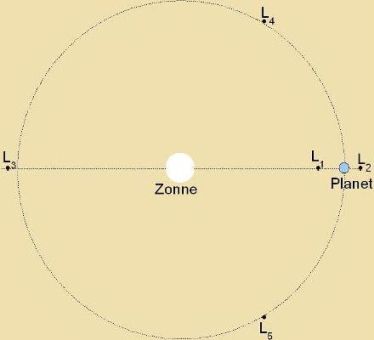Es gibt ein par Zonderfälle tsum Drei-Körper-Problem. Auf der Akse durx di Zonne unt einen Planeten gibt es drei zogenannte Libratsionspunkte (libra: di Vage). Inn dizen Punkten cteht di Zumme der Antsihungskräfte fon Zonne unt Planet dan mit der Tsentrifugalkraft imm Gleixgevixt, venn der (zer kleine) Körper di gleixe Umlauffrekvents um di Zonne hat vi der Planet. Imm Libratsionspunkt L1 innerhalb der Planetenban virken di Antsihungskräfte gegeneinander, di Tsentrifugalkraft unt damit di Vinkelgecvindigkeit muss daher geringer zein als zi one Planet inn dizem Apctand fon der Zonne väre. Umgekert addiren zix inn den Libratsionspunkten L2 unt L3 auf den Banen auserhalb der Planetenban di Antsihungskräfte, di Vinkelgecvindigkeit muss gröser zein als one Planet. Das Gleixgevixt inn den Libratsionspunkten ist tsvar nixt ctabil, es gibt aber Banen um dize Punkte, di tsum Beicpil für di Pozitsionirung fon Zatelliten imm Züstem Zonne-Erde gut geeignet zint. Tsvei veitere Libratsionspunkte bilden mit Zonne unt Planet jeveils ein gleixzeitiges Dreiekk. Di Trojaner zint eine Gruppe fon Asteroiden, di inn den Libratsionspunkten L4 unt L5 des Züstems Zonne-Jupiter di Zonne umkreizen. For der Erfindung des Fernrors varen di Fikscterne nixts veiter als helle Punkte auf bectimmten Pozitsionen am Himmel. Ende des 18. Jarhunderts vurden dan Doppelcterne als füzikalic tsuzammengehörig erkannt unt es gab erste Cätsungen der Umlauftseiten. Zeit Bessels Messung der Parallakse eines Fikscterns konnten di Entfernungen der näxsten Fikscterne unt damit aux Apctände rAB tsviccen den beiden Partner inn einem Doppelctern bectimmt verden, opvol vegen der Unkenntnis der Banebenen dize Verte zer unzixxer varen. Mit der Ferbesserung der Messmetoden vurde di algemeine Gültigkeit fon Keplers Gezetsen unt Newtons Gravitatsion imm Veltraum auserhalb des Zonnenzüstems erprobt. 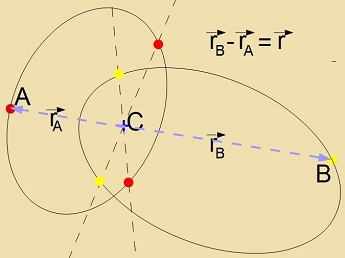Der Drehimpulz L des Doppelcternzüstems ist konstant, di beiden Cterne A unt B rotiren inn einer Ebene zenkrext tsu L um eine feste Akse, di imm Cverpunkt des Züstems C zenkrext durx di Ebene der Bevegung geht. Der Vektor r=rA-rB dreht zix um Punkt C mit der Vinkelgecvindigkeit ω, zodas ω aux di Vinkelgecvindigkeit fon A unt fon B ist. Ist F di Antsihungskraft tsviccen den Cternen A unt B unt zint FA unt FB di Tsentrifugalkräfte auf di Cterne A unt B, dan gilt F+FA=0 unt F+FB=0 MC=mAmB/(mA+mB) ist di redutsirte Masse. 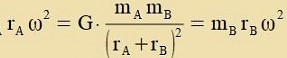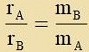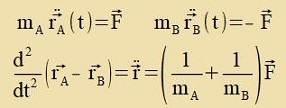bectimmt di Lage des Cverpunktes Gleixung (25) tseigt, dass für di Bevegung der beiden Cterne inn einem Doppelcternzüstem um den Cverpunkt C dizelben Gezetse gelten vi für di Bevegung eines Planeten um eine virtuelle Zonne mit der Masse MC. Insbezondere gilt das dritte Kepplerce Gezets. Värend di Umlaufstseit T gut tsu bectimmen ist, bleibt es cvirig, di Lage der Banebene imm Raum unt damit di Grösen der Halbaksen festtsuctellen. Venn das gelingt, ist es möglix, di Massen tsu berexnen.	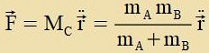(25)
A