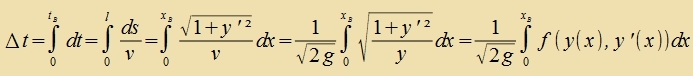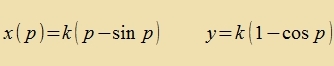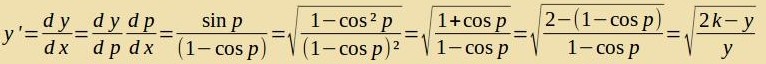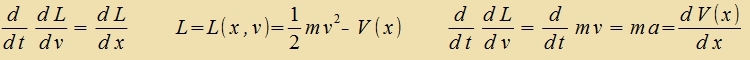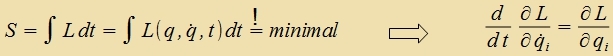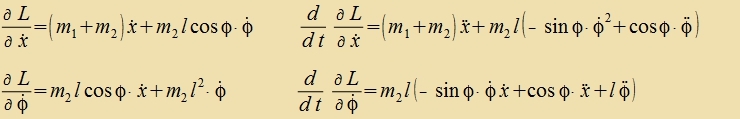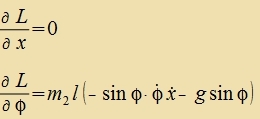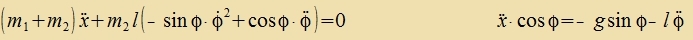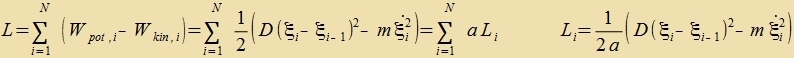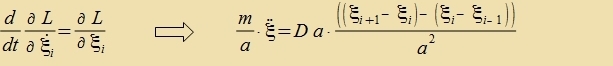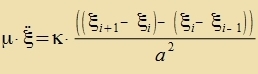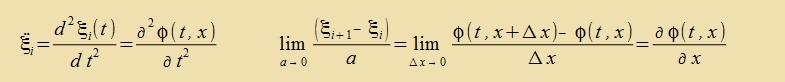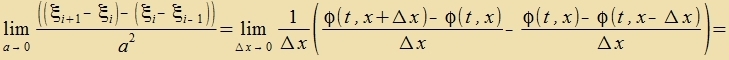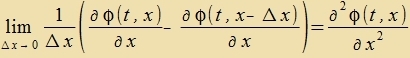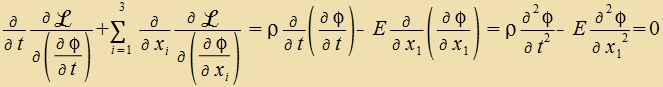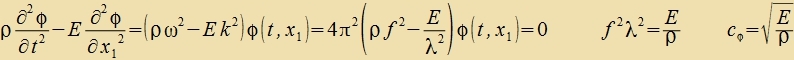Füzik

Home

VI. Analütice Mexanik

Porträ (bearbeitet) Fundctelle

	Di Ban r(t), auf der ein Körper one Reibung inn der kürtsesten Tseit fon einem Punkt A tsu einem tifergelegenem Punkt B gleitet, heist Barüstoxrone. Um eine zolxe Ban tsu berexnen, bedarf es Metoden der analüticen Mexanik, di über di bisher angevandten Metoden hinausfüren. r(t) ligt inn der Ebene, di durx di Punkte A unt B unt durx di Rixtung der Erdantsihung bectimmt ist. Dis zei di x-y-Ebene mit einer nax unten gerixteten y-Akse. Es zei A(0,0),B(xB,yB) unt r(t)=r(x(t),y(t)). Di Ctartgecvindigkeit vA zei gleix 0, dan ist v²(y)=2∙g∙y. Für das Vegelement ds entlang der Ban gilt ds²=dx²+dy²=(1+y'²)dx². Di benötigte Tseit ist	(1)
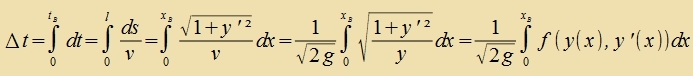
	Värend eine Funktsion aphengig ist fon einer (oder mereren) Variablen, di eine Menge fon Verten aus dem Definitsionsbereix der Funktsion annemen können, ist der Ausdrukk (1) aphengig dafon, über velxe Ban r(t) aus einer Menge fon Banen integrirt vird. Das letste Integral inn (1) ist ein Funktsional, das vercidene Verte annimt je nax dem, über velxe Kurve y(x) unt damit aux y'(x) integrirt vird. Vi di Variatsionsrexnung tseigt, zint di Euler-Lagrange-Gleixungen eine notvendige Bedingung dafür, dass ein Funktsional über eine bectimmte Ban einen minimalen (ekstremalen) Vert annimt imm Vergleix tsu benaxbarten Banen. Venn vi beim Funktsional (1) di Integratsionsvariable nixt eksplitsit imm Integranden forkommt, fereinfaxxen zix di Euler-Lagrange-Gleixungen tsur Beltrami Identität. Mit der Beltrami Identität 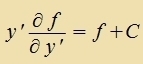unt 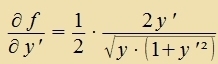erhält man 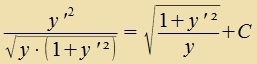Auflözen nax y' ergibt Um tsu tseigen, dass dis di Differentsialgleixung einer Tsükloide ist, geht man aus fon deren Gleixung inn Parameterform.	(3) (5)
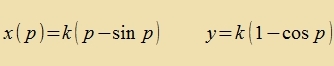
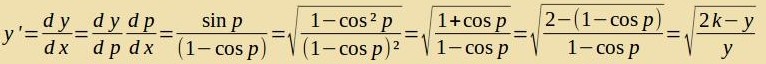
	Für C-2=2k ctimmen di Apleitungen y' inn (3) unt (5) überein, di entsprexxenden Funktsionen y=f(x) unterceiden zix nur durx eine additive Konstante. Di Braxüstone ist eine Tsükloide. 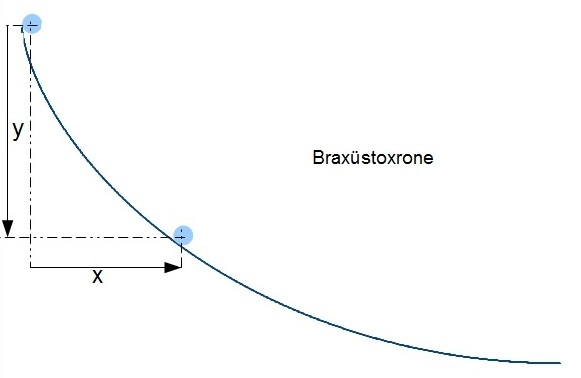Es gibt fercidene Metoden, di Bahn x(t) eines Massenpunktes tsu berexnen. Der jeveilige Ausgangspunkt kann zein 1.   F = m ∙ a (Newton) 2.   Wgez = Wkin+Wpot = const (Hamilton) 3.   S = ∫  L dt = Minimum     mit     L(t,x,v) = Wkin-Wpot (Lagrange) Inn den Kapiteln IV unt V vurden di ersten beiden Metoden für einige Beicpile genutst. Di Metode fon Lagrange bringt neben neuen Möglixkeiten der Berexnung aux eine tifere Einzixt: Ein Körper bevegt zix zo auf zeiner Ban, dass di Virkung S (Einheit Js) geringer ist als bei allen eng benaxbarten Banen (Printsip fon d'Alambert). Di Variatsionsrexnung tseigt, dass das Virkungsintegral S nur dan minimal zein kann gegenüber dem Virkungsintegral benaxbarter Banen, venn di Lagrange-Funktsion L(t,x,v) di folgenden Gleixungen erfüllt 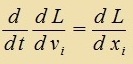Lagrange-Gleixungen (i=1,2,3)	(9)
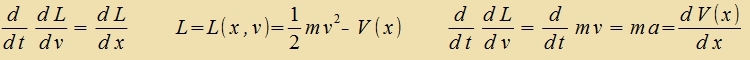
	Um di Übereinctimmung mit der Newtoncen Gleixung tsu tseigen, vird di x-Akse inn der Rixtung der Kraft gelegt, zodas F=(F,0,0), x=(x,0,0) unt v=(v,0,0) ist. Ist V=Wpot das Potentsial einer konzervativen Kraft, zodas ∫ F dx= ΔV folgt, dan ist di Cteigung des Potentsial gleix der Kraft unt di Langrange-Gleixung ctimmt mit der Newton-Gleixung überein. Di Anzätse nax Newton, Hamilton oder Lagrange becreiben das gemeinzame Fundament der Mexanik unt ferliren aux inn keinem anderen Gebit der Füzik ire Gültigkeit. Op man zi als Aksiome anziht oder als durx alle Erfarung begründete Tatzaxxe, ist Gecmakkszaxxe. Di Hamilton- unt di Lagrange-Funktsion zint Skalare, reelle Tsalverte mit der Einheit der Energi. Ire Argumente, di den jeveiligen Ort becreiben, können je nax Problemctellung geeignet gevält verden; zi verden dan ferallgemeinerte Koordinaten genannt unt üblixxerveize mit dem Buxctaben q betseixnet. Um einfaxxe Bedingungen tsu erhalten, müssen di ferallgemeinerten Koordinaten unaphengig fon einander zein. Beispielsveize zint bei einem Pendel, das inn der xy-Ebene cvingt, di beiden kartezicen Koordinaten x unt y nixt unaphengig, vol aber di eine ferallgemeinerte Koordinate φ, der Vinkel gegenüber der Vertikalen. Das Doppelpendel, bei dem am Massepunkt des ersten Pendels ein tsveites Pendel hengt, kann durx tsvei Vinkel becriben verden, di unaphängig foneinander zint. Di Tsal der unahengigen ferallgemeinerten Koordinaten ist der Freiheitsgrad f. Auserdem vird v durx di tseitlixxe Apleitung fon q erzetst. Da aux inn dizer Darctellung das Virkungsintegral minimal zein zoll, folgt vider aus der Variatsionsrexnung di entcprexxende Lagrange-Gleixung.	(11)
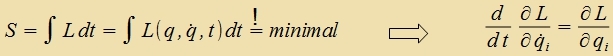
	Di partsiellen Apleitungen, gekenntseixnet durx das Zümbol ∂, bedeuten, dass nur nax den Grösen apgeleitet vird, di eksplitsit inn der Formel für di Langrange-Funktsion ctehen, värend di gemeine Apleitung nax t zix ausvirkt auf jede tseitaphengige Gröse, aux venn di Tseit nixt eksplitsit inn der Formel cteht. Di Bevegungsgleixung eines Planeten um di Zonne - oder allgemeiner eines kleineren Himmelskörpers um ein Tsentralgectirn - di inn Kapitel V (Gl. 7) aus der konstanten Gezamtenergi hergeleitet vurde, erhält man ebenzo mithilfe des Lagrange-Formalismus. Allerdings muss jetst genauer tsviccen kineticer unt potentsieller Energi unterciden verden, vas imm Kapitel V nixt nötig var, veil alle Eintselbeiträge tsur Energi tsuzammen addirt vurden. Bei konstantem Drehimpulz L ist di Rotatsionsenergi auf der Ban aber potentsielle Energi. Man erhält Daraus folgt 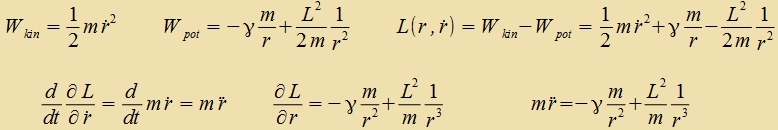Das entcprixxt Gl. (7), Kap. V 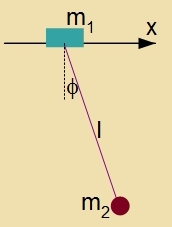An einem Körper der Masse m1, der zix vagerext reibungsloz bevegt, hengt ein Pendel der Länge l mit der Masse m2. Bei der Auslenkung des Pendels um den Vinkel φ ist m2 um h=l∙(1-cos φ) gegenüber der Ruhelage angehoben. 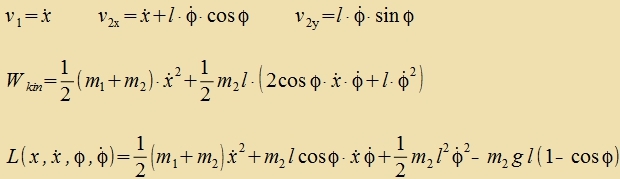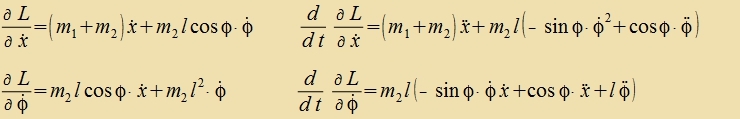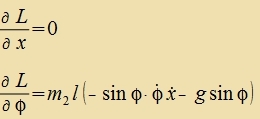Bei dizem Pendel mit beveglixxer Aufhengung erhält man für di Lagrange-Funktsion Zetst man dize Ausdrükke inn di Lagrange-Gleixungen (9) ein, dan erhält man di Bevegungsgleixungen der beiden Massen. 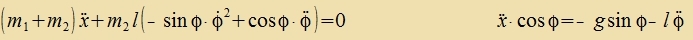Man kann nixt ervarten, dass dize Differentsialgleixungen mit einfaxxen bekannten Funktsionen lözbar zint. Inn der Anvendung vird man fon bectimmten Anfangsbedingungen ausgehend tsunäxst φ(t) numeric berexnen unt damit dan aux x(t) bectimmen können. Fon bezonderem Interesse ist dabei der Einfluss der Parameter m1, m2 unt l. Dis Pendel ist ein Beicpil für einen Cvingungstilger, der in modernen Turmbauten durx Vind oder Erdbeben ausgelözte Eigencvingungen des Gebäudes mildert. m1 cteht für di Masse imm oberen Teil des Gebäudes, dessen Cvingungsenergi an di Pendelmasse m2 teilveize übertragen vird. Historices: Piere Fermat erklärte das Snelliusce Brexxungsgezets mit der Anname, dass Lixt immer den Veg nimt, den es inn kürtsester Tseit tsurüklegt (Fermatces Printsip). Mit Fermats Metoden fand Johan Bernoulli di Braxüstoxrone (βραχυστος: kürtseste; χρονος: Tseit), di Kurve, auf der ein Massepunkt unter dem Einfluss der Cverkraft one Reibung am cnellsten tsu einem tifer gelegenen Punkt gleitet. Johanns Bruder Jakob Bernoulli lözte das Braxüstoxromen-Problem, indem er di neue Infinitezimalrexnung (Leibnitz) anvandte unt legte damit den Grundctein der Variatsionsrexnung. Zein Freund Leonhard Euler baute daraufhin di Variatsionsrexnung aus. Clislix übertrugen d'Alambert unt Lagrange das Fermatce Pritsip auf di Mexanik. Inn einer langen Kette fon Massenpunkten, di durx Federn ferbunden zint, cvingen di Massen m um ire Ruhelage. Di Masse der Federn zei imm Fergleix tsu m fercvindend gering, di Federkonstanten zeien gleix D (zihe Kapitel IV). Di Längenänderung Δl der Federn ergibt zux aus den Auslenkungen ξ aus den Ruhelagen. Ist N di Tsal der Massen, dan ist di Tsal der Federn N-1. Bei zer langen Ketten kann dizer Untercid fernaxläsigt verden. Veiter zei a der Apctand tsviccen den Ruhelagen benaxbarter Massenpunkte, zodas di Länge der Kette gleix l=N∙a ist. Di Lagrange-Funktsion ist dan	(19) (21)
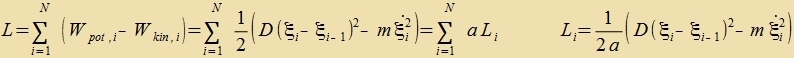
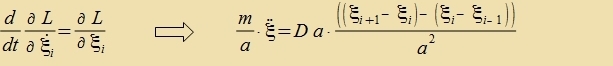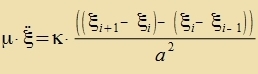
	Jetst zollen Ketten gleixer Länge mit vaksendem N betraxtet verden, zodas a immer kleiner vird. m zoll proportsional tsu a kleiner unt di Federkonstante D umgekert proportsional tsu a gröser verden, zodas zovol di Massenbelegung μ=m/a als aux di Elastitsitätskonstante κ=D∙a gleix bleiben. Für N gegen unendlix geht man fon den diskreten ξi(t) über tsu kontinuirlixxen φ(t,x), vobei di Variable x an di Ctelle des Indeks i tritt. Einen Critt veiter inn der Nummerirung bedeutet dan, dass x um Δx=a gröser vird. Für den Grentsübergang Δx=a gegen Null gilt dan	(22) (23)
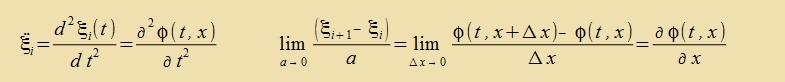
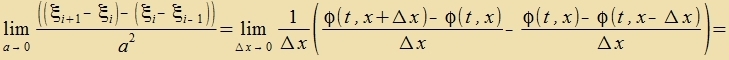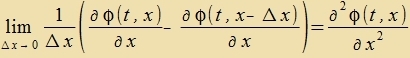
	Di Apleitung nax der Tseit ist nur partsiell, veil der feste Indeks i durx ein festes x erzetst vurde. Aus Gleiung (21) entcteht zo di Gleixung für di longitudinale Bevegung der Teilxen inn einem festen Ctab. Es ist eine Vellengleixung, zi becreibt u. a. di tseitlixxen lokalen Auslenkungen bei Callvellen imm Festkörper.	(24)
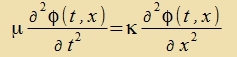
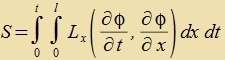
	Venn N gegen unendlix geht, vird di Zumme inn Gleixung (19) tsum Integral unt a=Δx vird tsu dx. Lx ist di Lagrange-Dixte des Feldes φ(t,x), das Integral ist di Lagrange-Funktsion des Feldes unt di Virkung ist Di notvendige Bedingungen dafür, dass dize Virkung - das Funktsional (26) - ekstremal vird, ist	(26)
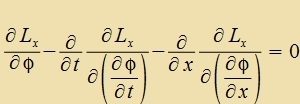	unt venn Lx nixt eksplitsit fon φ aphengt	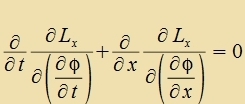(27)
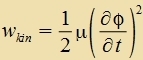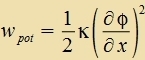
	Beim cvingenden Ctab ist di auf di Länge betsogene Dixte der kineticen Energi unt der potentsiellel Energi Di Lagrangedixte ist 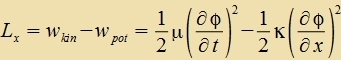Mit Gleixung (27) erhält man	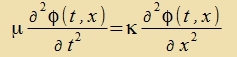(29)
	Di Übereinctimmung der Ergebnisse (24) unt (27) tseigt di allgemeine Anvendbarkeit des Pritsips fon d'Alambert. Di Gleixung (6) inn Kapitel IV gibt di räumlixxe Dixte der Cpannungsenergi inn einem Körper an, der gleixmäsig über zeine gezamte Länge ferformt ist. Venn man mit dizer Gleixung den doppelten Grentsübergang durxfürt, vi er inn den Gleixungen (22) unt (23) becriben ist, vird 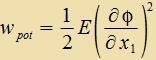unt mit ρ ctat μ für di Massendixte erhält man di Lagrangedixte	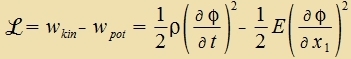(30)
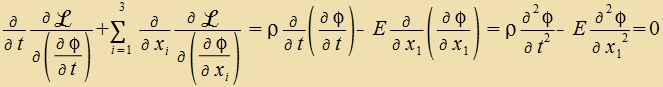
	ℒ ist di lokale räumlixxe Langrangedixte bei lokalen Ferformungen, di überall di gleixe Rixtung haben. Di Anvendung des Lagrange-Formalismus ergibt Mit dem Anzats für eine Velle 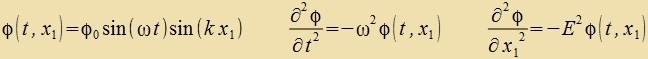erhält man	(33)
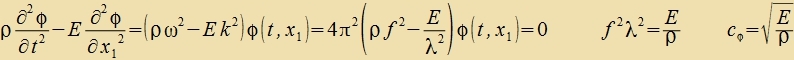
	f ist di Frekvents unt λ di Vellenlänge. Daraus folgt di Gecvindigkeit der longitudinalen Velle cφ=f∙λ imm Medium mit der Dixte ρ unt dem Elastitsitätsmodul E. Gleixung (8) inn Kapitel IV tseigt, dass für Flüsigkeiten unt Gaze eine identice Rexnung gilt, venn nur der Elasatitsitätsmodul E durx den Kompressionsmodul K erzetst vird. Dan erhält man für di Callgecvindig inn Flüssigkeiten unt Gazen	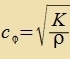(34)
	Di Tabelle tseigt tsum Fergleix di eksperimentellen unt di mit den Gleixungen (33) unt (34) berexneten Verte der Callgecvindigkeit inn fercidenen Ctoffen. Di ctarke Apveixung bei den festen Ctoffen tseigt, dass beim Call lokal nixt allein di longitudinalen Kräfte eine Rolle cpilen. Ctoff ρ [kg/m³] E [MPa/m²] K [MPa/m²] cteo[m/s] ceks [m/s] Apveixung Luft 1,29 - 0,142 332 343 3% Helium 0,179 - 0,164 957 981 2% Vasser 1000 - 2090 1446 1484 3% Kvekzilber 14700 - 38200 1612 1450 -10% Ctal 7850 160000 - 4515 5885 23% Diamant 3510 442000 - 11222 18000 38%
A