Füzik

Home

XXV. Fotonen

Porträ (bearbeitet) Fundctelle

	Jeder Körper apzorbirt unt emittirt ctändig Ctralung (Lixt). Gibt es keinen anderen Energiaustauc tsviccen einem Körper unt zeiner Umgebung unt bleibt zeine Temperatur konstant, zo ist di apzorbirte Ctralungsenergi gleix der emittirten. Ein 'cvartser Körper' zoll keine Frekvents befortsugt apzorbiren oder emittiren; dizem Ideal kommt der zogenannte Holraumctraler am näxsten, ein rusgecvärtster Holraumkörper mit einer kleinen Öffnung. Als Ende des neuntsenten Jarhunderts ausreixend Messergebnisse tsur cpektralen Ctralungsleistung des cvartsen Körpers bei fercidenen Temperaturen forlagen, fand Max Planck durx reines Probiren eine Funktsion mit tsvei angepassten Konstanten α unt β, di tsu allen Ergebnissen passte. T: apzolute Temperatur A: emittirende Fläxxe f: Frekvents der Ctralung β = 4,8∙10-11Ks For allem für den Nenner gab es nixt di geringste teoretice Erklärung. Um Ancluss an di Termodünamik tsu finden, zetste Planck di Boltsmann-Konstante k als Faktor tsur Temperatur T, zodas imm Nenner des Eksponenten di mittlere Energi für ein Züstem mit tsvei Freiheitsgraden cteht (Kapitel IX Gl. (15)). Tsvei Freiheitsgerade ist di Mindesttsal für ein cvingendes Züstem, einen linearen Ostsillator, der di tsvei Freiheitsgrade kinetice Energi unt potentsielle Energi inn einer Rixtung bezitst. Imm Eksponenten entcteht zo aus der Boltzmann-Konstante k unt der angepassten Konstante β eine neue Kostante mit der Dimenzion einer Virkung (J∙s), das Planckce Virkungskvantum h. k=1,381∙10-23J/K (Boltzmann-Konstante) h=6,626∙10-34Js (Planckces Virkungskvantum)	(2)
	Da der Exponent dimenzionsloz ist, ist das Produkt h∙f genau zo vi k∙T ein Energibetrag. Energibeträge - Kvanten -, di deutlix oberhalb der mittleren termicen Energi ligen, kommen, vi der Nenner der Funktsion u(f,T) tseigt, nixt oder nur mit entcprexxend geringer Varceilixkeit for unt verden entcprexxend venig emittirt. Mit dizer Kvantenhüpoteze leitete Max Planck di Kvantenfüzik ein. Aux für di Konstante α fand Planck one genaue Herleitung den rixtigen Ausdrukk. Planckce Ctralungsformel: dP/df ist eine Dixtefunktsion. Um eine Dixte inn Aphengigkeit fon einer anderen Variable dartsuctellen, genügt es nixt, di alte Variable durx di neue tsu erzetsen, inn dizem Fall alzo c/λ anctelle fon f eintsuzetsen. Es muss aux berükzixtigt verden, dass di Dimenzion unt di Intervallbreite zix ändern.	(3) (4)
	Das Maksimum der Ctralung fercibt zix bei cteigender Temperatur tsu höheren Frekventsen unt tsu kürtseren Vellenlängen. Holtskole auf dem Grill beginnt rot tsu glühen unt stralt cpäter gelb oder veis. Gleixtseitig steigt di apgectralte Energi bei steigender Temmperatur. Das zint altbekannte Tazzaxxen, tsu denen es tsvei Gezetse gibt, das Wience Fercibungsgezets unt das Stefan-Boltzmann Gezets. mit gilt mit gilt Di beiden letsten Gleixungen verden numeric gelözt, di Lözungen zint imm Diagramm ferancaulixt. Es ist f(2,822)=3. Bei der Temperatur T ist di Frekvents der maksimalen Ctralungsleistung Es ist f(4,965)=5. Bei der Temperatur T ist di Vellenlänge der maksimalen Ctralungsleistung Das Maksimum imm Cpektrum der Zonne ligt bei λ=4,7⋅10-7m. Dem entcprixxt eine Temperatur T=6100K auf der Zonnenoberfläxxe, der Fotosfäre. Di insgezamt abgectralte Leistung eines cvartsen Körpers inn Aphengigkeit fon der Temperatur ist:	(7) (8) (9)
	Das Integral hat den Tsalenvert π4/15. P=σ⋅A⋅T4 ist das Stefan-Boltzmann Gezets. Di Zolarkonstante E0 gibt di Ctralungsleistung an, di inn der Entfernung einer astronomicen Einheit AE fon der Zonne zenkrext auf eine Fläxxe fällt. Durx di Oberfläxxe einer gedaxten Kugel AK mit dem Radius r = 1 AE um di Zonne geht di Leistung P = AK ⋅ E0 = 4 π (1 AE)2 E0. Um di Temperatur nax dem Stefan-Boltzmann Gezets tsu bectimmen, vird mit dem Radius RZ = 6,96⋅108 m der Zonne ire Oberfläxxe AZ berexnet. E0=1367 W/m² AK=4π⋅(1,496⋅1011m)2=2,81 ⋅1023 m2 P=2,81⋅1023⋅1367 W=3,85⋅1026 W AZ=4π⋅(6,96⋅108 m)2=6,087⋅1018 m2	(10)
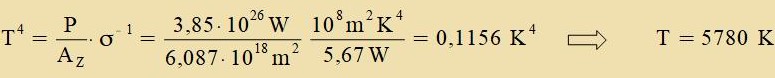
	Di beiden Verte für di Temperatur der Zonnenoberfläxxe unterceiden zix um rund 5%. Der letste Vert vird als effektive Temperatur betseixnet. Värend Planck zeine Kvantenhüpoteze nur auf di linearen Ostsillatoren des ctralenden Körpers anvandte, ging Albert Einstein venige Jare cpäter einen Critt veiter bei der Erklärung des äuseren Fotoeffekts, opvol di damals forligenden Messergebnisse nox venig Hinveize auf zeine Erklärung boten. Er nam an, dass Lixt (Ctralung) immer inn Energibeträgen h∙f emittirt unt apzorbirt vird. Venn Metall mit Lixt bectralt vird, verden Elektronen aus dem Metall herausgeclagen. Di Aplözearbeit W unt di kinetice Energi des Elektrons ctammen fon einem Lixtkvant. Um di kinetice Energi tsu bectimmen, lässt man di Elektronen gegen ein elektrices Feld laufen. Aus der grösten Potentsialdifferents U, di nox fon den Elektronen übervunden verden, erhält man für monokromatices Lixt der Frekvents f di Energigleixung 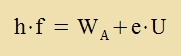Trägt man inn einem Diagramm di Cpannug U gegen di Frekvents f des Lixtes auf, erhält man eine Gerade mit der Cteigung h/e, unt dize Cteigung ist gleix für alle Metalle. Einsteins forveggenommene Erklärung des Fotoeffektes vurde inn der Folgetseit durx jeden Ferzux bectätigt. Di Frekvents des Lixtes bectimmt den Energibetrag des Fotons, das vi ein Teilxen oder Korpuskel auf das Metall trifft unt ein Elektron herausclägt. Di Tsal dizer Fotonen bectimmt di Intenzität des Lixtes. Das gleixe gilt für alle anderen Vellenbereixe der elektromangneticen Ctralung. Da Energi cver unt träge ist, bezitsen di Fotonen di irem Energibetrag entcprexxende Masse unt einen Impulz.	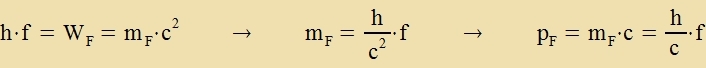(12)
	Eine Masse m, di fon einem Turm der Höhe H fällt, ferlirt di potentsielle Energi m∙g∙H. Daszelbe geciht mit einem Foton, dessen Energiferlust tsu einer Frekventsänderung fürt. 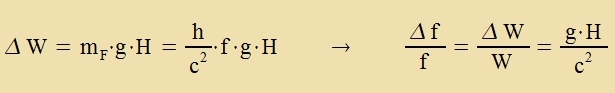Zetst man, um di Grösenordnung dizer Frekventsfercibung tsu klären, eine Höhe fon 100 m ein, zo erhält man für Δf/f einen Vert um 10-14. Tatzäxxlix vurde es mit dem Mößbauereffekt möglix, mit γ-Ctralen di nötige Auflözung tsu erreixen, um dize Frekvenfercibung naxtsuveizen. Beim Compton-Effekt trifft ein γ-Foton auf ein Elektron unt vird aus zeiner urcprünglixxen Rixtung um den Vinkel α apgelenkt. Dabei ferlirt es Energi unt fligt mit geringerer Frekvents veiter. Di kinetice unt di Bindungsenergi des Elektrons for dem Ctos ist fernaxlässigbar gegenüber der Energi des Fotons, naxher dagegen zo hox, dass zi relativistic gerexnet verden muss (Gl. (32) Kapitel XXII). Imm folgenden zoll der Indeks 0 für das einfallende γ-Foton ctehen, E für das Elektron unt kein Indeks für das gectreute Foton. Energierhaltung Impulzerhaltung Der Impulz des Elektrons kann eliminirt verden:     Daraus erhält man mit dem Impulz des Fotons nax Gleixung (5) unt der zogenannten Compton-Vellenlänge λC Di Vellenlänge des inn Rixtung α gectreuten Fotons ist	(20)
	Compton bectralte Grafit mit Röntgenctralen unt fand di Änderung der Vellenlänge (Frekvents) unt eine rükverts gerixtete Ctreuung, di beide nixt mit der Forctellung des Lixtes als Velle fereinbar zint. Di Erklärung des Compton-Effektes ferlangt, das Foton als Teilxen mit Impulz unt Energi tsu behandeln. Fast drei Jarhunderte ferctand man di Forctellungen des Lixts als Teilxen oder Velle als unfereinbare Gegenzätse. Ctat dizes Vidercpruxs gilt heute di Forctellung eines Dualismus Velle-Korpuskel: Lixt breitet zix als Velle aus unt bei der Vekselvirkung mit Materie ferhält es zix vi ein Korpuskel. Ein Ferzux, der beides gleixtseitig demonstrirt, ist der Doppelcpaltferzux mit zer geringer Intenzität, zodass eintselne Fotonen registrirt verden können. Das Ergebnis ist das gleixe, vi beim entcprexxenden Ferzux mit Elektronen, der imm näxsten Kapitel becriben vird.
A