 Füzik |  Home | XXI. Lorentz-Transformatsionen
|  | Porträ (bearbeitet) Fundctelle |
 Füzik |  Home | XXI. Lorentz-Transformatsionen
|  | Porträ (bearbeitet) Fundctelle |
| 1) Di Koordinatentransformatsionen der klassicen Mexanik Nax Kant zint Raum und Tseit Ancauungen, di der Menc a priori hat, alzo nicht durx Erfarung lernt. Demnax gibt es nur einen Raum unt eine Tseit, die für alle Mencen gleix zint, di Grösen fon Längen unt Tseitintervallen zint abzolut, verden alzo fon jedem gleix gros gemessen, fon vo aux immer gemessen vird. Bis tsum Ende des neuntsenten Jarhunderts galt di folgende Umrexnung tsviccen tsvei Koordinatenzüstemen, di heute Galilei-Transformatsionen genannt verden, als zelbstferctändlix.
| (1) | ||||||||||||||||||||
| 2) Der Michelson-Ferzux vidercprixxt den Galilei-Transformatsionen Zeit dem Anfang des neuntsenten Jarhunderts ctand aufgrund der Doppelcpaltferzuxe fon Thomas Young fest, dass Lixt zix als Velle ausbreitet. Da alle bekannten Vellen ein Medium brauxen, hatte con Christiaan Huygens einen Äter als Medium für di Lixtausbreitung postulirt. Nax Fresnel zollte der Äter im apsoluten Raum ruhen aber teilveize fon Materie mitgenommen verden. Mit dizer Forctellung vurde di Aberratsion des Lixtes fon Cternen imm bevegten Fernror und di Mitname des Lixtes durx ctrömendes Vasser imm Ferzux fon Fizeau erklärt.
Tsuzammen mit Edward Morley viderholte Michelson das Eksperiment 1887 mit ferbesserter Genauigkeit. Di Ausvertung aufgrund der Äterteori ergab eine Gecvindigkeit von höxstens 8 km/s stat der tsu ervartenden 30 km/s. Trotsdem blib di Forctellung, Lixt unt alle elektromangneticencen Vellen bräuxten tsur Ausbreitung ein Medium, den Äter, nox fast tsvantsig Jare Konzens unter den Füzikern. Eine punktförmigen Kvelle zendet eine Kugelvelle aus. Inn einem Züstem, das zix gegenüber der Kvelle bevegt, erceint dize Kugelvelle bei Anvendung der Galilei-Transformatsionen fertserrt. Das ist auch tatzäxxlix der Fall bei Vellen, di zix inn einem Medium ausbreiten. Als Woldemar Voigt 1887 di Frekventsvercibungen des Lixtes beim Doppler-Effekt inn den fercidenen Rixtungen tsur Bevegung der Kvelle behandelte unt di Fertserrung für unrealistic hilt, formulirte er neue Transformatsions-Gleixungen, bei denen erstmals aux di Tseit transformirt wurde. Mit dizer Transformatsion bleibt die Kugelvelle erhalten.
| (2) | ||||||||||||||||||||
|
Di Folgen dizer Gleixungen vären gevezen: di Konstants der Lixtgecvindigkeit, eine Längenkontraktsion zenkrext tsur Relativgecvindigkeit v unt eine Tseitdilatatsion
Δt'≠Δt. Venn tsvei Ereignisse inn einem Züstem an vercidenen Orten gleixtseitig gecehen, vären zi aus einem anderen Züstem nax einander tsu
beobaxten. Aber Voigt wollte dize Gleixungen nicht als allgemeines Transformatsionsgezets verctanden vissen. Gegen Ende des neuntsenten Jarhunderts cuf Hendrik Lorentz eine neue Äterteori, inn der er tsviccen der mit dem Äter ferbundenen Tseit unt einer Ortstseit untercid. Zo konnte er di Aberratsion des Lixts unt den Ferzux fon Fizeau erklären. Für di Umrexnung fom Züstem der Ortstseit inn das des Äters entvikkelte er di Lorentz-Transformatsionen (12), di Einstein venig cpäter tsur Grundlage zeiner Relativitätsteori maxxte. Lorentz zelbst hilt di Ortstseit allerdings für eine reine "Arbeitshypothese" one füzikalicen Gehalt. Vi Voigt vollte er di abzolute Tseit nixt aufgeben.
| |||||||||||||||||||||
3) Di Tseit ferläuft nixt immer gleix Venn zix das Lixt immer mit der gleixen Gecvindigkeit ausbreitet unaphengig fon der Gecvindigkeit der Kvelle, des Empfängers oder eines Beobaxters, dan müssen di Gleixungen (1) - di zogenannten Galilei-Transformatsionen - grundzätslix inn Frage gectellt verden. Aux di Tseit darf dafon nixt ausgenommen bleiben. Venn dizelben Ereignisse aus fercidenen Betsugszüstem beobaxtet verden, müssen alle Variablen, di dize Ereignisse becreiben, tsunäxst untercidlix betseixnet verden. Di eintsige unt vezentlixxe Ausname ist di Lixtgecvindigkeit c, di immer den gleixen Vert hat. Inn einem Gedankeneksperiment vird Lixt tsur Kvelle tsurükgecpigelt. Lixtkvelle, Empfäger, Cpigel unt Ur zint inn einem Betsugszüstem inn Ruhe (Ruhzüstem), värend ein Beobaxter zenkrext tsum Lixtveg mit der Gecvindigkeit v forbei fligt. Es vird angenommen, dass Längen zenkrext tsu v unferändert gemessen verden (y'=y).
| (4) | ||||||||||||||||||||
|
Lässt man alzo tsu, dass di Tseit inn tsvei Betsugszüstemen untercidlix ferläuft (t’ ist nixt gleix t), dan folgt aus der Konstants der Lixtgecvindigkeit ein Untercid imm Tseitintervall tsviccen tsvei Ereignissen, venn dize aus fercidenen Betsugszüstemen beobaxtet verden. Veil di Konstante γ, di nur fon der Lixtgecvindigkeit unt der Relativgecvindigkeit der beiden Züsteme aphengt, gröser als eins ist, ist Δt' gröser als Δt: imm Ruhzüstem ist das Tseitintervall am kürtsesten (Tseitdilatatsion). Dize Bezonderheit des Ruhzüstems rürt daher, dass di Tseiten dort am gleixen Ort gemessen verden. Di Transformatsionsformel für di Tseit zollte deshalb aux einen Zummand mit der Ctelle x, an der di Tseit gemessen vird, enthalten. Da tsu Anfang des 20. Jarhunderts zo geringe Tseituntercide kaum messbar cinen unt andererzeits di Forctellung einer apzoluten Tseit allgemein als zelpstferctändlix galt, vurde Einsteins Relativitätsteori meist als blose Teori apgetan. Intsviccen gibt es Gebite des täglixxen Lebens (Navigatsionsgeräte), vo one Berükzixtigung der Relativitätsteori Feler auftreten. Heute verden Tseit- unt Längenmessung auf atomare Forgänge tsurükgefürt, zodass es für filozofice Definitsionen einer apzoluten Tseit oder eines apzoluten Raumes keinen Bedarf mer gibt. | |||||||||||||||||||||
4) Das Ortsglid inn der Tseittransformatsion Di cpetsielle Relativitätsteorie behandelt di Transformatsion der füzikalicen Grösen tsviccen tsvei Inertsialzüstemen, alzo tsviccen tsvei Betsugszüstemen, di nixt becleunigt zint, zondern zix mit konstanter Gecvindigkeit tsu einander bevegen. Di x-Aksen beider Züsteme zint regelmäsig gleixgerixtet unt parallel tsur Relativgecvindigkeit v=(v,0,0). Vi con imm letsten Apcnitt bleiben di Längen zenkrext tsu v unferändert, värend di Tseit auf einfaxxste Veize als ortsaphängig angenommen vird. Di Konstante α zei vi γ nur fon v unt c, aber nixt fon x oder t aphengig. 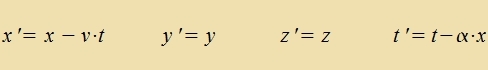 Eine Kvelle Q zendet ein Lixtzignal aus, dessen Ausbreitung entlang der x-Aksen tsveier Inertsialzüsteme beobaxtet vird. Alle Tseiten unt Koordinaten am Ort unt Tseitpunkt der Lixtauszendung zeien gleix Null. Di Kvelle bevegt zix belibig, zi muss nur imm Moment der Lixtauszendung imm dan gemeinzamen Koordinatenurcprung ligen. 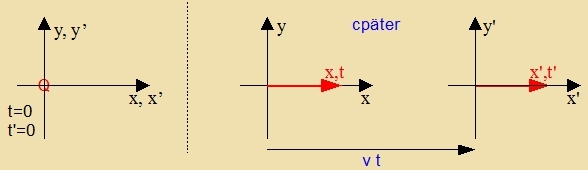  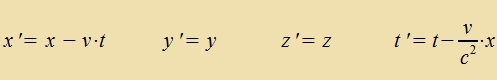 Dize Formel ist nixt rixtig, vi imm näxsten Apcnitt getseigt vird. Zi ist eine Art Tsviccenergebnis. | (6) | ||||||||||||||||||||
5) Das Relativitätsprintsip unt di Lorentz-Transformatsionen Imm Laufe der Gecixte hat man tsuerst di Erde als Mittelpunkt der Velt angezehen, cpäter di Zonne. Ende des 19. Jarhunderts vusste man, dass zix aux di Fikscterne bevegen, alzo aux di Zonne. Trotsdem blib das Bevusstzein fest ferankert, dass es einen ruhenden Raum geben müsse, inn dem zix di Himmelskörper bevegen. Inn dizem ruhenden Raum zollte zix das Lixt ausbreiten vi di Meresvellen über dem festen Meresgrund. Da ein Punkt der Erdoberfläxxe zix imm Laufe fon 24 Ctunden infolge der Erddrehung inn entgegengezetsten Rixtungen bevegt, hoffte man, aus untercidlixxen Lixtgecvindigkeiten etvas über dizen ruhenden Raum tsu erfaren. Das var Michelsons Tsil. Aus dem unervarteten Ergebnis der Michelson-Ferzuxe tsog Einstein den Cluss, dass gar kein ruhender Raum eksistirt. Es gibt nur belibig file Inertsialzüsteme mit bectimmten Relativgecvindigkeiten, fon denen aber grundzätslix keines fon bezonderer Bedeutung ist (Relativitätsprintsip). Durx di Ferzuxsanordnung verden allenfalls di Betsihungen inn einem cpetsiellen Inertsialzüstem bezonders einfax. Di Naturgezetse gelten untercidsloz inn allen Inertsialzüstemen; um allerdings Beobaxtungen aus einem anderen Züstem als dem eigenen tsu ferctehen, muss man di Grösen rixtig umrexnen (transformiren). Nax dem Relativitätsprintsip müsste di Gleixung (6) folgendermasen ergäntst verden. 
| (7) | ||||||||||||||||||||
Di Gleixungen (6) unt (7) füren tsu einem Vidercpruxx.
Di Formeln für di Umrexnungen fon Ort unt Tseit eines Ereignisses, das aus tsvei Inertsialzüstemen beobaxtet vird, zint di Lorentstransformatsionen.
| (12) (13) | ||||||||||||||||||||
Tatzäxxlix ctellt di Transformatsion (12) nur einen Cpetsialfall der Lorentz-Transformatsionen dar, der Lorentz-Boost genannt vird. Imm allgemeinen Fall muss tsunäxst das Koordinatenzüstem zo gedreht verden, das eine Akse - fornemlix di x-Akse - parallel tur Relativgecvindigkeit v ligt. Dan vird ein Lorentz-Boost angevendet unt clislix vider eine Drehung, um di Tseit unt di Koordinaten eines Ereignisses imm Züstem des Beobaxters tsu erhalten. Mer datsu findet man imm Kapitel XXIII. Raum-Tseit unt imm Anhang L (Lie-Gruppen) . | |||||||||||||||||||||
6) Lorentz-Kontraktsion, Tseitdilatatsion unt Gleixtseitigkeit Erste Anvendungen der Lorentz-Transformatsionen tseigen, dass ein bevegter Gegenctand inn der Bevegungsrixtung verkürtst erceint. Dabei müssen Anfangs- unt Endpunkt des Gegenctandes imm Züstem des Beobaxters (x', t') gleixtseitig gemessen verden. 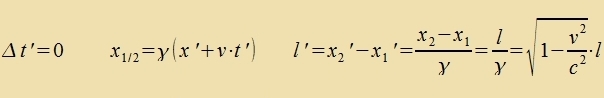 Dize Ferkürtsung aller Längen parallel tsur Relativgecvindigkeit v vird Lorentz-Kontraktsion genannt. Tseitintervalle verden, vi con becriben, gedent. Dabei muss der Ort imm Ruhzüstem (x, t) gleix bleiben. 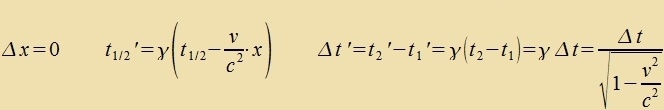 Man cprixxt fon einer Tseitdilatatsion. Finden tsvei Ereignisse inn einem bectimmten Inertsialzüstem gleixtseitig an fercidenen Orten ctat, zo verden zi aus einem anderen Inertsialzüstem nixt als gleixtseitig vargenommen. 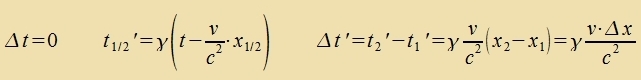 Di tseitlixxe Reihenfolge tsveier Ereignisse an fercidenen Orten kann zix - aus anderen Inertsialzüstemen beobaxtet - zogar umkeren. Venn di tseitlixxe Änderung einer füzikalicen Gröse inn fercidenen Inertsialzüstemen ferglixxen verden zoll, brauxt man di Apleitung der Funktsion t'(t). Venn mit der Eigentseit einer Ur auf einem festen Plats inn einem herforgehobenen Inrtsialzüstem gerexnet vird, creibt man oft t(τ).
| (18) | ||||||||||||||||||||
7) Der Dopplereffekt für Lixt Eine Kvelle zendet Lixt der Frekvents f, alzo mit der Periodendauer Δt=T=1/f. Ein Beobaxter, der zix mit der Gecvindigkeit v fon der Kvelle entfernt, misst di Frekvents f'=1/T'. Di Tseit T' tsviccen tsvei auf einander folgenden Vellenmaksima vird berexnet aus der Dilatatsion des Tseitintervalls Δt =T unt der Fercpätung eines Maksimums, das einen um s=v∙Δt längeren Veg gegenüber dem forausgegangenen tsurükklegen muss.
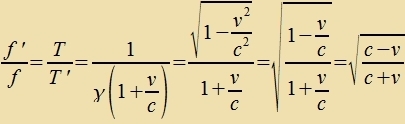 | (20) | ||||||||||||||||||||
|
Vi imm nixtrelativisticen Fall nimmt di Frekvents bei einer Fergröserung der Entfernung ap, für Lixt bedeutet das eine Rotfercibung. Bei einer Annäherung tsviccen
Kvelle unt Beobaxter bleiben Rexnung unt Ergebnis gleix, nur muss v durx -v erzetst verden. | |||||||||||||||||||||
| A | |||||||||||||||||||||