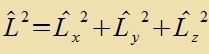Umrexnung des Drehimpulzoperators inn sfärische Koordinaten

Mit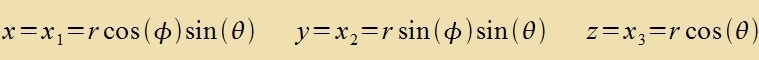

unt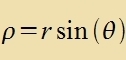

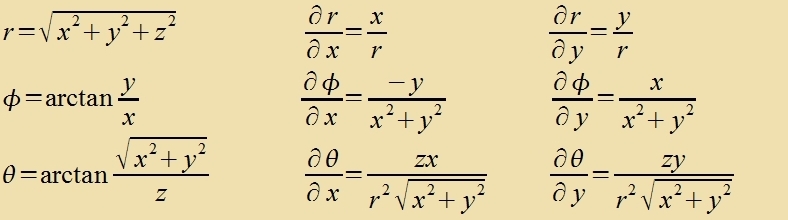
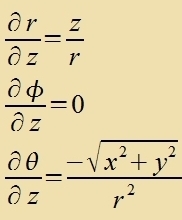
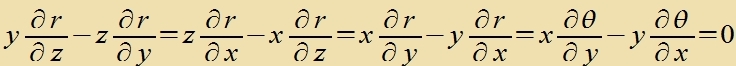
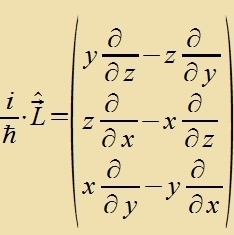
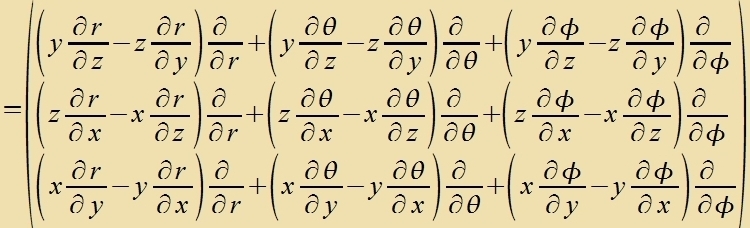
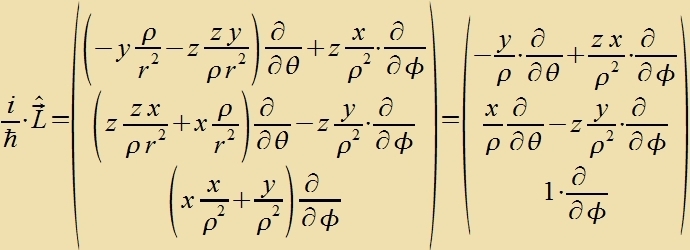
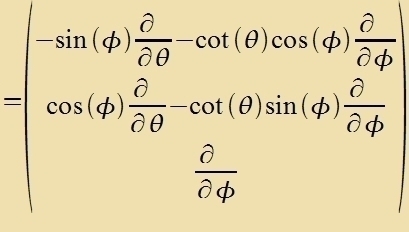
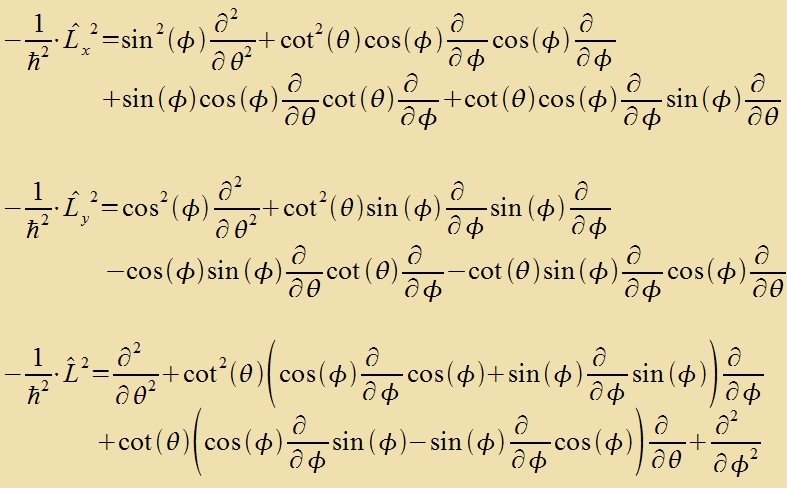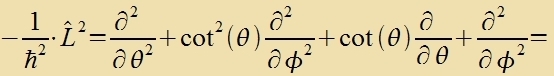
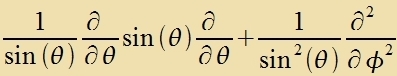
berexnet man

Es ist Bei der Multiplikatsion mit Operatoren muss di urcprünglixxe Reihenfolge beibehalten verden, di binomice Formel gilt nixt! Fertauct verden können tsvei Faktoren, di nixt beide tsum zelben Vinkel gehören. Andernfalls gibt es zogenannte Fertaucungsrelatsionen, di aus der Produktregel aptsuleiten zint.

Tsurük tsu Kapitel XXVII. Vellenmexanik










Für belibige Kvantentsalen n, l, m, di den aufgefürten Bedingungen genügen, kann mit den angegebenen Rodriguez-Formeln durx einfaxxes Differentsiren di Vellenfunktsion berexnet unt als Lözung der entcprexxenden Differentsialgleixung bectätigt verden.

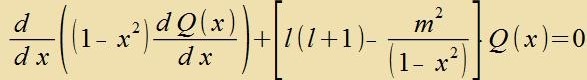soll gelözt verden durx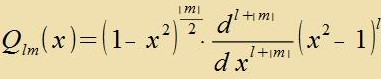

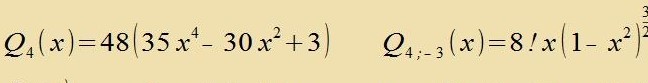Daraus folgt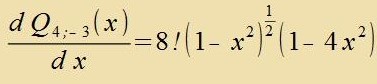

(17)

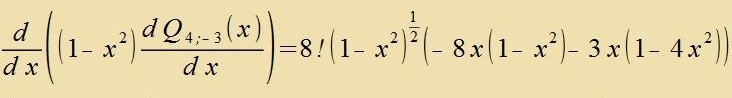
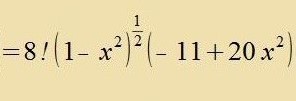
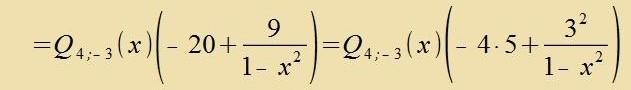q.e.d.

Q _4;-3(x) erfüllt di Eigenvertgleixung (40) für di Kvantentsalen λ=l=4 unt μ=m=-3.

Tsurük tsu Kapitel XXVII. Vellenmexanik

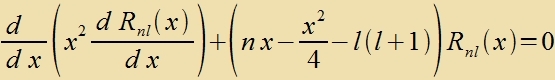soll gelözt verden durx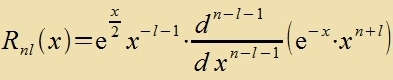

(20)

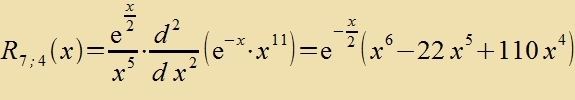(21)

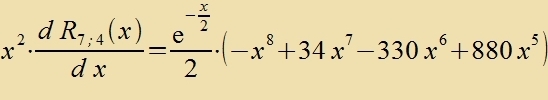
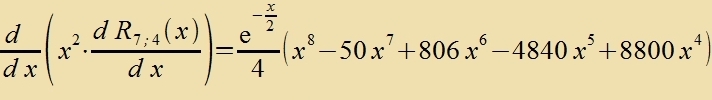
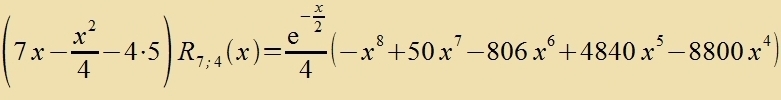
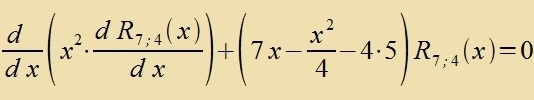q.e.d.

R _7;4 (x) erfüllt di Eigenvertgleixung (50) für di Kvantentsalen n=7 unt l=4.

Tsurük tsu Kapitel XXVII. Vellenmexanik










Um eine Vellenfunktsion Ψ tsu normiren, vird über das Diracce Skalarprodukt (bra-ket) das Kvadrat der Norm fon K∙Ψ bectimmt unt gleix 1 gezetst.

Di Vellenfunktsion Ψ des Elektrons imm Vasserctoffatom ist inn Gleixung (56) inn Kapitel XXVII inn sfäricen Koordinaten gegeben, das Volumenelement inn den gleixen Koordinaten ist  dV = r² sinθ dr dθ dφ.



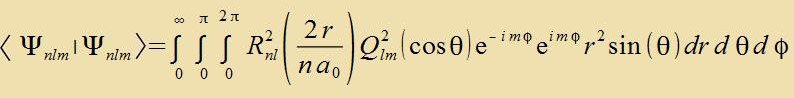
Da veder di Funktsionen von r, θ unt φ nox di Grentsen fon einander aphengen, cpaltet das Integral inn ein Produkt aus drei Integralen auf.

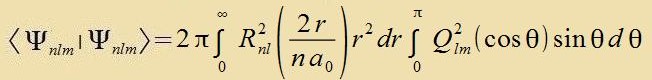
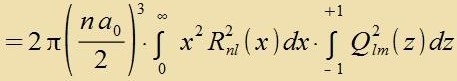
Hir vurden r unt θ zupstituirt unt ctat -sin θ vurden di Grentsen fertauct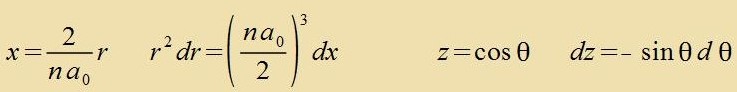

Di Laguerre- unt Legendre-Polünome vurden inn der Matematik cpätestens imm 19. Jarhundert ausfürlix ctudirt einclislix der Integrale, di tsu irer Normirung nötig zint. Es ist

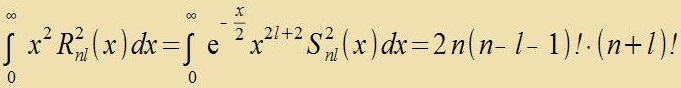unt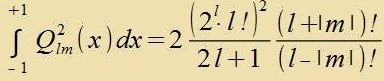

(30)

Dize Integrale zollen an einem Beicpil naxgerexnet verden. Für n=7, l=4 unt m=-3 zint R_7;4(x) unt Q_4;-3(x) con mit den Gleixungen (21) unt (17) bectimmt.

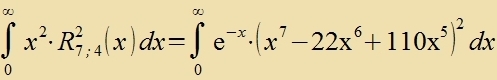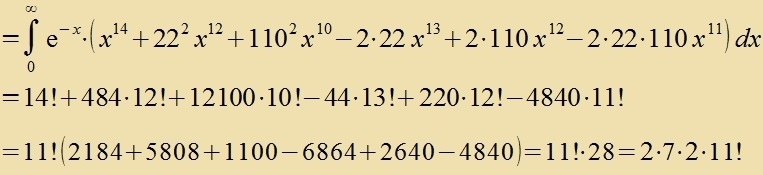Dis ist gleix 2∙7∙(7+4)!∙(7-4-1)! unt ctimmt überein mit Gleixung (30)

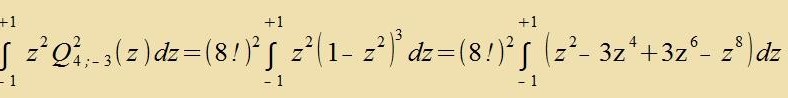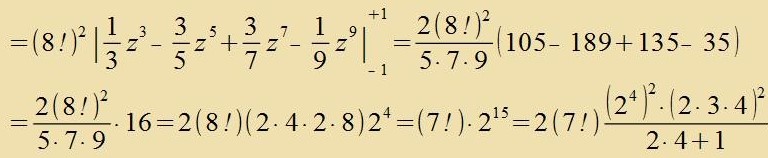		Dis Ergebnis ctimmt ebenfalls mit Gleixung (30) überein

Das Ergebnis ist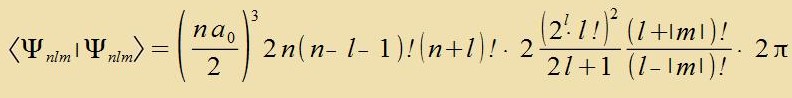

Mit der Vurtsel aus dem Kervert als Normirungsfaktor erhält man di normirte Vellenfunktsion des Elektrons imm Vasserctoffatom. Datsu kommt nox ein Fazenfaktor e^iβ mit belibigen reellen β, der vegen (e^iβ)*∙e^iβ=1 keine Ausvirkung auf den Normirungsfaktor hat.

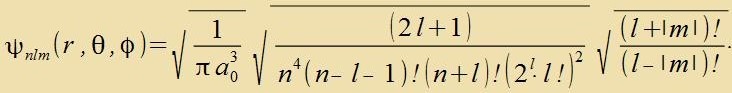
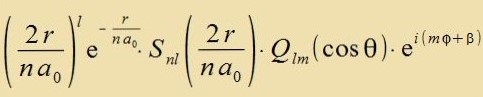
mit den Polünomen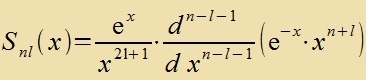

unt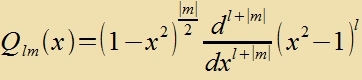

Tsurük tsu Kapitel XXVII. Vellenmexanik