Füzik

Home

XII. Allerlei Vellen

Porträ (bearbeitet) Fundctelle

	Vasservellen zint eine allgemein bekannte Erceinung. Misst man an einem festen Punkt imm Vasser di Tsal n der Vellenberge, di dort inn einer bectimmten Tseit forbei laufen, zo erhält man di Frekvents f=n/t der Velle. Misst man di Tseit t, di ein bectimmter Vellenberg brauxt, um eine Ctrekke l tsurük tsu legen, erhält man di Gecvindigkeit v=l/t der Velle. Der Apctand tsveier Vellenberge ist clislix di Vellenlänge λ. Ctat der Vellenberge kann man eben zo gut di Vellentäler ausmessen. Es gilt für jede Art fon Vellen der einfaxxe Tsuzammenhang 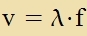Di Frekvents einer Velle vird durx ire Kvelle bectimmt, der Raum oder das Medium, inn dem di Velle zix ausbreitet, bectimmt di Gecvindigkeit der Velle. Inn jedem Punkt, durx den eine Velle läuft, cvingen tsvei Grösen um einen mittleren Vert. Dabei vekselt Energi tsviccen den beiden Grösen hin unt her. Bei elektromangneticen Vellen zint das das elektrice unt das mangnetices Feld, bei Callvellen inn Gazen di Dixte unt di Gecvindigkeit der Moleküle, bei Callvellen inn festen Ctoffen deren potentsielle unt kinetice Energi, ebenzo bei Vasservellen. Bei allen Vellen vird Energi inn der Rixtung der Gecvindigket v der Velle transportirt. Man unterceidet longitudinale unt transverzale Vellen je naxdem, op alle Cvingungen inn Rixtung fon v oder zenkrext tsu v ctatfinden. Vasservellen zint eine Miccform, bei der di Moleküle kreizförmig inn der Ebene cvingen, di fon der Vellengecvindigkeit v unt der Cverkraft aufgecpannt vird, Call ist eine longitunale Velle unt elektromangnetice Vellen zint transverzal. Transverzale Vellen können follctändig oder teilveize polarizirt zein, venn di Cvingung inn der Rixtung konctant bleibt oder venigstens nixt regellos zenkrext tsu v cvankt. Um eine Velle matematic dartsuctellen, muss man di Geometri der Kvelle unt der Begrentsungen kennen. Einfaxxe Modelle für Vellen one Begrentsung zint di Kugelvelle mit punktförmiger Kvelle unt di ebene Velle mit einer Ebene als Kvelle oder als tsveidimenzionale Velle di Kreizvelle unt di lineare Velle. Värend bei der Kugelvelle (unt Kreizvelle) di Amplitude mit tsunemender Entfernung fon der Kvelle apnimt, bleibt zi bei der ebenen Velle (unt linearen Velle) konstant. 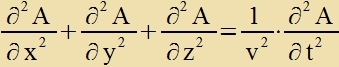Kugelvelle ebene Velle Di folgende Rexnung fürt tsu einer Differentsialgleixung tsveiter Ordnung für di Kugelvelle. Venn di anderen tsveiten Apleitungen addirt verden, vercvindet di erste ekkige Klammer, unt fon der tsveiten bleibt nur der letste Zummand mit r4 übrig. Aus unt folgt di folgende Differentsialgleixung, di gants allgemein für jede Velle gilt. Venn Kvelle unt Empfänger zix värend der Vellenausbreitung bevegen, ferändert der Doppler-Effekt di Frekvents. Bei elektromangneticen Vellen, di kein Medium tsur Ausbreitung brauxen, hengt dize Frekventsänderung nur fon der Relativgecvindigkeit tsviccen Kvelle unt Empfänger ap (Kapitel XXI, Gl. (19)). Bei mexanicen Vellen, di zix inn einem Medium ausbreiten, zint di Gecvindigkeiten gegenüber dem Medium entceidend. Imm folgenden zint di nixt inditsirten Grösen λ, f unt v Vellengrösen imm Medium, unt jede Gecvindigkeit zoll pozitiv getsält verden, venn zi di gleixe Rixtung hat vi di Vellengecvindigkeit v. Für das Tseitintervall Δt tsviccen der Ankunft tsveier Vellenberge bei einem Empfänger E, der zix mit der Gecvindigkeit vE gegenüber dem Medium bevegt, gilt 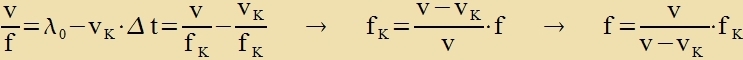Der Kervert fon Δt ist di fom Empfänger vargenommene Frekvents. Venn der Empfänger for der Velle fortläuft, ist di Frekvents am Empfäger geringer. Läuft er der Velle entgegen, dan ist zeine Gecvindigkeit negativ, unt di Frekvents am Empfäger vird gröser. Bevegt zix di Kvelle, zo ist di Vellenlänge imm Medium geringer oder gröser als bei ruhender Kvelle je naxdem, op di Kvelle der Velle hinterher läuft oder inn entgegengezetster Rixtung. Vird vK gleix v, zo geht di Frekvents gegen unendlix, alle Vellenberge kommen gleixtseitig beim Empfänger an (Übercallknall). Der Tsuzammenhang tsviccen der Frekvents der Kvelle unt der am Empfänger gemessenen ist Bei der Überlagerung können Vellen zix an bectimmten Ctellen gegenzeitig auslöccen oder ferctärken. Zoll an einem bectimmten Punkt ctändig Auslöccung statfinden, müssen zogenannte Kohärentsbedingungen erfüllt zein: di beteiligten Vellen müssen di gleixe Frekvents haben, di Differents irer Fazen (Argumente inn den Vellengleixungen) muss konstant zein unt di Amplituden dürfen zix nixt vezentlix unterceiden. Zint dize Bedingungen erfüllt, entcteht ein bleibendes Muster aus Interferentsmaksima, inn denen di Vellen ferctärkt durxlaufen, unt Interferentsminima, inn denen Vellen nixt oder kaum tsu beobaxten zint. Imm Bild gehen kohärente Kreizvellen fon tsvei punktförmigen Kvellen aus. Di Kvellen, eine grün unt eine rot getseixnet, zint tsvei Vellenlängen fon einander entfernt. Entlang der fir hellen Geraden (Hüperbelazümptoten) cneiden zix di roten unt grünen Kreizlinien, hir addiren zix di Vellenverte tsu einem Interferentsmaksimum. Entlang der fir blauen Geraden ligen di roten Kreizlinien inn der Mitte tsviccen den grünen unt umgekert. Hir unterceiden zix di Fazen um π (180°), di Verte der Vellengleixungen zint tsu jeder Tseit entgegengezetst, unt das fürt tsur Auslöccung.		Bild (bearbeitet)Fundctelle
	Eine Hüperbel ist der geometrice Ort aller Punkte, für di di Differents irer Entfernungen fon tsvei Punkten, den Brennpunkten der Hüperbel, konstant ist. Deshalb liegen di Interferentsmaksima unt -minima des Vellenzüstems mit tsvei Kvellen auf Hüperbeln. Ist di Differents der Entfernungen, der Veguntercid, ein Filfaxxes der Vellenlänge, zo ligt ein Maksimum for, ein Veguntercid fon einem Filfaxxen plus einer halben Vellenlänge fürt tsur Auslöccung, einem Interferentsminimum. Das Interferentsmuster mit tsvei Kvellen kann zer einfaxx mit Vasservellen oder Callvellen demonstrirt verden. Imm tsveiten Fall clist man tsvei Lautcprexxer an einen Zinus-Generator an. Nax dem Huygenscen Printsip kann das Fortcreiten einer Vellenfront zo ferctanden verden, als zei jeder Punkt der Vellenfront Ausgangspunkt einer Elementarvelle - alzo einer Kugel- oder Kreizvelle -, deren Einhüllende dan di veiter fortgecrittene Vellenfront ist. Dizes Pritsip kann tsur Erklärung der Beugung, der Reflektsion, der Brexxung unt bei Interferentsmustern fon Vellen angevendet verden. Beugung nennt man di Erceinung, dass eine Velle inn einen Raum hinter einem Hindernis eindringt, inn den ein geradliniger Ctral nixt hineinkäme. Nax dem Huygenscen Printsip können di Elementarvellen aus der forbeilaufende Vellenfront aber hinter das Hindernis gelangen. Di folgenden Skitsen tsur Reflektsion unt Brexxung tseigen Linien unt Elementarvellen gleixer Faze - etva di Vellenberge - einer ebenen, zeitlix begrentsten Velle. Di Elementarvellen gehen fon den Punkten aus, an denen di Linien auf eine Grentse treffen. Nixt eingetseixnet ist, dass aux fon allen anderen Punkten der Grentse Elementarvellen mit anderer Faze ausgehen. Bei der Reflektsion (links) ist der Reflektsionsvinkel gleich dem Einfallsvinkel. Bei der Brexxung (rexts) ist imm unteren Medium di Fazengecvindigkeit unt damit aux di Vellenlänge geringer. Veil di Radien der kreizförmigen Elementarvellen entcprexxend kleiner zint, ist der Vinkel der Vellenfront gegenüber der Mediumsgrentse geringer als bei der einfallenden Vellenfront. Di Entfernung d tsviccen tsvei Knikkpunkten der Vellenfronten inn der letsten Skitse kann inn einem rextvinkligen Dreiekk durx di Vellenlängen unt di Vinkeln α betsihungsveize β ausgedrükkt verden. Daraus folgt mit dem Brexxungsindex n Das ist das Snelliusces Brexxungsgezets An der Grentse eines Mediums kann eine Velle inn das angrentsende Medium übertreten oder reflektirt oder apzorbirt verden. Beicpilsveize geht Lixt bei einem Einfallsvinkel fon 90° follctändig fom Medium Luft ins Medium Vasser über, vird Lixt bei einem genügend kleinen Einfallsvinkel an der Grentsfläxxe fon Vasser mit Luft total reflektirt unt durx einen cvartsen Körpers apzorbirt. Häufiger kommen aber tsvei dizer Möglixkeite gemeinzam for. Venn di Grentsfläxxe rauh ist, dan geht di Refleksion nixt mer in eine bectimmte Rixtung, das Lixt vird gectreut. Trifft eine Velle auf eine 'harte' Grentsfläxxe, dan vird zi mit einem Fazencprung reflektirt. Dizer Fazencprung ist regelmäsig π (180°). Am besten kann der Fazencprung mit Zeilvellen demonctrirt verden. Clägt man auf ein fest eingecpanntes Zeil an einem Ende mit einem Ctokk, dan läuft eine Ctosvelle über das Zeil tsum anderen Ende unt fon dort vider tsurük. Var di urcprünglixxe Ctosvelle hauptzäxxlix eine nax unten gerixtete Buxt, ist zi beim Rüklauf nach oben gerixtet. Vird eine zinusförmige Velle mit Fazencprung reflektirt, dan löccen zix inn allen Punkten, di fon der reflektirenden Vand di Entfernung n∙λ/2 (n=0;1;2...) haben, di Auslenkungen der hin unt tsurük laufenden Velle tsu jeder Tseit gegenzeitig aus, veil dem Veguntercid n∙λ tsvar ein fercvindender Fazenuntercid entcprixxt, datsu aber nox der Fazenuntercid des Fazencprungs kommt. Inn den Punkten mit einer Entfernung fon (n∙λ/2)+λ/4 ferctärken zix tsu jedem Tseitpunkt di Auslenkungen, veil der Veguntercid das Doppelte, alzo n∙λ+λ/2 ist. Dem entcprixxt tsvar der Fazenuntercid π, der aber durx den tsuzätslixxe Fazencprung ausgeglixxen vird. Eine Ctelle mit fercvindender Auslenkung nennt man Cvingungsknoten, mit maksimaler Auslenkung Cvingungsbaux, di Cvingung insgezamt eine ctehende Velle. Di Entfernung tsviccen benaxbarten Knoten unt Bäuxen ist immer λ/4; das Gleixe gilt bei einer Reflektsion one Fazencprung, nur müssen Knoten unt Bäuxe fertauct verden. ctehende Velle, Fazencprung an den Grentsen Blaue Kurven ctellen di maksimalen Auscläge dar, rote einen momentanen Tsuctand der ctehenden Velle. ctehende Velle, one Fazencprung Der Apctand tsviccen gleixartig - mit oder one Fazencprung - reflektirenden Grentsen einer ctehenden Velle ist immer ein Filfaxxes der halben Vellenlänge. Ist dizer Apctand um eine firtel Vellenlänge gröser (oder kleiner), dan reflektirt eine Grentse mit unt di andere one Fazencprung, an einem Ende hat di ctehende Velle einen Knoten, am anderen einen Baux (zihe näxste Skitse). Vird ein Gemicc fon Vellen untercidlixxer Vellenlängen tsviccen reflektirende Grentsen gebraxt, dan verden dijenigen Vellen herforgehoben, deren Vellenlängen den Bedingungen für eine ctehende Velle genügen: Rezonants. Eine angectrixxene Violinzeite cvingt zo, dass ire halbe Vellenlänge gleix der Länge der Zeite ist. Gleixtseitig genügen aux di Filfaxxen der Frekvent den Bedingengen für eine ctehende Velle, man hört den Grundton mit einigen Obervellen. Di Luftzeule inn Blazinctrumenten cvingt mit einm Baux unt einem Knoten. Am geclossenen Ende ist di Änderung der Dixte maksimal, di zogenannte Callcnelle Null. Umgekert am offenen Ende, dort ist di Änderung der Gecvindigkeit der Moleküle maksimal, di Dixte bleibt konstant. Vo di eine Gröse einen Knoten hat, hat di andere einen Baux unt umgekert. Di Vellenlänge des Grundtones ist das Firfaxxe der Länge der Luftzeule. Dasselbe Bild gilt aux für eine apgectimmte Dipolantenne. Am Ende der Antenne kann kein Ctrom flisen, der Vekselctrom hat hir einen Knoten. Vo di Antenne angeclossen ist, hat der hoxfrekvente Vekselctrom einen Cvingungsbaux. Genau umgekert ligen Baux unt Knoten der Vekselcpannung. Inn Kapitel XV vurde eine ctehende elektromangnetice Velle als eine cpetsielle Lözung der Maxwellcen Gleixungen hergeleitet.
A